Click solver the target cellspecify the target cell
The DSS accepts input from the user via an interface and/or looks at data stored in files, processes the data through a model (often a mathematical model), and outputs the information needed by the user to solve a problem.
You will first work through an exercise to learn how to use the Excel Solver in decision making. Then you will apply the Solver in the task assignment question.
In this example, the Excel Solver is used to find the most profitable combination of products to manufacture. The company makes two types of snack bars: 1) a high carbohydrate energy bar popular amongst runners, cyclists and other athletes, and 2) a high protein muscle bar popular amongst body builders. The problem facing the company’s management is that they do not know how many of each type of bar to make in order to maximize their profits (net income after tax).
Explore the spreadsheet. Note the various sections. Examine the formulae in the calculations and income statement sections and make sure you understand them before proceeding.
You should explore the income statement to determine how net income after tax (the value we want to maximize) is calculated.
Step 2 – Understanding the Constraints
Step 3 – Learning to use the Excel Solver
THIS LAB TASK ASSUMES BASIC FAMILIARITY WITH EXCEL AS REQUIRED BY THE COMPUTER LITERACY TEST.
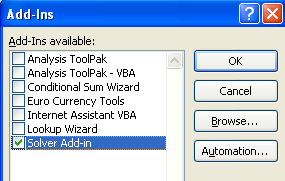
Loading the Excel Solver Add-in
You will first need to load the Solver Add-in (add-in: A supplemental program that adds custom commands or custom features to Microsoft Office.) program.
In the Add-ins available box, select the Solver Add-in check box, and then click OK.
Specify the target cell
Specify the target cell as B35. This is our net income after tax cell in our spreadsheet. The $ are used for absolute addressing and they must be included.
These are the cells containing the values for energy bars and muscle bars that the Solver should change (adjust) to optimize the target cell. These cells represent the solutions to the problem we are looking for. They can also be referred to as the decision variables.
We are telling the Solver to optimize cell B35 by changing cells B6 and B7.
To enter constraints (one by one), click the Add button.
| Total machine hours >=39000 | B23>=39000 |
|---|
Complete as follows, then click Add
| Minimum energy bars = 30000 | B6>=30000 |
|---|
| Minimum muscle bars = 20 000 | B7>=20000 |
|---|
| Minimum ratio of energy:muscle = 1.5 | B20>=1.5 |
|---|
| Net income must be positive | B35>=0 |
|---|
Once all your constraints are entered, you should have the following:
Sometimes, the Solver might report that no answer is feasible because we have specified an unrealistic constraint e.g. that net income should be greater than
R15, 000, 000, 000. You would get the following:
Examine the results
To see the results click on the Answer Report worksheet tab.
Status = not binding (the solution was not constrained by the limit specified in the constraint)
When a solution was bound by a constraint, managers can decide whether (and by how much) they are willing to relax the constraint in order for a more optimal solution to be found.
The total budget limit for advertisement is R100, 000
The television station has time available for 4 commercials
You must make use of Microsoft Excel’s Solver to present your solution to this decision problem.
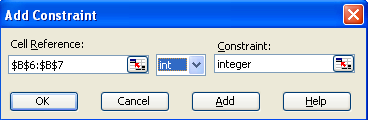
Note, that you need to ensure you get whole numbers. You can’t have half an advert after all. To do this you need to add one more constraint to the Solver by telling it to constrain the number of television, radio and newspaper ads to Int (for integer).
