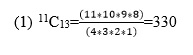Combination Homework Help
Introduction to Combination
A Combination is an arrangement of items in which order does not matter. To find the number of Combinations of n items chosen r at a time, you can use the formula
nCr = n!/r!(n-r)! where 0 ≤ r ≤ n
Example for Combination
A class consists of 14 boys and 17 girls. Four students from the class are to be selected to go on a trip.
(a) How many different possibilities are there for the 4 students selected to make the trip?
(b) If it has been decided that 2 boys and 2 girls will make the trip, then in how many different ways could the 4 students be selected?
Solution
(a) C(31,4) = = 31,465
(b) C(14,2) ! C(17,2) = 91 ! 136 = 12,376
Number of combinations: The number of all combination of n things, taken r at a time is:
nCr=n!/R!(n-1)! = (n(n-1)(n-2)….to r factors)/r!
An Important Result:
nCr=1 and nCr = nC(n-r)
Example: