And only the compound propositionp tautology

https://amyglen.wordpress.com

LECTURE 25

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 25	1

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 25	2

Recall: Logical Arguments/Inferences

Usual form: (H1 · H2 · · · · · Hn) ∆ C
A logical argument (or inference) asserts that the conjunction of n hypotheses H1, H2,

)	C

Otherwise the inference is said to be invalid or a fallacy.

Chapter 7: Propositional Logic		4

Some valid inferences tend to arise very frequently, and it is convenient to use them over and over again instead of having to draw up a truth table each time we use them.

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 25	4

If I study, then I will not fail mathematics.

If I do not use online social networking site(s), then I will study. But I failed mathematics.

Dr Amy Glen (Murdoch University)	s				Lecture 25	5
	¬n f
	)	n
	MAS162 – Foundations of Discrete Mathematics

Thus the logical implication

[(s æ ¬f) · (¬n æ s) · f] ∆ n

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 25	6

is a tautology.

I But using the rules of inference takes some getting used to, and some students are frightened into always doing a truth table.

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 25	7

Write the following argument in symbolic form & prove that it is logically valid.

I become weak if I do not eat meat.

h · [(w ‚ ¬i) æ ¬h]

∆ ¬(w ‚ ¬i)

∆ ¬(¬m)

… m . . . (4)

(modus tollens) H4 · H3

(de Morgan + double negation)

(simplification)

(2) · H1
(modus tollens)

(double negation)

(4) · (5)

Chapter 7: Propositional Logic		10

P := (H1 · H2 · · · · · Hn) æ C
is a tautology, i.e., the conclusion C is true whenever all of the hypothesis H1, H2, . . . , Hn are true.

I So we can always determine the validity or otherwise of an inference simply by computing a truth table.

I Suppose you were not told in advance that a given inference is valid, but instead were asked to determine its validity.

I How would you go about doing this without computing the truth table?

Chapter 7: Propositional Logic	Testing Validity of Inferences	12

I Remember that we are trying to discover whether the compound proposition
P := (H1 · H2 · · · · · Hn) æ C
is a tautology or not.

I On the other hand, if we fail to find the assignment of values, then we know that P must be a tautology, and so we can set about proving it.

Chapter 7: Propositional Logic		14

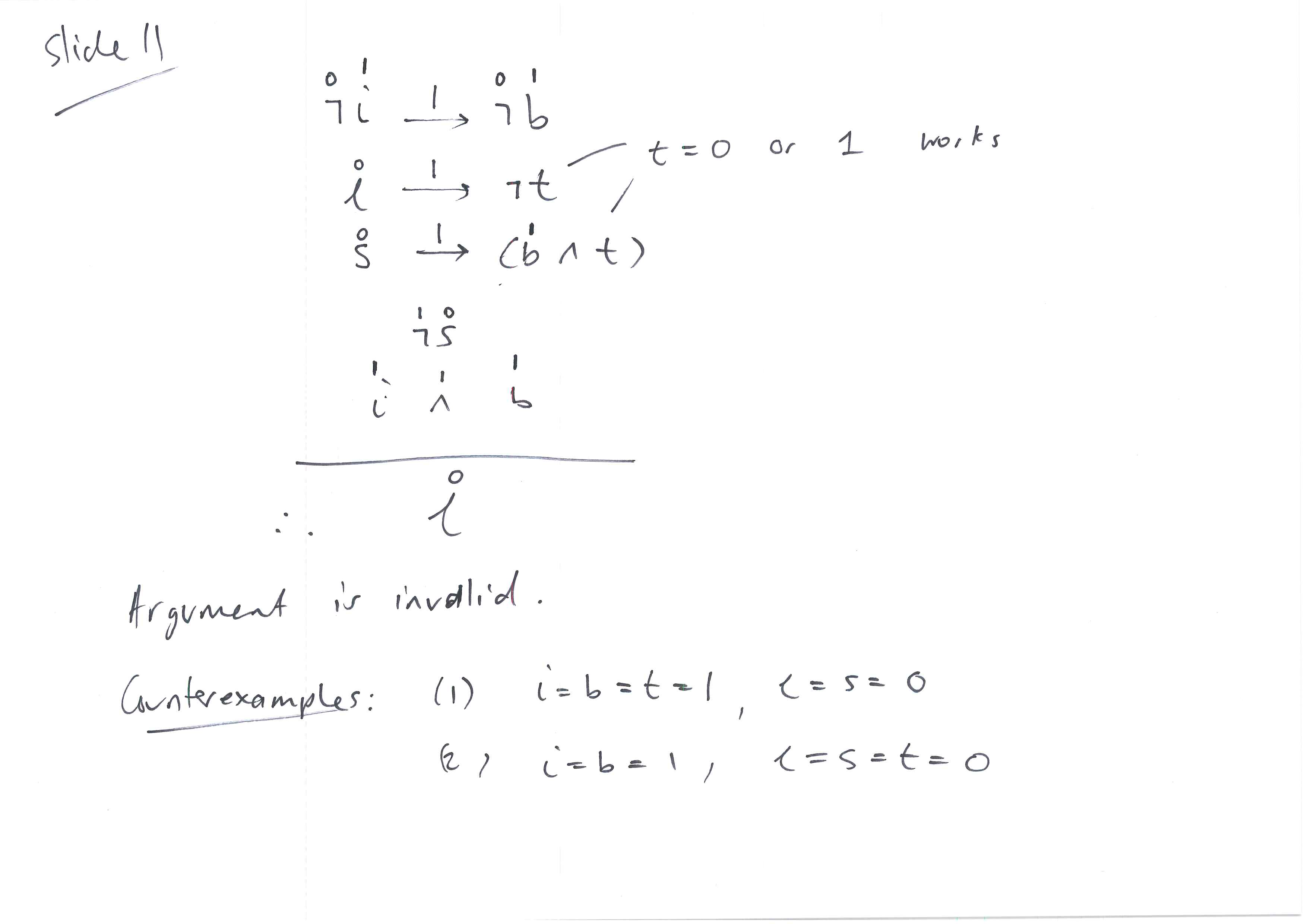
Example

		¬i ¸	æ æ æ
		s

			·	b
	)	¸			14
Dr Amy Glen (Murdoch University)					14

Solution

So the inference is invalid, and a counterexample is i = b = t = 1 and¸ = s = 0.

Chapter 7: Propositional Logic	Testing Validity of Inferences	16

		Lecture 25	16
Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 25	16

Setting out your work

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 25	18

Slides 8-9 (cont.)

Slide 15