And then findingthe distance sin sin coscos
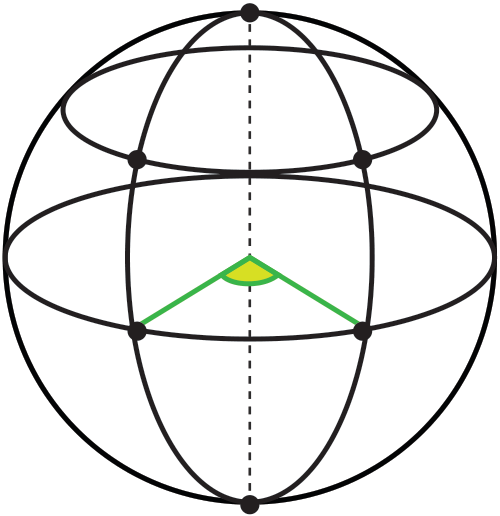
Spherical Geometry
11 &12
Illustrations and web design: Catherine Tan
© VCAA and The University of Melbourne on behalf of AMSI 2015.

Spherical Geometry
• Familiarity with circle geometry.
Motivation
• How does a spherical model of the Earth help me to understand the different time zones that have been established ?
Content
A guide for teachers – Years 11 and 12 • {5}
For the purposes of modelling key aspects of travel and time on the Earth, for a course such as Further Mathematics in the Victorian Certificate of Education, treating the Earth as a true sphere with a radius of 6 400 kilometres will provide reasonable answers from a conceptually simple framework.
| • |
|
|
|---|---|---|
| diameter | ||
O B
| A | minor arc | |
|---|---|---|
|
two arcs are called semicircles. Other-
wise, one arc is longer than the other. The
| A |
|
|---|
A chord AB of a circle divides the circle into
two segments. The two segments are called
a major segment (the larger one) and a mi- BCalculation Notes
Unless it is specifically requested, the π value obtained by accessing the appropriate function in a scientific or graphic calculator should be used in any calculation involv-ing π.
|
the length of the arc | |||||
|---|---|---|---|---|---|---|
| circumference | = | |||||
| so | ||||||
| ∴ l = | ||||||
| = |
|
|||||
|
||||||
Solution
|
|---|
{8} • Spherical Geometry AMSI module
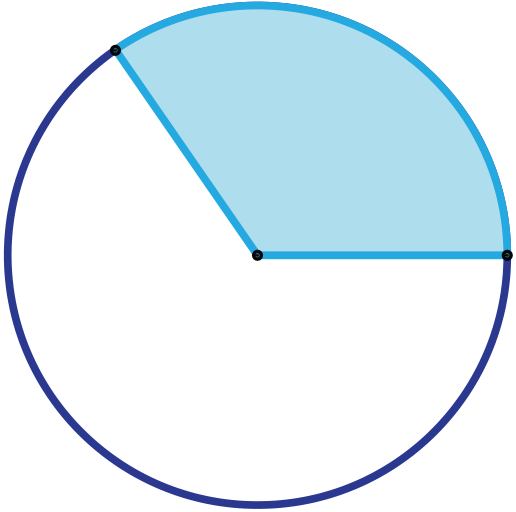
Sector
The area of a sector depends not
of a sec quare m A = |
||
Areas of segments
Where a chord subtends an angle θ at the r centre of a circle of radius r, the area of the
or rewritten as
|
� |
|
||
Example
Find the area, correct to two decimal places, of the minor segment in a circle of radius
{10} • Spherical Geometry AMSI module
Example
| � 2πθ 360◦ −sinθ | � | =1 2×152 | �2×π×60◦ | −sin60◦ | � |
|---|
Example
Find the area, correct to two decimal places, of the minor segment in a circle, of radius 13 cm where the chord length is 21 cm.
| −sin107.74◦ |
|---|
= 78.409...
≈ 78.41 cm2
|
A | |
|---|---|---|
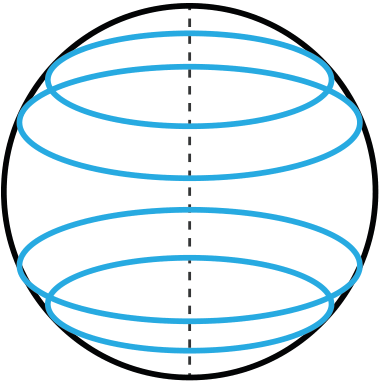
Latitude
Latitude is a measure of the position of a point on the
earth’s surface in terms of degrees north or south of a
baseline - the equator. These values vary from 90◦S
to 90◦N. The latitude of the Equator is 0◦. angle of latitudeEvery plane perpendicular (at right angles) to the earth’s axis cuts the surface of the earth in a circle called a parallel of latitude.
Latitude is determined by measuring the angle of elevation of the sun at noon, and adding or subtracting an allowance for the time of year. Using the angle only is cor-rect for just two days of the year - the spring and autumnal equinoxes. In midwinter we need to subtract 23.45◦and at midsummer we need to add 23.45◦. These allowances are due to the fact that the earth is tilted at this angle as it orbits the sun. Books of correc-tion factors for every day of the year (almanacs) were used for many years until global positioning satellites were used.
Longitude
Longitude varies from 180◦W of Greenwich to 180◦E of Greenwich.
The two meridians on a particular great circle will have values which sum to 180◦, but one will have a designation W and the other a designation E. For example, 60◦W is on the same great circle as 120◦E.
One involved measuring the lunar distance - the angle between the Moon and another celestial object (a star or the sun) - which would lead to determination of the position of the measurer through calculation based on reference values. This method required the compilation of tables of reference values (an almanac) for every day of every year well in advance of their required use - a task which required a lot of human calculating time in a pre-electronic computer era.
The second, and simpler, method involved taking a chronometer, which could keep very accurate time at sea, and calculate position almost immediately by comparing the chronome-ter time for the fixed reference point with local time. It took until the 1850’s to build accurate chronometers cheap enough for their widespread use.


{14} • Spherical Geometry AMSI module
| G | N |
|---|
| S |
|---|
Paris (France) is at 48.67◦N and 2.33◦E. How far is it from Paris to the North Pole and the Equator travelling along the meridian, correct to the nearest km ?
Solution
Note: The metre was originally defined as one ten-millionth of the distance from the
Each meridian is a great circle, with a radius of 6400 km.
From Melbourne to the Equator
≈ 4225 km
From Melbourne to the South Pole The angle between the latitude of Melbourne and the South Pole is 90.00◦−37.82◦= 52.18◦
|
|---|
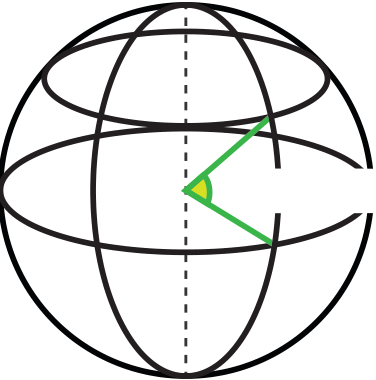
Finding the distance between two places on the surface of the Earth implies finding ei-ther the great circle distance (the shortest distance between any two points on the sur-face of a sphere) or the small circle distance (travelling along a parallel of latitude). To complete these calculations, we need to know the location (latitude and longitude) of each place.
There are four types of calculations that can be performed for this kind of problem.
The first two are part of the Further Mathematics course, and the third is a reasonable extension of this, and so the first three will be covered below. The fourth is not part of the Further Mathematics course, but will be covered in the Extension Activity at the end of these notes.
A guide for teachers – Years 11 and 12 • {17}
Each meridian is a great circle, with a radius of 6400 km. The angle between the latitude of Torrens Creek and that of Kyabram is 36.32◦- 20.77◦= 15.55◦.
(We find the difference since both places are on the same side of the Equator!)
≈ 1737 km
Example
{18} • Spherical Geometry AMSI module
Solution
Each meridian is a great circle, with a radius of 6400 km. The angle between the latitudeof Broken Hill and that of Morioka is 31.95◦+ 39.70◦= 71.65◦.
= 8003.31...
≈ 8003 km
A guide for teachers – Years 11 and 12 • {19}
|
|---|
Example
From Perth to Baoding
{20} • Spherical Geometry AMSI module
Distance between places on the Equator
Solution
The Equator is a great circle, with a radius of 6400 km. The angle between the longitude of Libreville and that of Kismanyo is 42.32◦? 9.27◦= 33.05◦.(We find the difference since both places have the same longitude direction (E))
Example
We could also find the angle between these two places by recognising that both are close to 180◦E/W. We could find the angle between the Galapagos Islands and 180◦E/W, the
|
|---|
{22} • Spherical Geometry AMSI module
In the right-angle triangle shown right, thehypotenuse is the radius of the Earth (6400
33.5°
For the small circle, radius small circle
From Sydney to Margaret River
| l =rπ 180◦ ×θ = 5337π 180◦ ×36.09◦ = 3361.719... ≈ 3362 km |
|---|
Example
From Hamilton to Orbost
Example
| Both Sydney (Australia) and Cape Town (South Africa) are on the 33.5◦S parallel of lat- |
|---|
|
|---|
Great circle distance between places with the same latitude
Finding the great circle distance between two places on the same latitude takes advan-tage of the fact that both places are on the circumference of the same small circle.
Both Sydney (Australia) and Cape Town (South Africa) are on the 33.5◦S parallel of lat-itude, but Sydney is at 151.13◦E whereas Cape Town is at 18.22◦E How far is it from Sydney to Cape Town travelling the great circle route, correct to the nearest km ?
Solution
Angle between earth radii
| θ = cos−1 | �64002 +64002 −97852 2×6400×6400 |
|
O | |
|---|---|---|---|---|
| 6400 km | ||||
| 9785 km | ||||
| A | B | |||
Example
Both Launceston (Tasmania, Australia) and Puerto Monti (Chile, South America) are on the 41.3◦S parallel of latitude, but Launceston is at 147.08◦E whereas Puerto Monti is at 72.57◦W. How far is it from Launceston to Puerto Monti travelling the great circle route, correct to the nearest km ?
The angle between the longitude of Launceston and that of Puerto Monti is 147.08◦+ 72.57◦= 219.65◦. We find the sum since these places are on different sides of the Prime Meridian, but this is the major arc, and the minor arc will be 360◦−219.65◦= 140.35◦.
Angle between earth radii
OS
4808 km 4808 km
140.35°
d
A B
| θ = cos−1 | �64002 +64002 −90462 2×6400×6400 | � | ||
|---|---|---|---|---|
| O | ||||
|
||||
| = 10046.394... |
|
|||
| A | B | |||
Greenwich Mean Time (GMT) was established at the Royal Observatory at Greenwich (just outside of London) in 1675 to assist mariners in calculating their longitude at sea. This was at a time when every town and city in England kept its own time, based on the local noon. These differences became a problem when railway networks were built across the country. The English railway companies were the first to adopt a standard time in the 1840’s, based on GMT and managed with portable chronometers, but GMT did not become the standard time for the whole of England until 1880.
New Zealand, at the time a British colony, was the first country to adopt a standard ref-
Example
A direct flight from Melbourne to Perth leaves Melbourne at 5.00 pm local time and ar-rives in Perth at 7.10 pm local time. If Melbourne is on the 145◦E meridian and Perth is on the 115◦E meridian, calculate the total journey time.
Example
The Australian Cricket team is flying from Perth to Johannesburg (South Africa) for a series of matches. Their flight leaves Perth at 6.05 am (local time) and arrives in Johan-nesburg at 8.50 pm (local time). If Perth is on the 115◦E meridian and Johannesburg is on the 28◦E meridian, calculate the total journey time.
Example
Australian Eastern Standard Time (which includes Melbourne and Sydney) is based on the 150◦E meridian and New York (USA) time is based on the 75◦W meridian. If a flight leaves Melbourne at 10.30 am and arrives in New York at 10.15 pm on the same day, calculate the total journey time.
Total journey time = 10.15 pm−10.30 am+15 hours = 11 hr 45 min+15 hours
= 26 hours 45 min.Example
Time difference due to longitude =150◦÷15◦= 10 hours
Total journey time = 4.45 am−2.20 pm+10 hours
= 14 hr 25 min+10 hours
= 24 hours 25 min.
Example
A large pond in the shape of a hemisphere has a radius of 5 m and it is planned to fill the pond so that the water in the centre of the pond is 2 m deep. The pond’s builders then want to attach a metal ring around the waterline which will be used to hold a cover for the pond in the winter months.
= 5−2
|
A | B |
|---|
The area of the cover will be 50.27 square metres.
Extension Activity
The simplest method is based on the "Spherical Law of Cosines" which is a method for finding distances on the surface of a sphere. It can have difficulties calculating distances between two places that are very close together (less than 10 metres), but this is not really a practical calculation.
A more complex method, based on the "haversine" calculation method, forms the basis of a number of web-based processes for performing these calculations. It is accurate for most distances on a sphere, but has difficulties with "antipodal points" which are points at each end of a diameter .
To carry out the calculation we require the latitude and longitude values for the two places concerned.
Following the terminology used in the development of this formulation, latitudes (North) and longitudes (East) are given positive values, and latitudes (South) and longitudes (West) are given negative values.
To clearly demonstrate why the sign applied to an angle is important, we will break the following example calculation into two parts, finding the cos value (D) first using sine and cosine values rounded to four decimal places, and then finding the distance (d).
Example
|
|---|
We can see from the details of this calculation that the signs allocated to each latitude value have a major impact on the calculation of the angle between the radii leading to the two places. The negative value for cosine leads to an obtuse angle, fairly reflecting the distance between the two places chosen.
Example
|
|---|
|
|---|
| d =6400×π |
|
|---|
Giving θ =11139×180◦
θ = 99.72◦