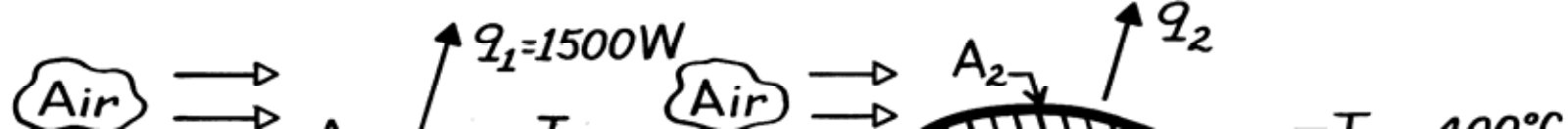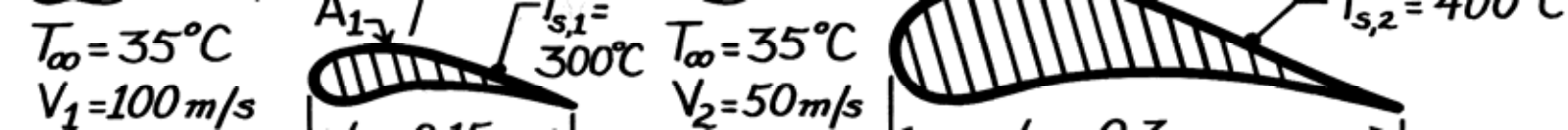Blade shapes are geometrically similar for prescribed geometry
The Reynolds numbers for the blades are
| Re | L,1 | = | ( | V L / 1 1 ν ) | = | 15/ Re | L,2 | = | ( | = | 15/ . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Re | L,1 | = | Re | L,2 | . | Also, Pr 1 | = | Pr . 2 | |||||||||||||
h 2 =
|
− | T∞ | ) |
|
|||||||||||||||||
Hence, the heat rate for the second blade is
| q | = | h A 2 | ( | T s,2 | − | T∞ | ) | = | T∞ | ) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2 |
|
T∞ | ) |
|
||||||||||||||
| q | = | T s,2 | − | T∞ | q 1 | = | ( | 400 | |||||||||||
| − | 35 | ||||||||||||||||||
| 2 | T s,1 | − | T∞ | ( | 300 | − | 35 | < | |||||||||||
| q | 2 | = | |||||||||||||||||