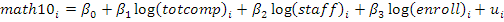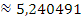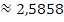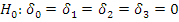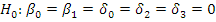But the remaining gauss-markov assumptions hold
•For each question, there is one and only one correct answer.
•A correct answer is worth 1 point; an incorrect answer shall be attributed 0 points.
Dependent Variable: MATH10
Method: Least Squares
Sample:
Included observations:
| Coefficient | Std. Error | t-Statistic | |||||
| C | -207.6649 | ||||||
| LTOTCOMP | 21.15500 |
|
|
||||
| LSTAFF | 3.980021 | ||||||
| LENROLL | -1.268047 |
|
|
||||
| 0.065378 Mean dependent var | |||||||
|
|
||||||
| 10.18239 Akaike info criterion | |||||||
|
|||||||
|
-1523.746 Hannan-Quinn criter. | ||||||
| 9.420035 Durbin-Watson stat | |||||||
| Prob(F-statistic) | |||||||
|
|||||||
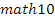 |
|
||||||
(which represents school size).
1
sign
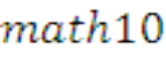 with respect to with respect to |
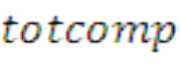 and it bears the and it bears the |
|---|
b)All
| c) | 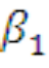 Just Just |
|---|
salary, in dollars), was omitted from this model. Knowing that:
, which Gauss-Markov assumptions are being
d)Zero Conditional Mean
e)No Perfect Collinearity
5. About this regression, it is also known the following Coefficient Variance-
Covariance matrix:
c)
d)
6. Now consider the following output:
Dependent Variable: MATH10
| Coefficient | Std. Error | t-Statistic | ||||
| C | -168.3782 |
|
|
|||
| LTOTCOMP |
|
|||||
| LSTAFF+LENROLL | -1.196471 |
|
||||
| R-squared | ||||||
| Adjusted R-squared |
|
|
||||
| S.E. of regression | ||||||
| Sum squared resid | ||||||
| Log likelihood |
|
|
||||
| F-statistic | ||||||
| Prob(F-statistic) | ||||||
|
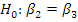 |
|||||
but using a different test statistic, given the information presented in this output?
d)No, because we still would need the coefficient variance-covariance matrix to
compute any type of test statistic
variable equal to one if a person is unemployed and zero otherwise. The
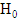 |
|
|---|
the 5% significance level becomes wider than the one above and so 1,7 will be
the 5% significance level becomes thinner than the one above and so 1,7 will be
outside the confidence interval
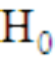 |
|---|
interval
e)None of the above
8. Consider a multiple linear regression model for cross-sectional data that analyses
Collinearity Assumption is not violated in this model as long as:
a)The sum of the three dummy variables is not equal to 1 across all observations
football clubs
e)Both a) and d) are correct
Suppose that when you decided to regress the model, the variable
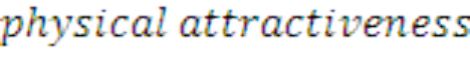 was not included. Then,
assuming that the correlation
was not included. Then,
assuming that the correlation
b)Positive, because
and Correlation(
,
)<0
5
long as we assume that the correlation between 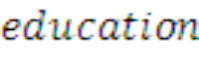 and
and
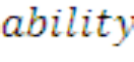 is zero
is zero
e)Negative, because
and Correlation(
,
)<0, as
where
is a gender dummy equal to 1 if female and zero otherwise, and
equals 1 if Portuguese and zero otherwise.
c)
d)
a)The Residual sum of squares of the restricted model is large relative to that of
the unrestricted model
e)Both a) and d) above are correct
f)Both c) and d) above are correct
a)You cannot perform such test because only the t-test is valid in large samples b)You cannot use the usual F test for multiple exclusion restrictions
c)You can use the usual F test for multiple exclusion restrictions
d)You can only use the LM test for multiple exclusion restrictions
e)You can use the LM test for multiple exclusion restrictions
f)Both b) and d) above are correct
g)both c) and e) above are correct
h)b) and e) above are correct
13. Consider a multiple linear regression model for cross-sectional data. If the Gauss-Markov assumptions hold, then:
a)Ds The OLS estimator will be consistent and unbiased
b)We can only guarantee the OLS estimator is unbiased
c)The OLS estimator is consistent only if the sample size is very large
d)The OLS estimator will be biased
e)Both b) and c) above are correct
f)Both c) and d) above are correct
g)Both a) and d) above are correct14. If under certain assumptions the OLS estimator is BLUE, Best Linear Unbiased Estimator, then we can conclude that it is:
a)the minimum variance unbiased estimator
b)an unbiased estimator
c)a linear estimator
d)an estimator
e)both b), c) and d) above are NOT correct
f)both b), c) and d) above are correct
16. Consider a multiple linear regression model where the Zero Conditional Mean assumption fails, but the remaining Gauss-Markov assumptions hold. Specifically, suppose E[u|X]=δ, where u is the vector of error terms, X is the matrix of regressors and δ has at least one element different than zero. What can you say about the bias (E[ |X]-β) of the OLS estimator in this situation?
a)the OLS estimator is still BLUE
b)the bias equals (X´X)-1X´ δ
c)the bias is still zero, always
d)the bias equals X´X´ δ
e)the bias equals X´ δ
f)None of the answers above is correct
a)Any proportion between 25% and 75%
b)33%
c)50%
d)0%
e)100%
f)either 50% or 100%
g)none of the answers above is correct19. WLS stands for what in Econometrics?
Mark your answer with an X in the table below
Any answers outside the table will not be considered
| Question Nr. |
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| 1. |
|
||||||||
| 2. | |||||||||
| 3. | |||||||||
| 4. | X | ||||||||
| 5. | |||||||||
| 6. | |||||||||
| 7. |
|
|
|||||||
| 8. | |||||||||
| 9. | |||||||||
| 10. | |||||||||
| 11. |
|
||||||||
| 12. |
|
||||||||
| 13. | |||||||||
| 14. | |||||||||
| 15. | |||||||||
| 16. | |||||||||
| 17. |
|
||||||||
| 18. |
|
||||||||
| 19. | |||||||||
| 20. |