Entering variable isx minimum ratio and its row index
Exercise 25:
8x1 − 4x2 − 6x3 − 8x4 + x5 + 3x6 + S2= 24
12x1 + 5x2 − 9x3 + 6x4 − 9x5 + 8x6 + S3= 360
| R2(old) = | 24 | 8 | -4 | -6 | -8 | 1 | 3 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| R2(new)=R2(old)÷8 | 3 | 1 | -0.5 | -0.75 | -1 | 0.125 | 0.375 | 0 | 0 |
| R3(old) = | 360 | 12 | 5 | -9 | 6 | -9 | 8 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| R2(new) = | 3 | 1 | -0.5 | -0.75 | -1 | 0.125 | 0.375 | 0 | 0 |
| 12×R2(new) = | 36 | 12 | -6 | -9 | -12 | 1.5 | 4.5 | 0 | 0 |
| R3(new)=R3(old) - 12R2(new) | 324 | 0 | 11 | 0 | 18 | -10.5 | 3.5 | 0 | 1 |
Negative minimum Zj-Cj is -28M-4 and its column index is 4. So, the
entering variable is x4.
Minimum ratio is 10.8 and its row index is 1. So, the leaving basis
variable is A1.
∴ The pivot element is 10.
Entering =x4, Departing =A1, Key Element =10
R1(new) = R1(old)/ 10
| R1(old) = | 108 | 0 | 10 | 6 | 10 | 9.5 | -2.5 | 0 |
|---|---|---|---|---|---|---|---|---|
| R1(new)=R1(old)÷10 | 10.8 | 0 | 1 | 0.6 | 1 | 0.95 | -0.25 | 0 |
| R3(old) = | 324 | 0 | 11 | 0 | 18 | -10.5 | 3.5 | 1 |
|---|---|---|---|---|---|---|---|---|
| R1(new) = | 10.8 | 0 | 1 | 0.6 | 1 | 0.95 | -0.25 | 0 |
| 18×R1(new) = | 194.4 | 0 | 18 | 10.8 | 18 | 17.1 | -4.5 | 0 |
| R3(new)=R3(old) - 18R1(new) | 129.6 | 0 | -7 | -10.8 | 0 | -27.6 | 8 | 1 |
| R3(old) = | 129.6 | 0 | -7 | -10.8 | 0 | -27.6 | 8 |
|---|---|---|---|---|---|---|---|
| R3(new)=R3(old)÷8 | 16.2 | 0 | -0.875 | -1.35 | 0 | -3.45 | 1 |
R1(new) = R1(old)* 0.25 R3(new)
R2(new) = R2(old) - 0.125 R3(new)
| R2(old) = | 13.8 | 1 | 0.5 | -0.15 | 0 | 1.075 | 0.125 |
|---|---|---|---|---|---|---|---|
| R3(new) = | 16.2 | 0 | -0.875 | -1.35 | 0 | -3.45 | 1 |
| 0.125×R3(new) = | 2.025 | 0 | -0.1094 | -0.1687 | 0 | -0.4312 | 0.125 |
| R2(new)=R2(old) - 0.125R3(new) | 11.775 | 1 | 0.6094 | 0.0187 | 0 | 1.5062 | 0 |
| Iteration-5 | Cj | 1 | 2 | 3 | 3 | 2 | 1 | ||
| B | CB | XB | x1 | x2 | x3 | x4 | x5 | x6 | Min/Ratio XB/x3 |
| x4 | 3 | 14.166 | -0.0581 | 0.7459 | (0.2614) | 1 | 0 | 0 | 14.166/0.2614=54.1905→ |
| x5 | 2 | 7.8174 | 0.6639 | 0.4046 | 0.0124 | 0 | 1 | 0 | 7.8174/0.0124=628 |
| x6 | 1 | 43.1701 | 2.2905 | 0.5207 | -1.3071 | 0 | 0 | 1 | --- |
| Z=101.3029 | Zj | 3.444 | 3.5674 | -0.4979 | 3 | 2 | 1 | ||
| Zj-Cj | 2.444 | 1.5674 | -3.4979↑ | 0 | 0 | 0 |
Negative minimum Zj-Cj is -3.4979 and its column index is 3. So, the entering variable is x3.
Minimum ratio is 54.1905 and its row index is 1. So, the leaving
basis variable is x4.
∴ The pivot element is 0.2614.
Entering =x3, Departing =x4, Key Element =0.2614
Exercise 26:
a)
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| subject to | |||||||||||
| and x1,x2,x3≥0; |
-->Phase-1<--
| Iteration-1 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | A1 | A2 | A3 | A4 | Min Ratio XB/x2 |
| A1 | -1 | 3 | -3 | (15) | -3 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 3/15=0.2→ |
| S2 | 0 | 60 | 6 | 3 | 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 60/3=20 |
| S3 | 0 | 21 | -6 | 6 | 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21/6=3.5 |
| A2 | -1 | 21 | 9 | 5 | -1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 21/5=4.2 |
| A3 | -1 | 3 | -3 | 5 | 2 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3/5=0.6 |
| S6 | 0 | 30 | 6 | 8 | -4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 30/8=3.75 |
| S7 | 0 | 12 | 0 | 8 | -4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 12/8=1.5 |
| A4 | -1 | 12 | 3 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | --- |
| Z=-39 | Zj | -6 | -25 | -1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | -1 | -1 | -1 | -1 | ||
| Zj-Cj | -6 | -25↑ | -1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Iteration-3 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | A3 | A4 | Min Ratio XB/x3 |
| x2 | 0 | 0.6 | 0 | 1 | -0.2 | -0.06 | 0 | 0 | -0.02 | 0 | 0 | 0 | 0 | 0 | 0 | --- |
| S2 | 0 | 46.2 | 0 | 0 | 6.6 | -0.02 | 1 | 0 | 0.66 | 0 | 0 | 0 | 0 | 0 | 0 | 46.2/6.6=7 |
| S3 | 0 | 29.4 | 0 | 0 | 4.2 | 0.56 | 0 | 1 | -0.48 | 0 | 0 | 0 | 0 | 0 | 0 | 29.4/4.2=7 |
| x1 | 0 | 2 | 1 | 0 | 0 | 0.0333 | 0 | 0 | -0.1 | 0 | 0 | 0 | 0 | 0 | 0 | --- |
| A3 | -1 | 6 | 0 | 0 | (3) | 0.4 | 0 | 0 | -0.2 | -1 | 0 | 0 | 0 | 1 | 0 | 6/3=2→ |
| S6 | 0 | 13.2 | 0 | 0 | -2.4 | 0.28 | 0 | 0 | 0.76 | 0 | 1 | 0 | 0 | 0 | 0 | --- |
| S7 | 0 | 7.2 | 0 | 0 | -2.4 | 0.48 | 0 | 0 | 0.16 | 0 | 0 | 1 | 0 | 0 | 0 | --- |
| A4 | -1 | 6 | 0 | 0 | 3 | -0.1 | 0 | 0 | 0.3 | 0 | 0 | 0 | -1 | 0 | 1 | 6/3=2 |
| Z=-12 | Zj | 0 | 0 | -6 | -0.3 | 0 | 0 | -0.1 | 1 | 0 | 0 | 1 | -1 | -1 | ||
| Zj-Cj | 0 | 0 | -6↑ | -0.3 | 0 | 0 | -0.1 | 1 | 0 | 0 | 1 | 0 | 0 |
Negative minimum Zj-Cj is -1 and its column index is 8. So, the
entering variable is S5.
Minimum ratio is 0 and its row index is 8. So, the leaving basis
variable is A4.
∴ The pivot element is 1.
Entering =S5, Departing =A4, Key Element =1
R8(new)=R8(old)
R1(new)=R1(old) + 0.0667R8(new)
R2(new)=R2(old) - 2.2R8(new)
R3(new)=R3(old) - 1.4R8(new)
R4(new)=R4(old)
R5(new)=R5(old) + 0.3333R8(new)
R6(new)=R6(old) + 0.8R8(new)
R7(new)=R7(old) + 0.8R8(new)
| Iteration-5 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | Min Ratio |
| x2 | 0 | 1 | 0 | 1 | 0 | -0.0667 | 0 | 0 | 0 | 0 | 0 | 0 | -0.0667 | |
| S2 | 0 | 33 | 0 | 0 | 0 | 0.2 | 1 | 0 | 0 | 0 | 0 | 0 | 2.2 | |
| S3 | 0 | 21 | 0 | 0 | 0 | 0.7 | 0 | 1 | -0.9 | 0 | 0 | 0 | 1.4 | |
| x1 | 0 | 2 | 1 | 0 | 0 | 0.0333 | 0 | 0 | -0.1 | 0 | 0 | 0 | 0 | |
| x3 | 0 | 2 | 0 | 0 | 1 | -0.0333 | 0 | 0 | 0.1 | 0 | 0 | 0 | -0.3333 | |
| S6 | 0 | 18 | 0 | 0 | 0 | 0.2 | 0 | 0 | 1 | 0 | 1 | 0 | -0.8 | |
| S7 | 0 | 12 | 0 | 0 | 0 | 0.4 | 0 | 0 | 0.4 | 0 | 0 | 1 | -0.8 | |
| S5 | 0 | 0 | 0 | 0 | 0 | -0.5 | 0 | 0 | 0.5 | 1 | 0 | 0 | -1 | |
| Z=0 | Zj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Zj-Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Since all Zj-Cj≥0
Hence, optimal solution is arrived with value of variables as :
x1=2,x2=1,x3=2
Max Z=0
| Iteration-2 | Cj | 1 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | Min Ratio XB/S4 |
| x2 | 2 | 2 | 0 | 1 | 0 | -0.0333 | 0 | 0.0476 | -0.0429 | 0 | 0 | 0 | 0 | --- |
| S2 | 0 | 0 | 0 | 0 | 0 | -0.9 | 1 | -1.5714 | (1.4143) | 0 | 0 | 0 | 0 | 0/1.4143=0→ |
| S8 | 0 | 15 | 0 | 0 | 0 | 0.5 | 0 | 0.7143 | -0.6429 | 0 | 0 | 0 | 1 | --- |
| x1 | 1 | 2 | 1 | 0 | 0 | 0.0333 | 0 | 0 | -0.1 | 0 | 0 | 0 | 0 | --- |
| x3 | 3 | 7 | 0 | 0 | 1 | 0.1333 | 0 | 0.2381 | -0.1143 | 0 | 0 | 0 | 0 | --- |
| S6 | 0 | 30 | 0 | 0 | 0 | 0.6 | 0 | 0.5714 | 0.4857 | 0 | 1 | 0 | 0 | 30/0.4857=61.7647 |
| S7 | 0 | 24 | 0 | 0 | 0 | 0.8 | 0 | 0.5714 | -0.1143 | 0 | 0 | 1 | 0 | --- |
| S5 | 0 | 15 | 0 | 0 | 0 | 0 | 0 | 0.7143 | -0.1429 | 1 | 0 | 0 | 0 | --- |
| Z=27 | Zj | 1 | 2 | 3 | 0.3667 | 0 | 0.8095 | -0.5286 | 0 | 0 | 0 | 0 | ||
| Zj-Cj | 0 | 0 | 0 | 0.3667 | 0 | 0.8095 | -0.5286↑ | 0 | 0 | 0 | 0 |
Since all Zj-Cj≥0
Hence, optimal solution is arrived with value of variables as :
x1=2,x2=2,x3=7
Max Z=27
b)
|
|||||||||||
| subject to | |||||||||||
| and x1,x2,x3≥0; |
| Iteration-1 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | A1 | A2 | A3 | A4 | Min/Ratio XB/x2 |
| A1 | -1 | 3 | -3 | (15) | -3 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 3/15=0.2→ |
| S2 | 0 | 60 | 6 | 3 | 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 60/3=20 |
| S3 | 0 | 21 | -6 | 6 | 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21/6=3.5 |
| A2 | -1 | 21 | 9 | 5 | -1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 21/5=4.2 |
| A3 | -1 | 3 | -3 | 5 | 2 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3/5=0.6 |
| S6 | 0 | 30 | 6 | 8 | -4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30/8=3.75 |
| S7 | 0 | 12 | 0 | 8 | -4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 12/8=1.5 |
| A4 | -1 | 12 | 3 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | --- |
| S9 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | --- |
| Z=-39 | Zj | -6 | -25 | -1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | -1 | -1 | -1 | -1 | ||
| Zj-Cj | -6 | -25↑ | -1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Iteration-3 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | A3 | A4 | Min Ratio XB/x3 |
| x2 | 0 | 0.6 | 0 | 1 | -0.2 | -0.06 | 0 | 0 | -0.02 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | --- |
| S2 | 0 | 46.2 | 0 | 0 | 6.6 | -0.02 | 1 | 0 | 0.66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 46.2/6.6=7 |
| S3 | 0 | 29.4 | 0 | 0 | 4.2 | 0.56 | 0 | 1 | -0.48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 29.4/4.2=7 |
| x1 | 0 | 2 | 1 | 0 | 0 | 0.0333 | 0 | 0 | -0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | --- |
| A3 | -1 | 6 | 0 | 0 | 3 | 0.4 | 0 | 0 | -0.2 | -1 | 0 | 0 | 0 | 0 | 1 | 0 | 6/3=2 |
| S6 | 0 | 13.2 | 0 | 0 | -2.4 | 0.28 | 0 | 0 | 0.76 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | --- |
| S7 | 0 | 7.2 | 0 | 0 | -2.4 | 0.48 | 0 | 0 | 0.16 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | --- |
| A4 | -1 | 6 | 0 | 0 | 3 | -0.1 | 0 | 0 | 0.3 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 6/3=2 |
| S9 | 0 | 1 | 0 | 0 | (2) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1/2=0.5→ |
| Z=-12 | Zj | 0 | 0 | -6 | -0.3 | 0 | 0 | -0.1 | 1 | 0 | 0 | 1 | 0 | -1 | -1 | ||
| Zj-Cj | 0 | 0 | -6↑ | -0.3 | 0 | 0 | -0.1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Negative minimum Zj-Cj is -6 and its column index is 3. So, the
entering variable is x3.
Minimum ratio is 0.5 and its row index is 9. So, the leaving basis
variable is S9.
∴ The pivot element is 2.
Entering =x3, Departing =S9, Key Element =2
R9(new)=R9(old)÷2
R1(new)=R1(old) + 0.2R9(new)
R2(new)=R2(old) - 6.6R9(new)
R3(new)=R3(old) - 4.2R9(new)
R4(new)=R4(old)
R5(new)=R5(old) - 3R9(new)
R6(new)=R6(old) + 2.4R9(new)
R7(new)=R7(old) + 2.4R9(new)
R8(new)=R8(old) - 3R9(new)
Negative minimum Zj-Cj is -0.3 and its column index is 4. So, the
entering variable is S1.
Minimum ratio is 11.25 and its row index is 5. So, the leaving basis
variable is A3.
∴ The pivot element is 0.4.
Entering =S1, Departing =A3, Key Element =0.4
R5(new)=R5(old)÷0.4
R1(new)=R1(old) + 0.06R5(new)
R2(new)=R2(old) + 0.02R5(new)
R3(new)=R3(old) - 0.56R5(new)
R4(new)=R4(old) - 0.0333R5(new)
R6(new)=R6(old) - 0.28R5(new)
R7(new)=R7(old) - 0.48R5(new)
R8(new)=R8(old) + 0.1R5(new)
R9(new)=R9(old)
| Iteration-5 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | A4 | Min Ratio XB/S4 |
| x2 | 0 | 1.375 | 0 | 1 | 0 | 0 | 0 | 0 | -0.05 | -0.15 | 0 | 0 | 0 | -0.125 | 0 | --- |
| S2 | 0 | 43.125 | 0 | 0 | 0 | 0 | 1 | 0 | 0.65 | -0.05 | 0 | 0 | 0 | -3.375 | 0 | 43.125/0.65=66.3462 |
| S3 | 0 | 21 | 0 | 0 | 0 | 0 | 0 | 1 | -0.2 | 1.4 | 0 | 0 | 0 | 0 | 0 | --- |
| x1 | 0 | 1.625 | 1 | 0 | 0 | 0 | 0 | 0 | -0.0833 | 0.0833 | 0 | 0 | 0 | 0.125 | 0 | --- |
| S1 | 0 | 11.25 | 0 | 0 | 0 | 1 | 0 | 0 | -0.5 | -2.5 | 0 | 0 | 0 | -3.75 | 0 | --- |
| S6 | 0 | 11.25 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9 | 0.7 | 1 | 0 | 0 | 2.25 | 0 | 11.25/0.9=12.5 |
| S7 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | (0.4) | 1.2 | 0 | 1 | 0 | 3 | 0 | 3/0.4=7.5→ |
| A4 | -1 | 5.625 | 0 | 0 | 0 | 0 | 0 | 0 | 0.25 | -0.25 | 0 | 0 | -1 | -1.875 | 1 | 5.625/0.25=22.5 |
| x3 | 0 | 0.5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0 | --- |
| Z=-5.625 | Zj | 0 | 0 | 0 | 0 | 0 | 0 | -0.25 | 0.25 | 0 | 0 | 1 | 1.875 | -1 | ||
| Zj-Cj | 0 | 0 | 0 | 0 | 0 | 0 | -0.25↑ | 0.25 | 0 | 0 | 1 | 1.875 | 0 |
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| subject to | |||||||||||
| and x1,x2,x3≥0; |
The problem is converted to canonical form by adding slack, surplus
and artificial variables as appropiate
1. As the constraint-1 is of type '≥' we should subtract surplus
variable S1 and add artificial variable A1
2. As the constraint-2 is of type '≤' we should add slack
variable S2
3. As the constraint-3 is of type '≤' we should add slack
variable S3
4. As the constraint-4 is of type '≥' we should subtract surplus
variable S4 and add artificial variable A2
After introducing slack, surplus, artificial variables
| Iteration-1 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | A1 | A2 | Min/Ratio XB/x2 |
| A1 | -1 | 3 | -3 | (15) | -3 | -1 | 0 | 0 | 0 | 1 | 0 | 3/15=0.2→ |
| S2 | 0 | 60 | 6 | 3 | 6 | 0 | 1 | 0 | 0 | 0 | 0 | 60/3=20 |
| S3 | 0 | 21 | -6 | 6 | 3 | 0 | 0 | 1 | 0 | 0 | 0 | 21/6=3.5 |
| A2 | -1 | 21 | 9 | 5 | -1 | 0 | 0 | 0 | -1 | 0 | 1 | 21/5=4.2 |
| Z=-24 | Zj | -6 | -20 | 4 | 1 | 0 | 0 | 1 | -1 | -1 | ||
| Zj-Cj | -6 | -20↑ | 4 | 1 | 0 | 0 | 1 | 0 | 0 |
Negative minimum Zj-Cj is -20 and its column index is 2. So, the
entering variable is x2.
Minimum ratio is 0.2 and its row index is 1. So, the leaving basis
variable is A1.
∴ The pivot element is 15.
Entering =x2, Departing =A1, Key Element =15
R1(new)=R1(old)÷15
R2(new)=R2(old) - 3R1(new)
R3(new)=R3(old) - 6R1(new)
R4(new)=R4(old) - 5R1(new)
| Iteration-3 | Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | Min Ratio |
| x2 | 0 | 0.6 | 0 | 1 | -0.2 | -0.06 | 0 | 0 | -0.02 | |
| S2 | 0 | 46.2 | 0 | 0 | 6.6 | -0.02 | 1 | 0 | 0.66 | |
| S3 | 0 | 29.4 | 0 | 0 | 4.2 | 0.56 | 0 | 1 | -0.48 | |
| x1 | 0 | 2 | 1 | 0 | 0 | 0.0333 | 0 | 0 | -0.1 | |
| Z=0 | Zj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Zj-Cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Negative minimum Zj-Cj is -3.4 and its column index is 3. So, the
entering variable is x3.
Minimum ratio is 7 and its row index is 3. So, the leaving basis
variable is S3.
∴ The pivot element is 4.2.
Entering =x3, Departing =S3, Key Element =4.2
R3(new)=R3(old)÷4.2
R1(new)=R1(old) + 0.2R3(new)
R2(new)=R2(old) - 6.6R3(new)
R4(new)=R4(old)
| Iteration-2 | Cj | 1 | 2 | 3 | 0 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| B | CB | XB | x1 | x2 | x3 | S1 | S2 | S3 | S4 | Min Ratio XB/S4 |
| x2 | 2 | 2 | 0 | 1 | 0 | -0.0333 | 0 | 0.0476 | -0.0429 | --- |
| S2 | 0 | 0 | 0 | 0 | 0 | -0.9 | 1 | -1.5714 | (1.4143) | 0/1.4143=0→ |
| x3 | 3 | 7 | 0 | 0 | 1 | 0.1333 | 0 | 0.2381 | -0.1143 | --- |
| x1 | 1 | 2 | 1 | 0 | 0 | 0.0333 | 0 | 0 | -0.1 | --- |
| Z=27 | Zj | 1 | 2 | 3 | 0.3667 | 0 | 0.8095 | -0.5286 | ||
| Zj-Cj | 0 | 0 | 0 | 0.3667 | 0 | 0.8095 | -0.5286↑ |
Negative minimum Zj-Cj is -0.5286 and its column index is 7. So, the
entering variable is S4.
Minimum ratio is 0 and its row index is 2. So, the leaving basis
variable is S2.
∴ The pivot element is 1.4143.
Entering =S4, Departing =S2, Key Element =1.4143
R2(new)=R2(old)÷1.4143
R1(new)=R1(old) + 0.0429R2(new)
R3(new)=R3(old) + 0.1143R2(new)
R4(new)=R4(old) + 0.1R2(new)
-6X1 + 6X2 + 3X3 ≤ 21,
9X1 + 5X2 - X3 ≥ 21,
X1, X2, X3>0
Exercise 28: LP Transportation problem
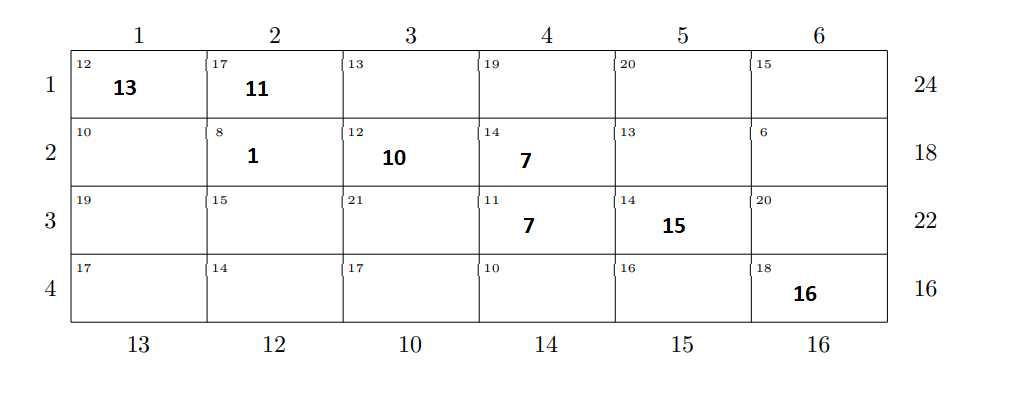
17X41+14X42+17X43+10X44+16X45+18X46
Subject to
X11+X21+X31+X41=13
X12+X22+X32+X42=12
Number of basic variables = m + n – 1 = 4+ 6 – 1 = 9.
The total transportation cost is calculated by multiplying each xij in an occupied cell with the corresponding cij and adding as follows:
Exercise 29: ManualSimplex LP implementation
Origin:
x12+x14-z=0
x23+x43-x36=0
Destination:
x25<=3
x23<=5
Send 2 unit from 1 to 2
Send 2 unit from 2 to 5
The maximum flow is 3 unit.
Chapter 12:
Exercise 30—W = 15 and
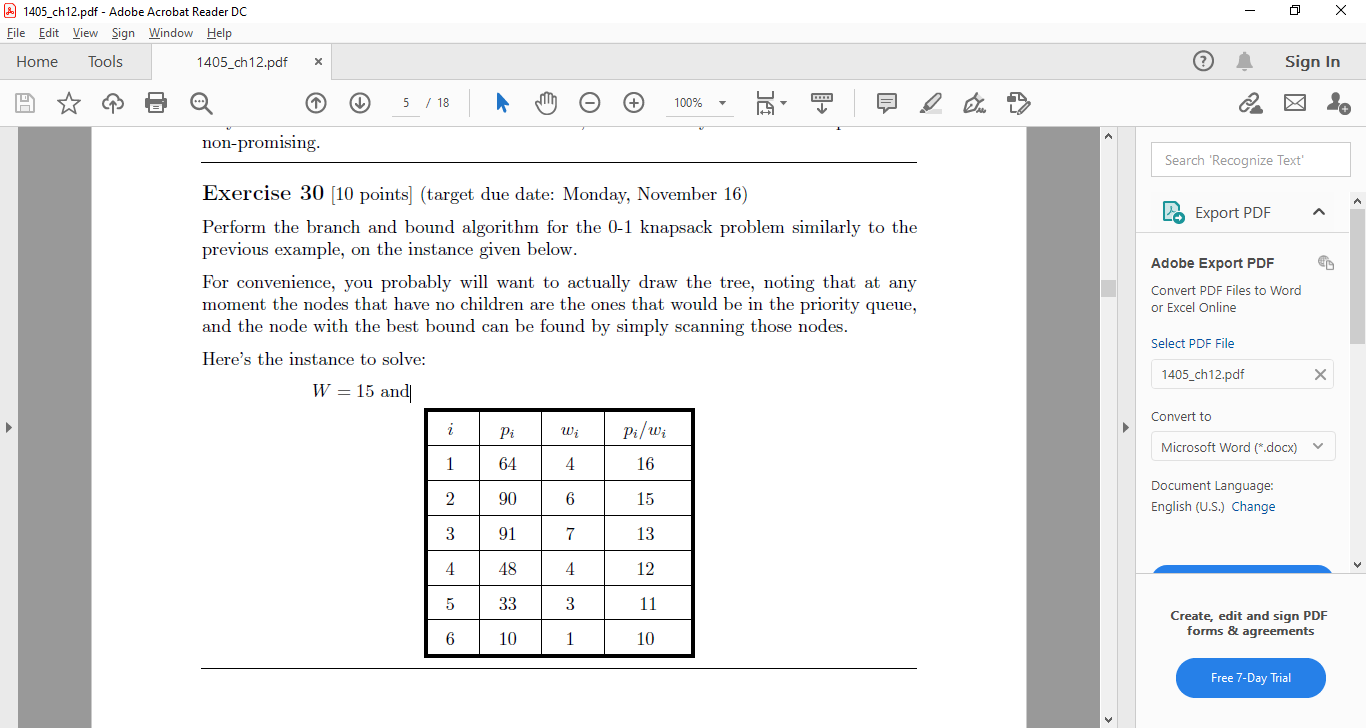
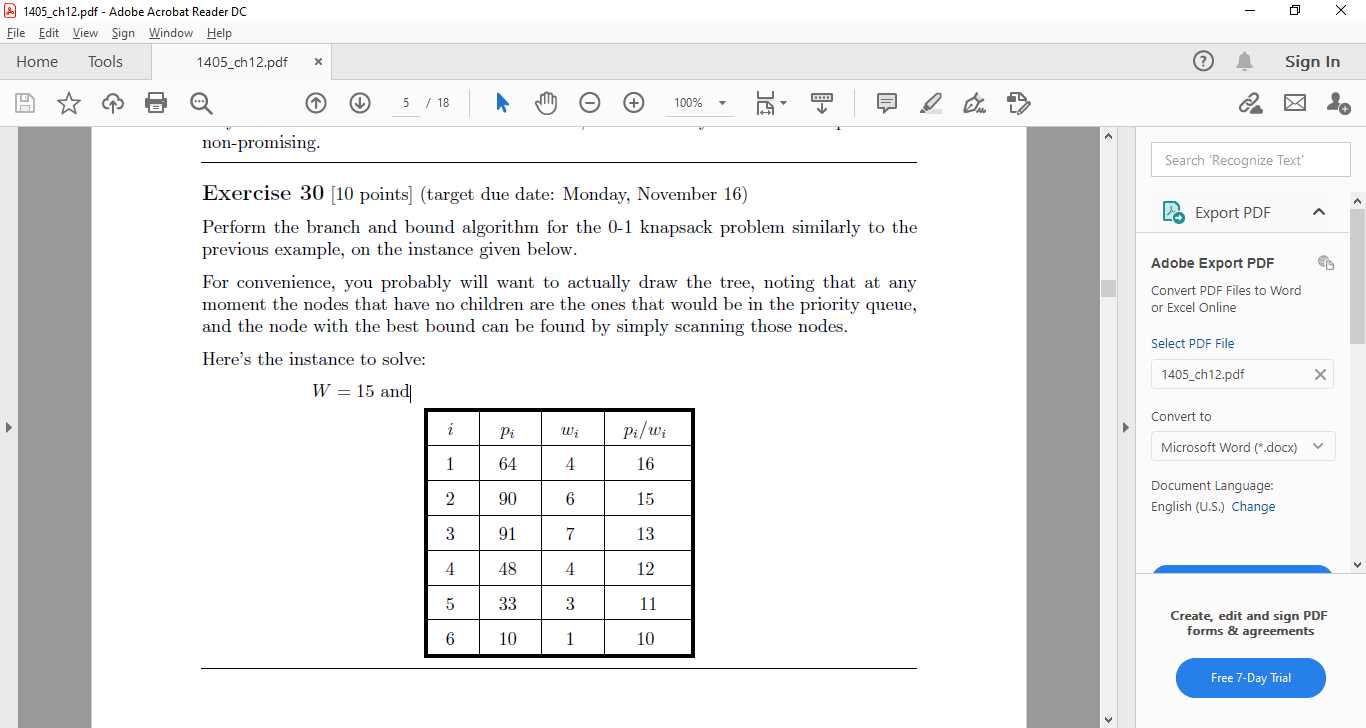
Initialize maxProfit = 0;
Dequeue the Node u and and enqueue next level node I,e. node 1.
Profit of node 1 = 64, update maxProfit if profit of node is more.
So, Enqueue Node 2 to Queue.
Again, Repeat till Queue is not empty.
Print the MaxProfit = 154.
Item 1 fits give profit of 64 and weight of 4.
64 + 90 + 65 = 219.
| {} | |
|---|---|
| 0 | 0 |
| 219 | |
90 + 91+ 24 = 205, for remove node 1 and enqueue 2
| {1} | |
|---|---|
| 64 | 4 |
| 219 | |
| { |
|
|---|---|
| 0 | 0 |
| 205 | |
| {1, |
|
|---|---|
| 64 | 4 |
| 219 | |
| { |
|
|---|---|
| 0 | 0 |
| 154 | |
Exercise 31: Java code to implement the solution
Output:

Q32)
Bad1 traversal is better score than Bad2. As we can see the output screen for both bad1 and bad2. Bad1 is far better than bad2
Exercise 33
56.29+8.54+31.40+26.93+22.14+53.85+25.00+16.03+13.60+14.00+50.70=318.48
