Identify apply snells law the water ice and ice air interfaces
| EXECUTE: |
|
14.0 cm | , so | φ = | 50.6° . θ | = | 90° | − | φ = | 39.4 | °and | θ | = | θ | = |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11.5 cm | r | r | a |
Figure 33.2
33-1
| 33.3. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n | = | c | so v | = | c | = | 2.998 10 m/s 8 | = |
|
||||||||||||||||||||||||||||||||||||||||||||
| v | n | 1.47 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | λ = | λ 0 | = | 650 nm | = | |||||||||||||||||||||||||||||||||||||||||||||||||
| 33.4. | n | 1.47 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| v | = | f λ | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| c | = | f λ 0 | . In glass, | λ = | λ 0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
| n | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c = | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| λ 0 | = | c | = | = | ||||||||||||||||||||||||||||||||||||||||||||||||||
| f | 5.80 10 Hz 14 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | λ = | λ 0 | = | 517 nm | = |
|
||||||||||||||||||||||||||||||||||||||||||||||||
| 33.5. | n | 1.52 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| IDENTIFY: | n | = | c | . | λ = | λ 0 | , where | |||||||||||||||||||||||||||||||||||||||||||||||
| v | n | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| c = | 3.00 10 m/s 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| n | = | c | = | 3.00 10 m/s 8 | = | 1.54. | ||||||||||||||||||||||||||||||||||||||||||||||||
| 33.6. | v | 1.94 10 m/s 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | λ 0 | = | n λ = |
|
−7 | m) | = | 5.47 10× | −7 |
|
||||||||||||||||||||||||||||||||||||||||||||
| IDENTIFY: | λ = | λ 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| n | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n water | = | 1.333 | and | n benzene | = | 1.501 | ||||||||||||||||||||||||||||||||||||||||||||||||
|
λ water | n water | = | λ benzene | n benzene | = | λ 0 | . | λ benzene | = | λ water |
|
n water | ⎞ | = | (438 nm) | ⎛ | 1.333 | ⎞ | = | 389 nm | |||||||||||||||||||||||||||||||||
| 33.7. | n benzene | ⎠ | ⎜⎝ | 1.501 | ⎟⎠ | |||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | λ 0 | = | λ water | n water | = | (438 nm)(1.333) | = | |||||||||||||||||||||||||||||||||||||||||||||||
| EVALUATE: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| θ r | and θ The angles in these equations are measured with b | |||||||||||||||||||||||||||||||||||||||||||||||||||||
respect to the normal, not the surface.
(a) SET UP: The incident, reflected and refracted rays are shown in Figure 33.7.
| angle of 90.0° −θ r | = |
|---|
Figure 33.7
EVALUATE: The light is bent toward the normal when the light enters the material of larger refractive index.
| 33.9. | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EXECUTE: | n a | sin θ a | = | n b |
|
|||||||||||||||||
| n b | = | n a | ⎛ | sin θ a |
|
= | 1.00 | ⎛ | sin62.7° | ⎞ | = | |||||||||||
| ⎜⎝ | sin θ b | ⎜⎝ | sin48.1° | ⎟⎠ | ||||||||||||||||||
| n | = | c | so | = | c | = | (3.00 10 m/s)/1.194 8 | = | ||||||||||||||
| v | n | |||||||||||||||||||||
SET UP: Let the light initially be in the material with refractive index
| index | bn . In part (a) let the middle slab have refractive index |
|
|---|
gives n a sin θ a = n b sin θ b .
EVALUATE: The final direction of travel depends on the angle of incidence in the first slab and the refractive
boundary is the same on both sides of the boundary, so the frequency does not change. The wavelength and speed
n
⎟ |
|||||||
|---|---|---|---|---|---|---|---|
| v′ = | c | = | nv | =⎛ | n | ⎞ | |
| n′ | n′ | n′ | ⎟⎠ | ||||
without referring them to the values in vacuum (or air).
the two angles labeled φ′are equal because of the law of reflection. The two angles labeled θare equal because the
lines forming one angle are perpendicular to the lines forming the other angle.
| 33.15. | Figure 33.14 | 62.0 | °. | bn = | 1.58 |
|
|||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
n a | sin θ a | = | n b | sin θ b | ||||||||||||||||||||||||
| an = | 1.70 | , | θ = a | ||||||||||||||||||||||||||
| EXECUTE: | = | ⎛ | n a | ⎞ | sin θ a | = | ⎛ | 1.70 | ⎞ | sin62.0° | = | 0.950 | and | θ = b | |||||||||||||||
| b | ⎜⎝ | n b | ⎟⎠ | ⎜⎝ | 1.58 | ⎟⎠ | |||||||||||||||||||||||
EVALUATE: The ray refracts into a material of smaller n, so it is bent away from the normal.
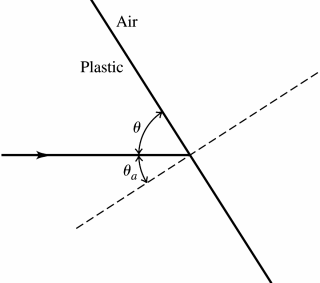
Figure 33.17
| 33.18. | IDENTIFY: Since the refractive index of the glass is greater than that of air or water, total internal reflection will |
|---|
(b) Using the same procedure as in part (a), we have 1.53 sin θc = 1.333 sin 90° and θc = 60.6°.
EVALUATE: Since the refractive index of water is closer to the refractive index of glass than the refractive index of air is, the critical angle for glass-to-water is greater than for glass-to-air.
| 33.20. | ||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| → | air |
|
||||||||||||||||||||||||||||||||||||
| SET UP: Figure 33.20 shows a ray incident at the critical angle and therefore at the edge of the ring of light. The | ||||||||||||||||||||||||||||||||||||||
|
d = | 10.0 m | ||||||||||||||||||||||||||||||||||||
| r | = | d | tan θ crit | . θ crit | is calculated from | n a | sin θ a | = | n b | sin θ b | with | an = | 1.333 | , θ a | = | θ crit | ||||||||||||||||||||||
| bn = | 1.00 | and θ = b | 90 | °. | sin θ crit | = |
|
= | 48.6°. | r = | (10.0 m)tan48.6° | = | 11.3 m |
|
||||||||||||||||||||||||
| A | = | π r | 2 | = | π (11.3 m) | 2 | = | 401 m | 2 | |||||||||||||||||||||||||||||
|
n glass | > | n water, |
|
|---|
|
α + | θ crit | = | 90°. | = | n b | sin θ b | gives | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
θ a | = | θ crit, | an = | bn = | 1.00 | and | θ = b | 90 .° | n a | sin θ a | |||||||||||||||||||||||||||||
| sin θ crit | = | θ crit | = | 41.1°. | α = | 90° | − | θ crit | = | |||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
→ | water | and | bn = | 1.333 | . | n a | sin θ a | = | n b | sin θ b | gives | sin θ crit | = | ||||||||||||||||||||||||||
| 1.52 | ||||||||||||||||||||||||||||||||||||||||
| and θ crit | = | 61.3°. α = | 90° | −θ crit | = | |||||||||||||||||||||||||||||||||||
Figure 33.22
| 33.24. | n a | sin θ a | = | n | sin θ | . | v | = | c | ||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b | b | n | |||||||||||||||||||||||||||||||||||||||||
| SET UP: | a = | air | , | b = | glass | ||||||||||||||||||||||||||||||||||||||
|
n b | = | n a | sin θ a | = | (1.00)sin57.0 | ° | = | 1.36 | . violet: | n = | (1.00)sin57.0° | = | 1.40 |
|
||||||||||||||||||||||||||||
| sin θ b | b | sin36.7° | |||||||||||||||||||||||||||||||||||||||||
| (b) red: | v | = | c | = | 3.00 10 m/s 8 | = | 2.21 10 m/s | ; violet: | v | = | c | = | 3.00 10 m/s 8 | = | 2.14 10 m/s | ||||||||||||||||||||||||||||
| n | 1.36 | n | 1.40 | ||||||||||||||||||||||||||||||||||||||||
33.25. IDENTIFY: When unpolarized light passes through a polarizer the intensity is reduced by a factor of 1 2and the
transmitted light is polarized along the axis of the polarizer. When polarized light of intensity I max is incident on a
the intensity is ( I 0 /2)(cos60 ) 2 = 0.125 I 0 , and the light is polarized along the axis of the second polarizer. At
point C the intensity is (0.125 )(cos30 ) 0 2 = 0.0938 I 0 .
Figure 33.26
33.27. IDENTIFYand SET UP: Reflected beam completely linearly polarized implies that the angle of incidence equals
| tan θ p | = | n b | gives n glass | = | tan θ | = | (1.00)tan54.5° = |
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n a | air | p | ||||||||||||||||||
| (b) | n a | sin θ a | = | n b |
|
= | ||||||||||||||
| sin θ b | = | n a | sin θ a | = | (1.00)sin54.5° | = | 0.5815 and θ b | |||||||||||||
| 1.40 | ||||||||||||||||||||
Note: φ = 180.0° −θ r−θ b and θ r = θ a . Thus
φ = 180.0° −54.5° −35.5° = 90.0 ;° the
|
I = | I | 0 | and the light is polarized along the vertical direction. After the second | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | |||||||||||||||||||||||||
| filter we want | I = | I 0 , |
so | I | 0 | I 2 0 (cos )⎞⎟⎠ | 2 | . cos φ = | and | φ = | |||||||||||||||
| 10 |
|
||||||||||||||||||||||||
|
0I of the incident light. For the second filter | I | 0 | = | I | 2 | |||||||||||||||||||
| 10 | |||||||||||||||||||||||||
| cos φ = | 1/10 | and | φ = | ||||||||||||||||||||||
EVALUATE: When the incident light is polarized along the axis of the first filter, φ must be larger to achieve the
same overall reduction in intensity than when the incident light is unpolarized.
|
||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 33.30. |
|
|||||||||||||||||||
| tan θ = p | n b | |||||||||||||||||||
| n a | ||||||||||||||||||||
| bn = | 1.66 | . | ||||||||||||||||||
| an = | 1.00 | . | tan θ = p | 1.66 | and | θ = |
|
|||||||||||||
| 1.00 | p | |||||||||||||||||||
| (b) | n = | 1.333 | . | tan θ = p | 1.66 | and | θ = p |
|
||||||||||||
| a | 1.333 | |||||||||||||||||||
SET UP: For the second filter, φ = 62.0°−25.0°= 37.0° .
EXECUTE: After the first filter the intensity is
1
33.32. IDENTIFY: After passing through the first filter the light is linearly polarized along the filter axis. After the
second filter, I = I max(cos ) 2 , where φ is the angle between the axes of the two filters.
EVALUATE: As φ increases toward 90° the axes of the two filters are closer to being perpendicular to each other
and the transmitted intensity decreases.
Figure 33.33a
| I | = | 1 | I | 0 | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | ||||||||||||||||||||||||||||||||
| I | 2 | = | I 1 | cos | 2 | φ = | ( | 1 | I | )(cos45.0 ) | 2 | = | 0.250 | I | 0 | and the light is linearly polarized | |||||||||||||||||
| 2 | 0 | ||||||||||||||||||||||||||||||||
| I | 3 | = | I | 2 | cos | 2 | φ = | 0.250 | I | 0 | (cos45.0 )° | 2 |
|
||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
light is linearly polarized along the axis of the first polarizer.
Figure 33.33b
| = | I | cos | 2 | φ = | ( | 1 | )(cos90.0 | 2 | = | 0. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 1 | 2 | 0 |
0I . Then repeat the calculation with only the first and third polarizers.
|
||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | = | ( | I | )(cos23.0 ) (cos[62.0° | − | 23.0 ]) | 2 | = | 0.256 | I | . | I = 0 | I | = | 75.0 W/cm 2 | = | 293 W/cm | 2 |
|
|||||||||||||
| 2 | 0 | 0 | 0.256 | 0.256 | ||||||||||||||||||||||||||||
| I | = | 2( | I | 0 | )(cos62.0 ) | 2 | = | 0.110 | I | 0 | = | (0.110)(293 W/cm ) 2 | = | 32.2 W/cm | 2 | |||||||||||||||||
SET UP: The intensity of the scattered light is proportional to 1/λ4, we can write it as I = (constant)/λ4.
EXECUTE:(a) Since I is proportional to 1/λ4, we have I = (constant)/λ4. Taking the ratio of the intensity of the
EVALUATE: In the scattered light, the intensity of the short-wavelength violet light is about 7 times as great as that of the red light, so this scattered light will have a blue-violet color.
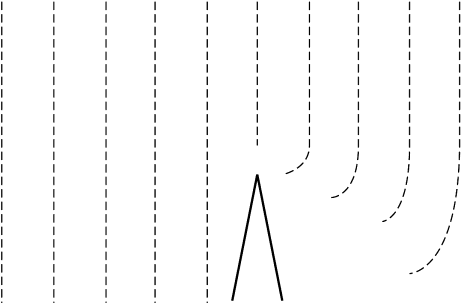
Figure 33.36
SET UP: The definition of the index of refraction is n = c/v, where v is the speed of light in the jelly.
EXECUTE: First get the length L of the tube using air. In the air, we have L = ct = (3.00 × 108 m/s)(8.72 ns) = 2.616 m.
| 33.40. | n | = | c | and λ = | λ 0 | . | |
|---|---|---|---|---|---|---|---|
| IDENTIFY: Use the change in transit time to find the speed v of light in the slab, and then apply | |||||||
| v | n |
SET UP: The ray is sketched in Figure 33.41.
EXECUTE: For glass→air at point A, Snell's law gives (1.38)sin θ crit = (1.00)sin90°and θ crit = 46.4°.
Figure 33.41
33.42. IDENTIFY: As the light crosses the glass-air interface along AB, it is refracted and obeys Snell’s law.
EVALUATE: The lower ray is deflected more than the upper ray because that wavelength has a slightly greater
index of refraction than the upper ray.
| 33.43. |
|---|
EXECUTE: In the circularly polarized light the two perpendicular polarization components are 90° out of phase.
The quarter-wave plate shifts the relative phase by 90° and then the two components are either in phase or
wavelength in the material.
|
d | glass | = | 0.00250 m | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | air | = | 0.0180 m | − | 0.00250 m | = | 0.0155 m | |||||
EVALUATE: Without the glass plate the number of wavelengths between the source and screen is
|
= | 3.33 10× | 4 | ||
|---|---|---|---|---|---|
| 33.45. | |||||
edge of the halo.
SET UP: The ray incident at the critical angle is sketched in Figure 33.45.
|
|
|---|---|
| 33.47. | IDENTIFY: Use Snell’s law to determine the effect of the liquid on the direction of travel of the light as it enters |
the liquid.
After the liquid is poured in, θ is the same and the refracted ray passes through the center of the bottom of the a
glass, as shown in Figure 33.47b.
| tan θ = b | 4.0 cm | = | |||
|---|---|---|---|---|---|
| 16.0 cm | |||||
| θ = b | |||||
bn the refractive index of the liquid:
| n | = | n a | sin θ a | = | (1.00)(sin26.57 ) | = | |
|---|---|---|---|---|---|---|---|
| b | sin θ b | sin14.04° | |||||
EXECUTE: Apply Snell's law to the air→liquid refraction. (1.00)sin(42.5 ) = (1.63)sin θ b and θ = b 24.5°.
θ b = φ and φ = θ′a , so θ a′ = θ b = 24.5°. Snell's law applied to the liquid→air refraction gives
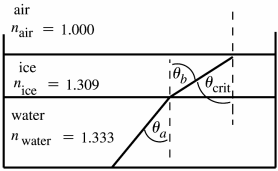
Figure 33.49
| 33.50. | → | water | ||
|---|---|---|---|---|
SET UP: The path of the ray is sketched in Figure 33.50. The ray enters the prism at normal incidence so is not
|
||||
|---|---|---|---|---|
|
||||
| n glass | > | n water | ||
SET UP: The paths of the two rays are sketched in Figure 33.51.
| EXECUTE: | n a | sin θ a | = | n b | 25.0 | ° − | 45.45 | ° = | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n glassin25.0° = |
|
19.55 .° The angle between the two rays is 2 δ = | ||||||||||||||||||
| sin θ = b | n glass |
|
||||||||||||||||||
| sin θ = b | 1.66sin25.0° = | 0.7015 | ||||||||||||||||||
| θ = b | ||||||||||||||||||||
| β | = | 90.0° −θ b | = | |||||||||||||||||
| Then | δ | = | 90.0° − | A | − | β | = | 90.0 | ° − | |||||||||||
EXECUTE:(a) In the water, θ = S R= (1.09 m)/(1.10 m) = 0.991 rad = 56.77°. This is the critical angle. So, using the refractive index for water from Table 33.1, we get n = (1.333) sin 56.77° = 1.12
(b) (i) The laser beam stays in the water all the time, so
| t = 2R/v = 2R/ | ⎛ | c | ⎞ | = | Dn water |
|
|---|---|---|---|---|---|---|
| ⎜⎝ | n water | ⎟⎠ | c |
The total time is 4.09 ns + (9.78 ns)/2 = 8.98 ns
EVALUATE: The gas must be under considerable pressure to have a refractive index as high as 1.12.
| 33.54. |
|
||
|---|---|---|---|
| applies at that glass-water surface, and the index of refraction is defined as n = | c | ||
| v | |||
SET UP: The path of a ray from the sun is sketched in Figure 33.55.
| n a | sin θ a | = | n b |
|
|---|
(a = vacuum of space, refractive, index 1.0; b = atmosphere, refractive index n)
EVALUATE: The calculated δ is about the same as the angular radius of the sun.
| d | = | ( | x | 2 | + | y 2 1/2 ) | + | (( l | − | x | ) | 2 | + | y | 2 1/2 ) | . | Then the time taken to travel that distance is | t | = | d | = | ( | x | 2 | + | y 1 2 1/2 ) | + | (( l | − | x | ) | 2 | + | y | 2 2 1/2 ) | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c | c |
(b) Taking the derivative with respect to x of the time and setting it to zero yields
|
|
|---|---|
| 33.57. | IDENTIFYand SET UP: Find the distance that the ray travels in each medium. The travel time in each medium is |
SET UP: Refer to the angles and distances defined in the figure that accompanies the problem.
|
||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | sin θ a | = | n′ | sin θ b′ | = | n′ | sin θ b | = | n | sin θ a′ | ⇒ | sin θ a | = | sin θ a′ | ⇒ | θ a | = | θ a′ | ||||||||||||||||||||||||
| θ n′ = | θ n | |||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
| d | = | L | sin( θ a |
|
) and | L | = | t | ⇒ | d | = | t | sin( θ a | −θ b′ | ) | |||||||||||||||||||||||||||
| cos θ b′ | cos θ b′ | |||||||||||||||||||||||||||||||||||||||||
| (d) | θ b′ = | arcsin | ⎛ | n | sin θ a | = | arcsin | ⎛ | sin66.0° | ⎞ | = | 30.5° | and | d | = | (2.40 cm)sin(66.0 | ° − | 30.5 ) | = | |||||||||||||||||||||||
| ⎜⎝ | ⎜⎝ | 1.80 | ⎟⎠ | cos30.5° | ||||||||||||||||||||||||||||||||||||||
EVALUATE: The lateral displacement in part (d) is large, of the same order as the thickness of the plate.
| n 1 | sin θ | = | n 2 | sin α |
|---|
surface of the film at an angle of incidence α . Snell’s law applied to the refraction as ray B leaves the film gives
they emerge from the film.
| 33.60. |
|
n = v | 1.66 |
|
|||
|---|---|---|---|---|---|---|---|
| n = r | 1.61 | for red light and | |||||
|
n a | sin θ a | = | n | sin θ b | gives sin θ = a | n b |
|
. But | θ a | = | A | + | α | , so | sin | ⎛ | A | + | α⎞ | = | sin | A | + | 2 α | = | n | sin | A | . | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b | 2 | ⎜⎝ | 2 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||
| δ | and sin | A | + | δ | = | n | sin | A | ||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
δ | = | 2arcsin | ⎛ | n |
|
⎞ | − | A | . | δ | = | 60.0° | − | 60.0° = | 38.9 .° | ||||||||||||||||||||||||||||||||||||
| ⎜⎝ | ⎟⎠ | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||
(c) If two colors have different indices of refraction for the glass, then the deflection angles for them will differ:
| 33.62. |
|
|---|
is 90.00° – 58.15° = 31.85°. Applying Snell’s law at the water surface gives
| EXECUTE: The total transmitted intensity is | I | = | 1 | I | 0 | + | I | p | cos ( 2 φ− | θ ). | This is maximum when θ | = | φ and from the | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| φ−θ | = | 90° and from the data this occurs for | φ = | 125 .° Thus, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| θ | = | φ− | 90° = | 125° − | 90° = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) IDENTIFYand SET UP: | I | = | 1 | I | 0 | + | I | p | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I | 0 | and . p | Use data where the |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ( φ = | 30 )° and where it is small ( φ = | 130 )° to have the greatest sensitivity to both | I | 0 | and I | p |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| EXECUTE: | φ = | 30 gives 24.8 W/m | 2 | = | 1 | I | + | I | p | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | = | 0.500 | I | 0 | + | 0.9924 | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| φ = | 130 gives 5.2 W/m | 2 | = | 1 | I | 0 | + | I | p |
|
35 ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 | = | 0.500 | I | 0 + | 0.0076 | I | p | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19.6 W/m | 2 | = | 0.9848 | I | p | and I | p | = | 19.9 W/m . 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I = 0 | 2(5.2 W/m | 2 | − | 0.0076(19.9 W/m )) 2 | = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I | 0 | , I | p | and θ we can verify that | I | = | 1 | I | 0 | + | I | p | cos ( 2 φ−θ ) | describes that data in the | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33.64. | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33.65. | IDENTIFY: Follow the steps specified in the problem. | β ) | = | sin α cos | β− | cos α sin | β |
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SET UP: |
|
β ) | = | sin α sin | β + | cos α cos | β | . sin( α− | ||||||||
The Nature and Propagation of Light 33-19
(b) Multiplying Eq. (1) by cos β and Eq. (2) by cosα yields:
| (1): | x | cos | β | = | sin ω | cos α cos | β− | cos ω | sin α cos | β | and (2): | y | cos α = | sin ω | cos | β cos α− | cos ω | sin | β cos α | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | a | |||||||||||||||||||||||||||
| x | cos | β− | y | cos α | = − | cos ω | (sin α cos | β− | sin | |||||||||||||||||||
| a | ||||||||||||||||||||||||||||
(d) Expanding the left-hand side, we have:
| x | 2 | (sin | 2 | β + | cos | 2 | β ) | + | y | 2 | (sin | 2 | α + | cos | 2 | α ) | − | 2 | xy | (sin α sin | β + | cos α cos | |||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| = | x | 2 | + | y | 2 | − | 2 | xy | (sin α sin | β + | cos α cos | β ) | = | x | 2 | + | y | 2 | − | 2 | xy | cos( α− | |||||||||||||||||||||||||||||||||||||||||||||||||||
| The right-hand side can be rewritten: | a | 2 | (sin α cos | β− | sin | β cos ) | 2 | = | a | 2 | sin ( 2 α− | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x | 2 | + | y | 2 | − | 2 | xy | cos( α− | β ) | = | a | 2 | sin ( 2 α− | β ). Or, | x | 2 | + | y | 2 | − | 2 | xy | cos δ | = | a | 2 | sin | 2 | δ , where | δ | = | α− | |||||||||||||||||||||||||||||||||||||||||
|
δ = | 0: | x | 2 | + | y | 2 | − | 2 | xy | = | ( | x | − | y | ) | 2 | = | 0 | ⇒ | x | = | y | , which is a straight diagonal line | |||||||||||||||||||||||||||||||||||||||||||||||||
| δ = | π | : | x | 2 | + | y | 2 | − | 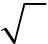 2 xy 2 xy |
= | a | 2 | , which is an ellipse | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33.66. | 4 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| δ = | π 2x |
2 | + | y | 2 | = | a | 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
larger for red than for violet, so red in the rainbow is higher above the horizon. 33.67. IDENTIFY: Follow similar steps to Challenge Problem 33.66.
SET UP: Refer to Figure 33.20e in the textbook.
| Δ = | θ a A | −θ b A | + | π− | 2 θ b A | + | π− | 2 θ b A | + θ a A | −θ b A | = | 2 θ a A | − | 6 θ b A | + | 2 , |
|---|





| 233.2° and | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (b) | d | Δ | = | 0 | = | 2 | − | 6 | d | arcsin | 1 | sin θ a A |
|
|
⇒ | 0 | = | 2 | − | 1 | . | ⎛ | cos θ 2 | . | |||||||||||||||||||||||||||||||||||||||||||||||
| d θ a A | d θ a A | n | − | sin θ 2 | ⎜⎝ | n | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| n | 2 | ⎛ | 1 | − | sin | 2 | θ 2 | = | ( | n | 2 | − + | cos | 2 | θ 2 | ) | = | 9co | 2 | θ 2 | . | cos | 2 | θ = 2 | 2 | − | 1) |
|
|||||||||||||||||||||||||||||||||||||||||||
| ⎜⎝ | n |
|
. | Δ | violet | = | θ violet | = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | arccos | 1 | ( | n | 2 | − | 1) | = | arccos |
|
1 | (1.342 | 2 | − | 1) |
|
= | 71.55° | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| θ 2 | = | arccos | 1 | ( | n | 2 | − | 1) | = | arccos | 1 | (1.330 | 2 | − | 1) |
|
= | 71.94 . | Δ | red | = | 230.1° and | θ red | = | 50.1 . | ||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EVALUATE: The angles we calculated agree with those given in Figure 37.20e in the textbook.The color that appears higher above the horizon is violet. The colors appear in reverse order in a secondary rainbow compared to a primary rainbow.
