Lateral strain elena pasternak slide lec notes
Expectations on preparation for practical sessions (for students)
The preparation required for practical sessions is to read and revise the preceding lecture notes, visualiser notes and practical session solutions from the previous week.
Example 2.11
A compression bar having a square cross-section of width b must support load P=35kN. The two parts of the bar are connected by a glued joint (known as a scarf joint) along plane pq, which is at an angle α=40 degrees to the vertical.The bar is constructed of a structural plastic for which the allowable stresses in compression and shear are 7.5 MPa and 4 MPa
respectively. The allowable stresses in the glued joint are 5.2 MPa in compression and 3.4 MPa in shear.
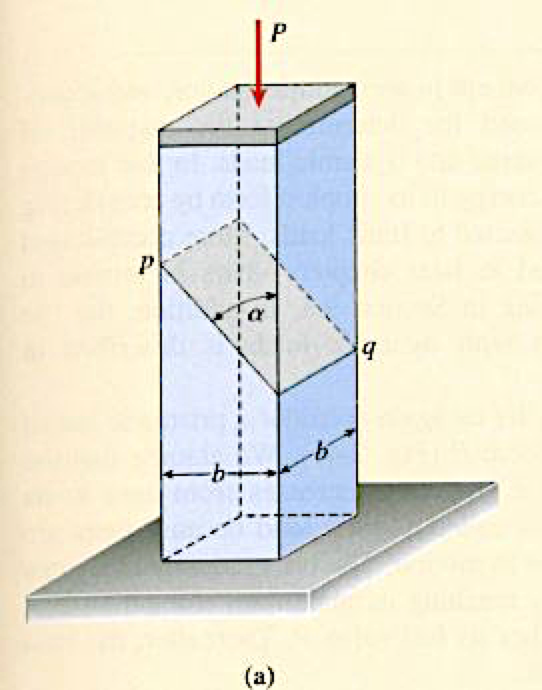
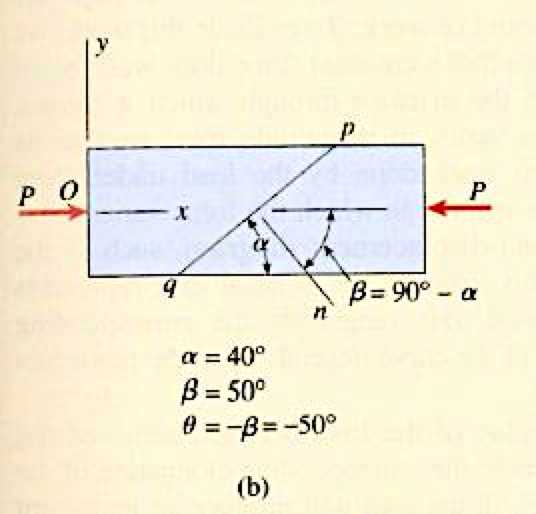

Gere and Goodno (2009)
Dr Elena Pasternak Slide 5


Dr Elena Pasternak Slide 8
Poisson’s ratio ν=0.3.
1 GPa=109Pa
e)The increase in the volume of material ΔV
f)The volumetric strain (dilatation) e
To work on this problem you need to revise lec notes 1 sl 31,32 (normal strain)
sl 35,36 (volumetric strain, dilatation)
sl 45 (Poisson’s ratio, Young’s modulus, lateral strain)Dr Elena Pasternak Slide 11
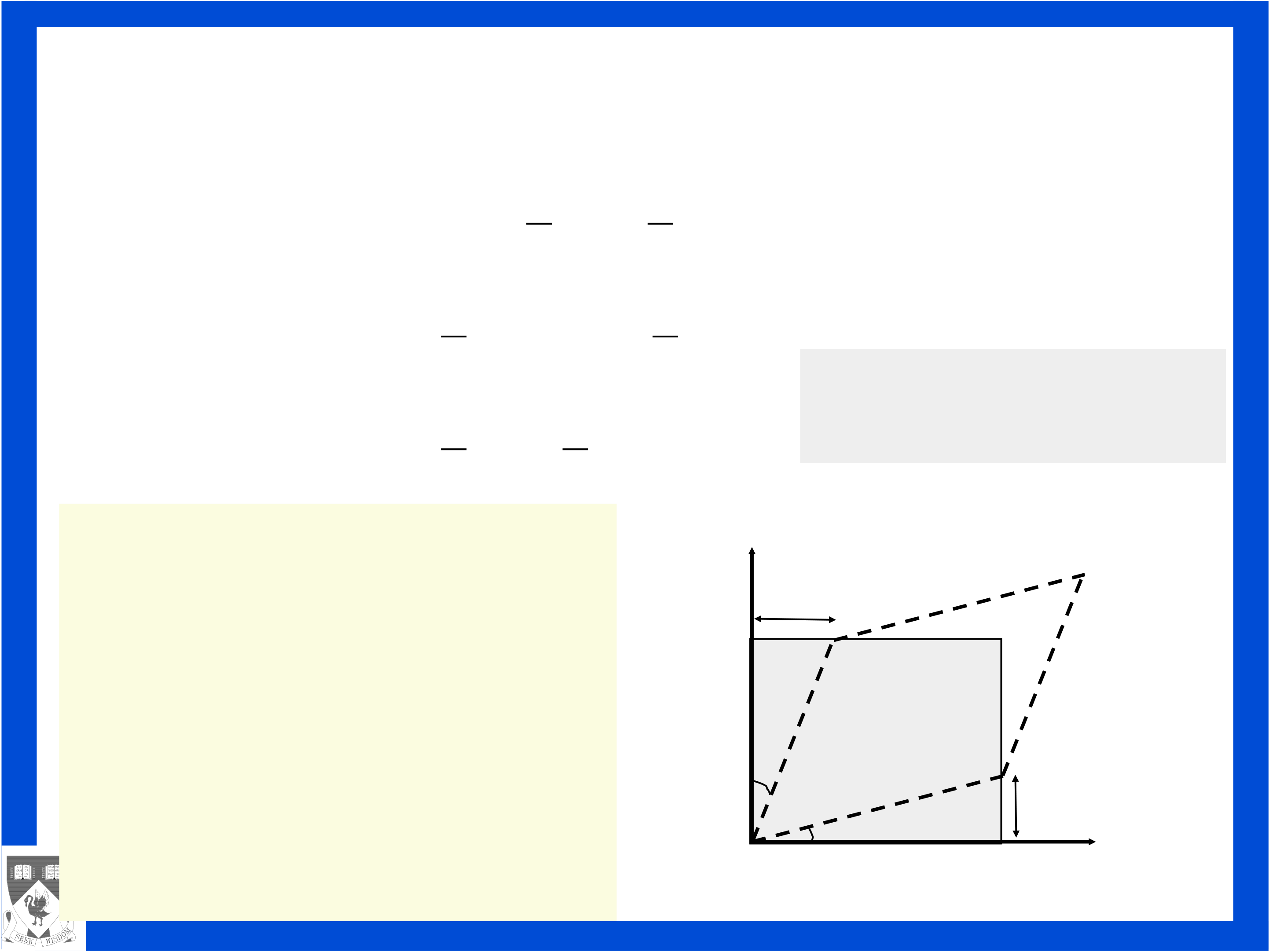
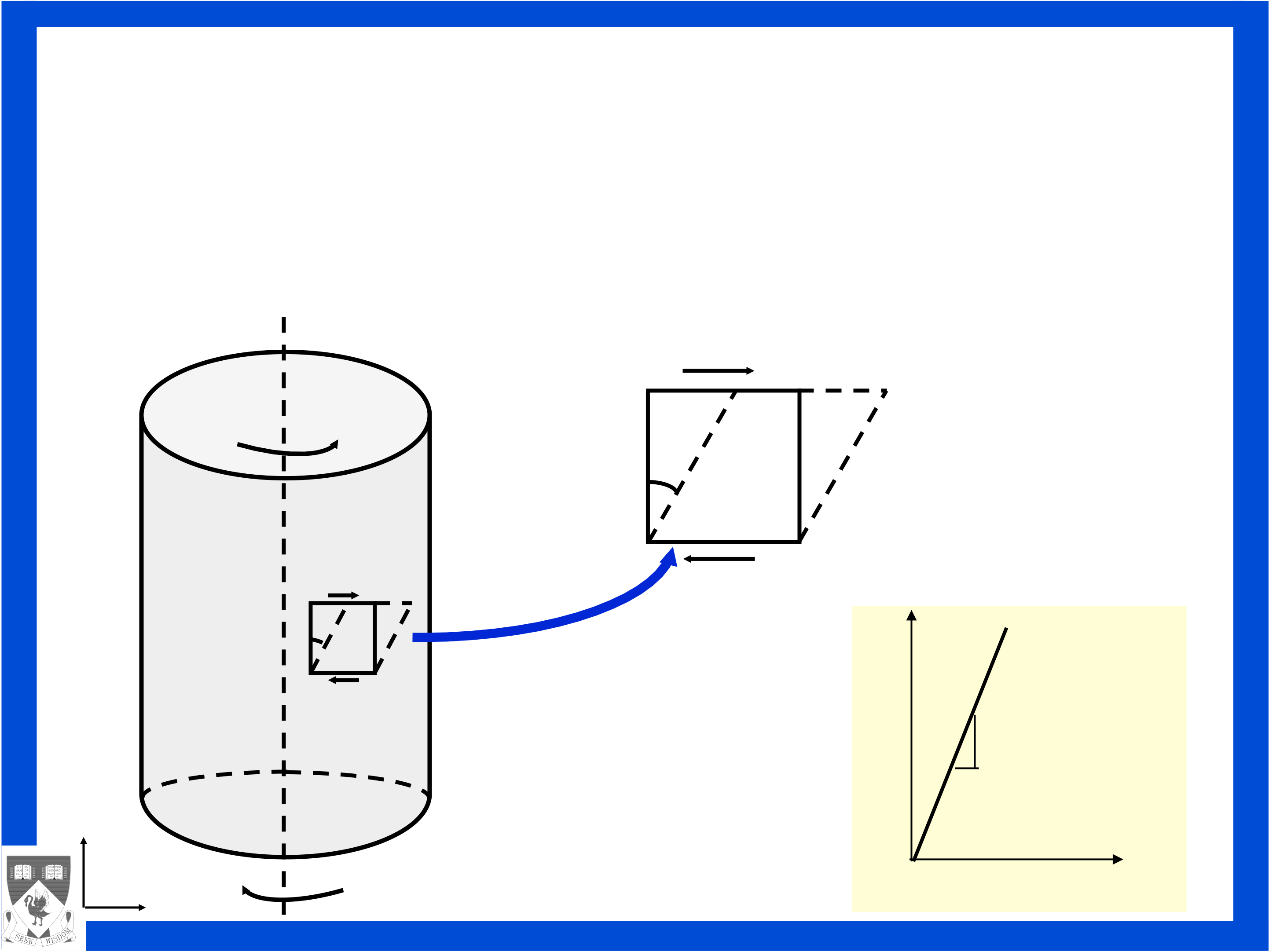
Interpretation of the small deformation. Diagonal terms
length. Diagonal terms of the linear (small) strain tensor
represent normal strains in the coordinate directions.
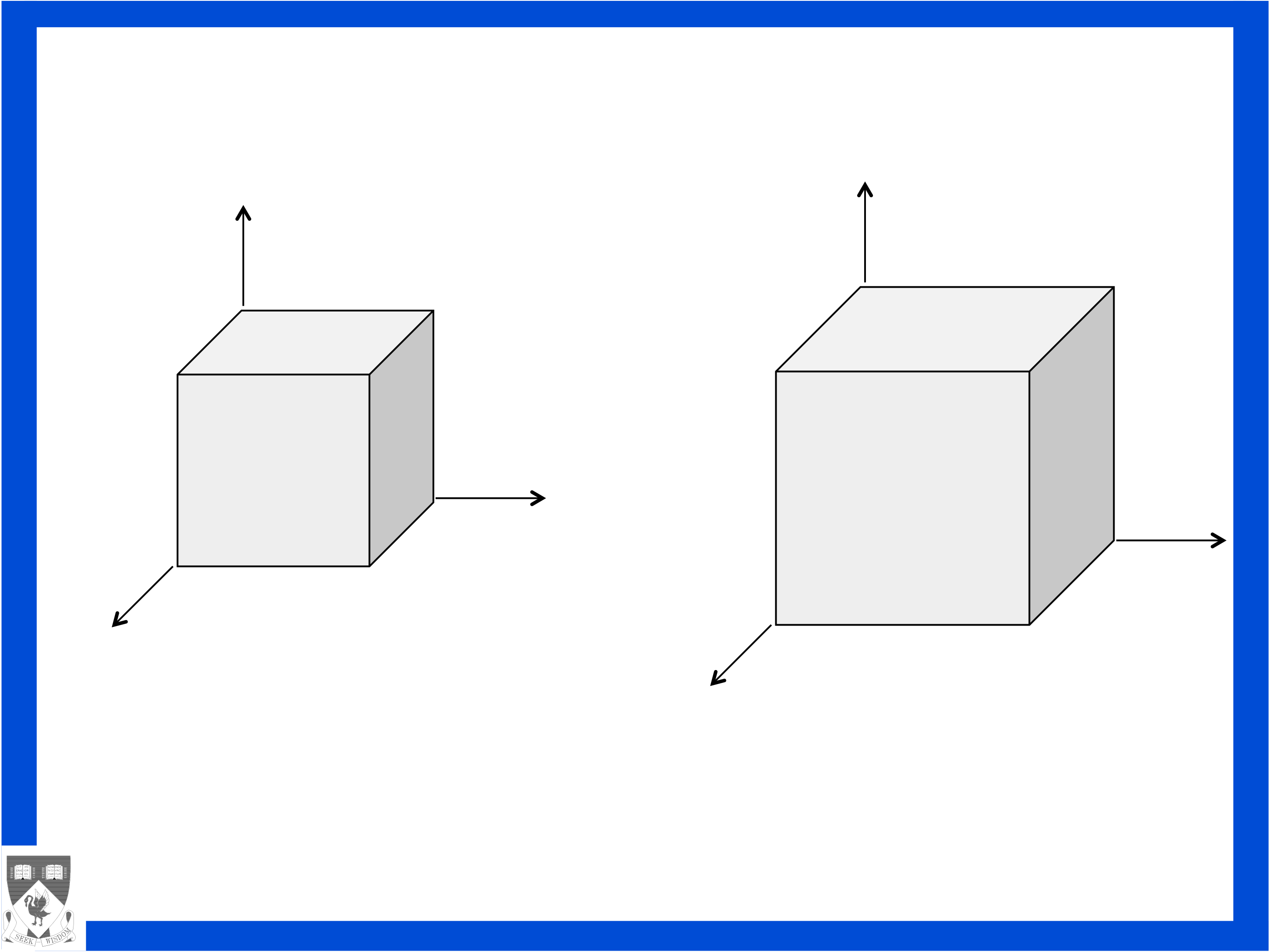
Volumetric strain. Dilatation
| c | x3 | a | x2 | x3 | x2 |
|---|
Volume before deformation: V0=abc
The unit volume change (change in volume per unit volume) is defined as the change in volume divided by the original volume or
This quantity e is also known as volumetric strain and dilatation.
Dr Elena Pasternak Slide 17
Measuring elastic constants
| P | ε |
|
|---|---|---|
Dr Elena Pasternak Slide 21


3. Shear strain
Problem 1.6.
Gere and Goodno (2009)
Dr Elena Pasternak Slide 25

Dr Elena Pasternak Slide 27
31
21
εε
ε
12
1
2
11
γ
γ 32
2
1
α1+α2=γ12 – the change in the
right angle between the line x2 ∂u1/∂x2 elements dx1 and dx2,
“engineering shearing strains”(1/2)(α1+α2)=(1/2)γ12=ε12 – α2
Off-diagonal terms ( ε12, ε21, ε13, ε31, ε23, ε32) of the linear (small) strain represent one-half the angle change between two line elements originally at right angles to one another. Off-diagonal terms of the linear (small) strain tensor represent shear (shearing) strains in the coordinate directions.
Strains are dimensionless [εij]=1.

Small deformation. Infinitesimal strain
| ∂u i |
|
||
|---|---|---|---|
| ∂x |
|
||
Measuring elastic constants.


4. Generalised Hooke’s law. Hydrostatic pressure.
Bulk modulus
40mm
| x3 | 80mm | 60mm |
|
|---|
Dr Elena Pasternak Slide 38

Hydrostatic stress (isotropic extension)
Dr Elena Pasternak Slide 41


Problem 2.10
A rectangular block of material with shear modulus (modulus of rigidity) G=600 MPa is bonded to two rigid horizontal plates. The lower plate is fixed, while the upper plate is subjected to a horizontal force P.Knowing that the upper plate moves through 0.8mm under the action force, determine
a)The average shear strain in the material
b)Force P exerted on the upper plate.


Solution

Problem 2.5
A circle of diameter d=200mm is scribed on an unstressed aluminum plate of thickness t=18mm. Forces acting in the plane of the plate cause normal stresses σxx=85MPa and σzz=150MPa.
Beer et al (1992)
Dr Elena Pasternak Slide 48

Dr Elena Pasternak Slide 50
| = | ε | ij | = | + | ν | σ | ij | − | ν | δ | ij | σ | kk | = | 1 | + | ν | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
E | ||||||||||||||||||||||||||||||||||
| 1 |
|
− | ν | σ | 22 | − | ν | ||||||||||||||||||||||||||||
| E | ε 13 | ||||||||||||||||||||||||||||||||||
| ⎪ | |||||||||||||||||||||||||||||||||||
| = | − | ν | σ 11 | + | 1 |
|
22 | − | ν | σ |
|
||||||||||||||||||||||||
| 22 | |||||||||||||||||||||||||||||||||||
| E | E | ||||||||||||||||||||||||||||||||||
| = | − | ν | σ 11 | − | ν | σ | 22 | + | 1 |
|
|
||||||||||||||||||||||||
| 33 | |||||||||||||||||||||||||||||||||||
| E | E | E | |||||||||||||||||||||||||||||||||
| ⎪ | 1 | + | ν | σ 12 | ε | 23 | = | 1 | + | ν | 23 | , | |||||||||||||||||||||||
| = | |||||||||||||||||||||||||||||||||||
⎪ε 12 ⎩ |
|||||||||||||||||||||||||||||||||||
| E | E | E | |||||||||||||||||||||||||||||||||
Solution
Dr Elena Pasternak Slide 53
»Was consultation/Extra practical session class on Friday useful?
Dr Elena Pasternak Slide 54
