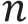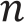Multiply the series the common ratio and subtract the original
Sequences and series
Sequences and series – A guide for teachers (Years 11–12)
Full bibliographic details are available from Education Services Australia.
Published by Education Services Australia
PO Box 177
Carlton South Vic 3053
Australia
Australian Mathematical Sciences Institute
Building 161
The University of Melbourne
VIC 3010
Email: enquiries@amsi.org.au
Website: www.amsi.org.au
Sequences . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Series . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Use of induction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Telescoping series . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
History and applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
An application to film and video . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Sequences
and seriesAssumed knowledge
are examples. We can ‘predict’ what the 20th term of each sequence will be just by using common sense.
Another sequence of great historical interest is the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Sequences can be either finite or infinite. For example,
2, 4, 6, 8, 10
• Can we find a formula for the general term of the sequence?
• Does the sequence have a limit, that is, do the numbers in the sequence get as close as we like to some number?
2+4+6+8+···+20
is the series formed from the sequence 2,4,6,8,...,20.An infinite series is the ‘formal sum’ of the terms of an infinite sequence. For example,
If it exists, this limit is often referred to as the limiting sum of the infinite series. In this module, we examine limiting sums for one special but commonly occurring type of series, known as a geometric series.
Sequences and series are very important in mathematics and also have many useful ap-plications, in areas such as finance, physics and statistics.
1, 3, 5, 7, 9, ...
is an example of a typical infinite sequence. The dots indicate that the sequence con-tinues forever, with no last term. We will use the symbol an to denote the nth term of a given sequence. Thus, in this example, a1 = 1, a2 = 3, a3 = 5 and so on; the first term is a1 = 1, but there is no last term.
• write out the first few terms
• give a formula for the general term
A much better way to describe a sequence is to give a formula for the nth term an. This is also called a formula for the general term. For example,
an = 2n −1
| a1 = 1 | and |
|---|
The initial term is a1 = 1, and the recurrence tells us that we need to add two to each term to obtain the next term.
The Fibonacci sequence comprises the numbers
Write down the first five terms of this sequence.
b the sequence 1,4,9,16,... of squares.
In general, however, finding a formula for the general term of a sequence can be difficult. Consider, for example, the Fibonacci sequence:
| an =1 5 | ��1+ 2�5 | �n | − | �n� |
|---|
This is a very surprising result! (It is not even obvious that this formula will give an integer result for each n.) You might like to check that this formula works for n = 1,2,3.
{8} • Sequences and series
where each term is obtained from the preceding one by adding a constant, called the common difference and often represented by the symbol d. Note that d can be positive, negative or zero.
Thus, the sequence of even numbers
2, 4, 6, 8, 10, ...
|
|---|
Exercise 3
Find the nth term of the arithmetic sequencelog5 2, log5 4, log5 8, ... .
| Exercise 4 |
|---|
Geometric sequences
A geometric sequence has the form
a, ar, ar2, ar3, ...in which each term is obtained from the preceding one by multiplying by a constant, called the common ratio and often represented by the symbol r. Note that r can be pos-itive, negative or zero. The terms in a geometric sequence with negative r will oscillate between positive and negative.
{10} • Sequences and series
Exercise 5
Find the nth term of the geometric sequence
|
|---|
|
|---|
|
We often use the sigma notation for series. For example, if we have the series 2+4+6+···+100
in which the kth term is given by 2k, then we can write this series as
|
or |
|
|---|
{12} • Sequences and series
| k=1 n� |
|
|---|
This is sometimes called the nth partial sum of the infinite series.
an = Sn −Sn−1 = n2−(n −1)2= 2n −1.
So the terms form the sequence of odd numbers. Hence, we have found a formula for the sum of the first n odd numbers:
A guide for teachers – Years 11 and 12 • {13}
The series
1+2+3+···+n
is an arithmetic series with common difference 1. There is an easy way to find the sum of this series. We write the series forwards and then backwards:
For example,
2×100×101 = 5050. 1+2+3+···+100 =1
Legend has it that the famous mathematician Gauss discovered this at the age of nine! This ‘trick’ works for any arithmetic series, and gives a formula for the sum Sn of the first n terms of an arithmetic series with first term a1 = a and last term an = ℓ. The formula is Sn =n�a +ℓ� .Exercise 7
Use the method of writing the arithmetic series
| Sn =n | �2a +(n −1)d�. |
|
|---|---|---|
| =n | ||
| =n |
|
|---|
Exercise 8
Sum the arithmetic serieslog2 3+log2 9+log2 27+···
to n terms.
A guide for teachers – Years 11 and 12 • {15}
We can find a formula for the sum of the first n terms of this series, again using a little trick. We multiply the series by the common ratio 4 and subtract the original, as follows.
This ‘trick’ works for any geometric series, and gives a formula for the sum Sn of the first n terms of a geometric series with first term a and common ratio r. The formula is
| Sn =a(r n −1) r −1 | , |
|
|---|
Use the method of multiplying the geometric series
a + ar + ar2+···+ arn−1
{16} • Sequences and series
|
|---|
It is a simple matter to find the average of two numbers. For example, the average of 6 and 10 is 8. When we do this, we are really finding a number x such that 6,x,10 forms an arithmetic sequence. In general, if the numbers a,x,b form an arithmetic sequence, then
| a= b x, | giving | x = | � |
|---|
|
|---|
One of the many applications of sequences and series occurs in financial mathematics. Here we will briefly discuss compound interest and superannuation.
Compound interest
Depreciation is closely related to compound interest. When a company, for example, buys a car for work-related purposes, it is able to claim the depreciation in the value of the car over time as a tax deduction.
Superannuation
Superannuation is a way of saving for retirement. Money is regularly invested over a long period of time and (compound) interest is paid. Suppose I invest in a superannuation scheme for 30 years which pays 6% per annum. I put $3000 each year into the scheme, and (for the sake of simplicity) we will suppose that the interest is added yearly.
This example illustrates both the value of regular saving and the power of compound interest. The $90000 invested becomes roughly $251400 over 30 years.
The limiting sum of a geometric series
| n→∞Sn = lim n→∞ | a(1−rn) 1−r | = |
|
|---|
The value of this limit is called the limiting sum of the infinite geometric series. The values of the partial sums Sn of the series get as close as we like to the limiting sum, provided n is large enough.
|
|---|
A guide for teachers – Years 11 and 12 • {21}
In general, the limiting sum of an infinite series a1 +a2 +a3 +··· is the limit, if it exists, of the sequence of partial sums S1,S2,S3,..., where
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
and so on. Infinite series are often written in the formLinks forward
Use of induction
is hardly obvious and requires a proof. While the Greeks had some very creative proofs of results such as this, the best approach is to give a proof using mathematical induction.
{22} • Sequences and series
Telescoping series
Most series are neither arithmetic nor geometric. Some of these series can be summed
1+1 2+ 1 3+ 1 4+ 1 5+··· .
There is no simple expression for the sum of the first n terms of this series. Does the series have a limiting sum? The following argument shows that the answer is no.
| � | + | � 1 16+ 1 16+···+ 1 16 | � |
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| ≥ 1+1 2+ | �1 4+ 1 | � | + | �1 8+ 1 8+ 1 8+ 1 | |||||
| = 1+1 2+ 1 2+ 1 2+ 1 2+··· , | |||||||||
which grows without bound. So the harmonic series does not have a limiting sum.
Connection with integration
Integration is used to find the area under a curve. We can approximate the area under the curve by rectangles, and add up the areas of the rectangles. This gives a finite series. By taking more rectangles of smaller width, we obtain a series that better approximates the area. We can define the area under the curve to be the limit of the sequence of sums, provided the limit exists.
| 0 | – 1 | 1 |
|
|---|
| An =1 | �� 1 | �2 | + | � 2 | �2 | +···+ | �n |
|---|
n rectangles L1,L2,...,Ln:
| Bn =1 | �� 0 | �2 | + | � 1 | �2 | +···+ | �n −1 |
|
|---|
Since Bn ≤ Area R ≤ An, we now have
| 3− 1 2n+ | 6n2 ≤ Area R ≤ 1 3+ 1 2n+ | 1 6n2 . |
|---|
By taking the limit as n → ∞, we see that the area of R is1 3. We can take this as the definition of the area of R.
respectively. In general, if a1,a2,...,an are n positive real numbers, their arithmetic and geometric means are
|
and |
|---|
{26} • Sequences and series
The harmonic mean H of two positive numbers a and b is defined by
| H= 1 | � 1 a+ 1 |
|---|
| H= 1 | � 1 a1 | +1 a2 | +···+1 an |
|
|---|
The AM–GM inequality
| ≥ | � |
|---|
a Find the arithmetic, geometric and harmonic means of 3,4,5 and write them in as- cending order.
b Prove that the harmonic mean of two positive real numbers a and b is less than or equal to their geometric mean.
| ≥ |
|---|
Exercise 16
An application to film and video
In modern film and video, one has the power to vary the width and height of the images being filmed and replayed. The ratio between the width and height of an image is called its aspect ratio. This ratio is commonly expressed in the form x : y.
The Fibonacci sequence
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
| a1 = a2 = 1 | and |
|---|
A first-order linear recurrence such as an = kan−1, where k is a constant, is easily seen to have the solution an = a1 ×kn−1, which is an exponential. By taking A =a1 k, we can write the solution as an = A kn.
One approach to solving a second-order linear recurrence is to guess an exponential so-lution of the form an = A kn, where A and k are non-zero constants. Substituting this into the recurrence for the Fibonacci sequence, we have
| an = A1 × | �n | + A2 × |
|
�n |
|
|---|
The Greeks defined several different means. Less well known is the Heronian mean N(a,b) of two positive real numbers a and b, which is the average of the three numbers a, b and their geometric mean. That is,
| N(a,b) =a +b + | � | ab |
|
= | � | |
|---|---|---|---|---|---|---|
|
||||||
and
| � | ab ≤ N(a,b) ≤a +b |
|---|
That is, the Heronian mean lies in between the geometric and arithmetic means.
Again, we can generalise and define the Heronian mean N of n positive real numbers a1,a2,...,an to be
{30} • Sequences and series
but they also introduced the sequence of triangular numbers 1, 3, 6, 10, ...
 |
 |
 |
|||
| T1 = 1 | |||||
The first four triangular numbers.
The Greeks used geometric techniques to show that
12+22+32+···+n2=1 6n(n +1)(2n +1)
and
13+23+33+···+n3=1 4n2(n +1)2 = (1+2+3+···+n)2.
Exercise 3
The sequence simplifies to
log5 2, 2log5 2, 3log5 2, ...and so the general term is an = n log5 2.
| Exercise 5 | |||||
|
|||||
| We have a = | = | �6(�2)n−1= | |||
Exercise 7
Writing the series forwards and backwards, we have
| Sn = | a | + | (a +d) | + | (a +2d) | + | ··· | + | (ℓ−d) | + |
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sn = | ℓ | + | (ℓ−d) | + | (ℓ−2d) | + | ··· | + | (a +d) | + |
Exercise 9
We have
Sn = a + ar + ar2+···+ arn−1
rSn = ar + ar2+···+ arn−1+ arn.
| rSn −Sn = arn− a | =⇒ | |||
|---|---|---|---|---|
| =⇒ | , | |||
{32} • Sequences and series
Exercise 11
| a | |||||
|---|---|---|---|---|---|
| X Y= X Y | =⇒ | � | |||
b Let C be the midpoint of AB. Let D be the point where the perpendicular to AB at C cuts the semicircle. Then CD is the radius of the semicircle, and so CD =1 Clearly, CD ≥ X Y , and therefore1 2(a +b) ≥�ab. 2(a +b).
Exercise 12
Exercise 13
Exercise 14
which is the arithmetic mean of logb a1, logb a2, ..., logb an. =1�logb a1 +logb a2 +···+logb an�,
A guide for teachers – Years 11 and 12 • {33}
| a | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HM= 1 |
|
� |
|
||||||||
| b | � | =⇒ | |||||||||
|
|||||||||||
| HM =2ab a +b≤ 2ab ab | = | � | |||||||||
| (a1a2 ...an) | n ≤ A =a1 + a2 +···+ an |
|
|---|
which is the desired result.