Now create the google matrix enter the formula cell
Maths delivers!
Google PageRank
© The University of Melbourne on behalf of the Australian Mathematical Sciences Institute (AMSI), 2013 (except where otherwise indicated). This work is licensed under the Creative Commons
Attribution-NonCommercial-NoDerivs 3.0 Unported License. 2011.http://creativecommons.org/licenses/by-nc-nd/3.0/

maths delivers!
2 This list of web pages is ordered, so that (hopefully) the pages most useful to you will be at the top of the list.
Google’s success at performing this second step has played a major role in making it the world’s favourite search engine.
A web page’s popularity score is also called its Google PageRank. In these notes, which accompany the maths delivers! video of the same name, we explain how the PageRank of a web page is calculated, and we discuss some of the mathematics which guarantees that the calculation actually works.
The PageRank formula was presented to the world in Brisbane at the Seventh World Wide Web Conference (WWW98) by Sergey Brin and Larry Page, the founders of Google, in 1998. That year, Larry Page filed a patent for their pro-cess to calculate the PageRank of web pages, and the patent was granted in 2001. The rest is
The basic idea
We would like to attach a number to each web page that represents its importance.
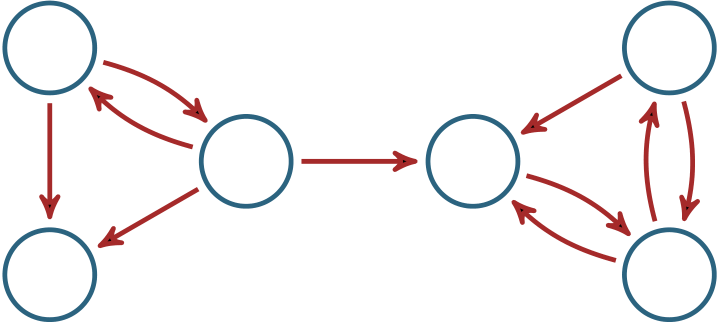
The graph W in figure 2 is the hyperlink graph of a system of six web pages. We can see, for example, that there are outlinks from page P3 to pages P1, P2 and P4, and that P2 has inlinks from pages P1 and P3 but has no outlinks at all.
The hyperlink matrix
The graph W shown in figure 2 is encoded in the 6×6 table on the left in figure 3: the cell in row Pi, column P j contains a 1 if there is a link from page Pi to page P j, and contains a 0 otherwise.
The PageRank equations
How do we measure the importance of a page? A link from your page to my page is an endorsement of my page. The more inlinks my page has, the more important it is. However, some links are more valuable than others.
| • |
|
|---|
For our six-page ‘mini web’, this leads to the following PageRank equations:
We are searching for a PageRank row vector
| r(Pi) = | P j ∈LPi� |
|---|
8 ■ maths delivers!
The PageRank equations via matrices
|
|
|
1 | 1 | 0 | 0 | 0 | |
|---|---|---|---|---|---|---|---|---|
| 2 | 2 | |||||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 1 | 0 | 1 | 0 | 0 | ||||
| =�r(P1) r(P2) r(P3) r(P4) r(P5) r(P6)� | | 3 | 3 |
|
||||
|
0 | 0 | 0 | 0 | 1 | |||
| 0 | 0 | 1 | 0 | 1 | ||||
| | 2 | 2 | ||||||
| 0 | 0 | 1 | 1 | 0 | ||||
| 2 | 2 |
v = v H.
It would be easy to solve our six PageRank equations by hand. There is also a systematic method for solving such a system of simultaneous equations (the Gaussian algorithm) which can be carried out by a computer.
For the initial approximation v(0), they take all pages to have the same PageRank. For our‘mini web’ example, we have
A Is there a theorem that guarantees the sequence v(0),v(1),v(2),v(3),... will converge to a vector v?
B If the sequence v(0),v(1),v(2),v(3),... converges to a vector v, will v necessarily be a probability vector?
| v(0)= | �1 6, 1 6, 1 6, 1 6, 1 6, 1 |
|---|
10 ■ maths delivers!
Figure 5: The Excel spreadsheet using H.
| v = | �0, 0, 0, 1 5, 2 15, 4 15 | |
|---|---|---|
The problem is caused by the row of zeros in the matrix H. This row of zeros corresponds to the fact that P2 is a dangling node, that is, it has no outlinks. Dangling nodes are very common in the World Wide Web (for example: image files, PDF documents, etc.), and they cause a problem for our random web surfer. When Webster enters a dangling node, he has nowhere to go and is stuck.
To overcome this problem, Brin and Page declare that, when Webster enters a dangling page, he may then jump to any page at random. This corresponds to replacing each row of 0’s in the matrix H by a row of1 n’s, where n is the total number of nodes in our graph. This new matrix S is called the stochastic matrix of the graph W , as each row sums to 1.
v(k+1)= v(k)S
to calculate v(1),v(2),v(3),.... Using Excel, we obtain the results shown in figure 7.
| P_1 | P_2 | P_3 | P_4 | P_5 | P_6 | |
|---|---|---|---|---|---|---|
| v^(0) | 0.16666667 | 0.16666667 | 0.16666667 | 0.16666667 | 0.16666667 | 0.16666667 |
| v^(1) | 0.08333333 | 0.16666667 | 0.11111111 | 0.25000000 | 0.11111111 | 0.27777778 |
| v^(2) | 0.06481481 | 0.10648148 | 0.06944444 | 0.25925926 | 0.16666667 | 0.33333333 |
| v^(3) | 0.04089506 | 0.07330247 | 0.05015432 | 0.29089506 | 0.18441358 | 0.36033951 |
| v^(4) | 0.02893519 | 0.04938272 | 0.03266461 | 0.30131173 | 0.19238683 | 0.39531893 |
| v^(5) | 0.01911866 | 0.03358625 | 0.02269805 | 0.31297154 | 0.20588992 | 0.40573560 |
| v^(6) | 0.01316372 | 0.02272305 | 0.01515704 | 0.31897648 | 0.20846551 | 0.42151420 |
| v^(7) | 0.00883952 | 0.01542138 | 0.01036904 | 0.32382938 | 0.21454428 | 0.42699641 |
| v^(8) | 0.00602658 | 0.01044634 | 0.00698999 | 0.32679692 | 0.21606843 | 0.43367174 |
| v^(9) | 0.00407105 | 0.00708434 | 0.00475434 | 0.32894114 | 0.21857693 | 0.43657219 |
| v^(10) | 0.00276550 | 0.00480103 | 0.00321625 | 0.33034006 | 0.21946682 | 0.43941033 |
| v^(11) | 0.00187226 | 0.00325501 | 0.00218292 | 0.33131083 | 0.22050534 | 0.44087365 |
| v^(12) | 0.00127014 | 0.00220627 | 0.00147863 | 0.33195963 | 0.22097932 | 0.44210600 |
| v^(13) | 0.00086059 | 0.00149566 | 0.00100278 | 0.33240325 | 0.22142071 | 0.44281701 |
| v^(14) | 0.00058354 | 0.00101383 | 0.00067957 | 0.33270240 | 0.22165778 | 0.44336288 |
| v^(15) | 0.00039550 | 0.00068726 | 0.00046074 | 0.33290583 | 0.22185041 | 0.44370026 |
| v^(16) | 0.00026812 | 0.00046587 | 0.00031229 | 0.33304346 | 0.22196467 | 0.44394558 |
| v^(17) | 0.00018174 | 0.00031580 | 0.00021171 | 0.33313687 | 0.22205043 | 0.44410344 |
| v^(18) | 0.00012320 | 0.00021407 | 0.00014351 | 0.33320014 | 0.22210436 | 0.44421472 |
| v^(19) | 0.00008351 | 0.00014512 | 0.00009728 | 0.33324305 | 0.22214304 | 0.44428800 |
| v^(20) | 0.00005661 | 0.00009837 | 0.00006594 | 0.33327213 | 0.22216819 | 0.44433876 |
| v^(21) | 0.00003838 | 0.00006668 | 0.00004470 | 0.33329185 | 0.22218577 | 0.44437262 |
| v^(22) | 0.00002601 | 0.00004520 | 0.00003030 | 0.33330521 | 0.22219742 | 0.44439585 |
| v^(23) | 0.00001763 | 0.00003064 | 0.00002054 | 0.33331427 | 0.22220546 | 0.44441146 |
| v^(24) | 0.00001195 | 0.00002077 | 0.00001392 | 0.33332041 | 0.22221083 | 0.44442211 |
| v^(25) | 0.00000810 | 0.00001408 | 0.00000944 | 0.33332457 | 0.22221451 | 0.44442929 |
| v | 0 | 0 | 0 | 1/3 | 2/9 | 4/9 |
which is a probability vector since
3+ 2 9+ 4 9= 1.
Guaranteeing that the limiting vector exists
There is a simple modification to the matrix S that will simultaneously answer ques-tions A and C: We will be guaranteed that the sequence of vectors v(0),v(1),v(2),v(3),... converges to a positive vector v.
each row r of the matrix S by
|
|---|
In their original 1998 paper, Brin and Page state that they usually set d = 0.85. With this
| | 1 | 9 | 9 | 1 | 1 | 1 | | ||
|---|---|---|---|---|---|---|---|---|---|
| | 40 | 20 | 20 | 40 | 40 | 40 | | ||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 6 | 6 | 6 | 6 | 6 | 6 | ||||
| 37 | 37 | 1 | 37 | 1 | 1 | ||||
| G = | | 120 | 120 | 40 | 120 | 40 | 40 | | |
| 1 | 1 | 1 | 1 | 1 | 7 | ||||
| | 40 | 40 | 40 | 40 | 40 | 8 | | ||
| 1 | 1 | 1 | 9 | 1 | 9 | ||||
| | 40 | 40 | 40 | 20 | 40 | 20 | | ||
| 1 | 1 | 1 | 9 | 9 | 1 | ||||
| | 40 | 40 | 40 | 20 | 20 | 40 | | ||
v(k+1)= v(k)G
to calculate v(1),v(2),v(3),.... Using Excel, we obtain the results shown in figure 8.
v = (0.0517, 0.0737, 0.0574, 0.2800, 0.1851, 0.3521).
This allows us to rank our six web pages in order from most important to least important
| 6th | 5th | 2nd | |
|---|---|---|---|
| 4th |
Google PageRank ■ 15
The calculation of PageRanks for our example involves a 6×6 matrix. However, the cal-culation by Google of PageRanks for the entire World Wide Web involves a matrix that is more than 14 billion by 14 billion! The reason that this calculation is even possible is that the Google matrix G is based on the original hyperlink matrix A, which is sparse (mean-ing that most of its entries are zeros). If there are n web pages, then the matrix A has n2 entries. On average, a web page has only 10 outlinks, and so there are approximately 10n non-zero entries in the matrix A. As the number of web pages n is extremely large, the number 10n is very much smaller than n2.
Using the formula in 2b above, we obtain the following table.
| Digits of accuracy | Iterations required |
|---|---|
16 ■ maths delivers!
To illustrate the independence of the limiting vector v from the starting vector, we can
Figure 10: The Excel spreadsheet using G: new v(0).
Google PageRank ■ 17
| � | first 10-digit prime found in consecutive digits of e |
|---|
Figure 11: The Google advertisement.
If you found the password and logged in, you landed on the Google recruiting page shown in figure 12, and you had an invitation to apply for a job with Google.
18 ■ maths delivers!
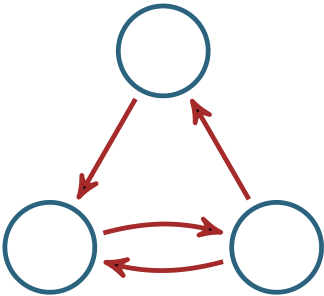
















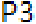

Google PageRank ■ 19
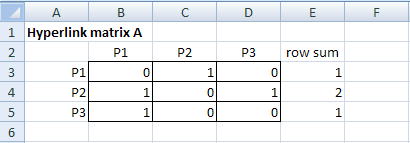
Figure 13: Baby web example.
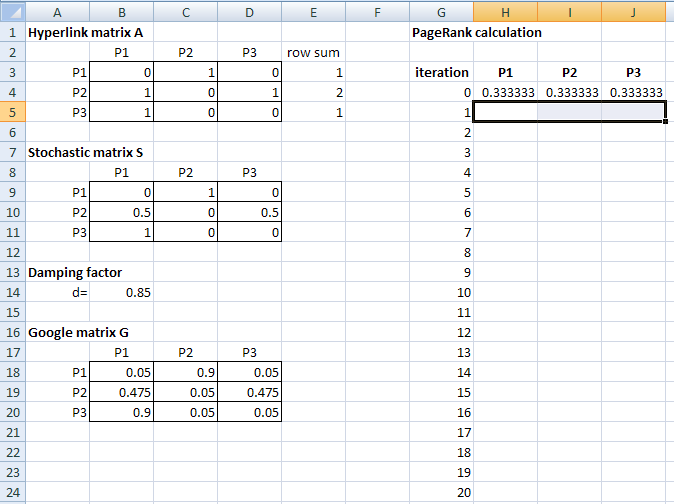
Step 1: The hyperlink matrix. In an Excel spreadsheet, enter the hyperlink matrix A that corresponds to the graph, as shown in the following screenshot. The row sums have been calculated by entering the formula =SUM(B3:D3) in cell E3 and then dragging down to cell E5.
Step 3: The Google matrix. Enter the value 0.85 into cell B14; this will be the damping
factor. Now create the Google matrix: Enter the formula
|
We’re nearly ready to perform the iteration to solve the Page- |
|---|---|
|
|
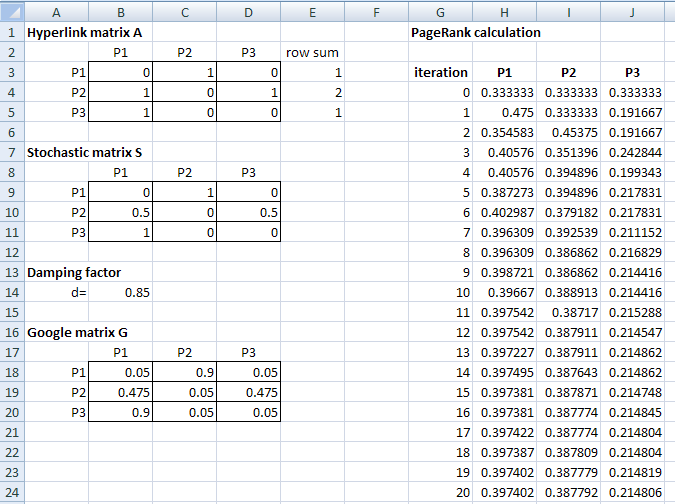
Figure 17: Preparation for the iteration.
and 0.215, respectively.
• changing the hyperlink matrix A to correspond to a different three-node graph W .
Using a similar process, you can also set up a spreadsheet to check the calculations for
• Amy N. Langville and Carl D. Meyer, Google’s PageRank and Beyond: The Science of
Search Engine Rankings, Princeton University Press, 2006.