Refractive index in terms of real depth and apparent depth
GEOMETRICAL OPTICS
Remember to photocopy 4 pages onto one sheet by going A3→A4 AND back to back on the photocopier
Contents
How our brain determines the position of an object 8
How an image is formed in a plane mirror* 9
Convex mirrors – ray diagrams 14
The science of learning quiz: Part 3 25
Applications of total internal reflection 31
Leaving Cert Physics syllabus: Refraction 38
Why does a converging lens cause light to converge? 45
Convex (converging) lenses - ray diagrams 45
GEOMETRICAL OPTICS EXAM QUESTIONS 2002 – 2022 63
Optical fibres: Ordinary level 67
Optical fibres: Higher level 68
Introduction to the science of learning
Isn’t it strange that despite students being in a learning environment between the ages of 4 and 24, teaching students how to learn isn’t a core part of classroom teaching at all levels?
“There is an overwhelming assumption in our educational system that the most important thing to deliver to students is content” (p. 341, italics in original). One concern here is that students who do well in earlier grades, in which learning is largely supervised, may struggle later, when they are expected to regulate much of their own learning, such as in high school or college. Teaching students to use these techniques would not take much time away from teaching content and would likely be most beneficial if the use of the techniques was consistently taught across multiple content areas, so that students could broadly experience their effects on learning and class grades.
The word “truthiness” was coined to describe an intuitive feeling that an idea just “feels right,” even if there is in fact no evidence for it. Ineffective study techniques are a perfect example of this; they feel so right that we think they must be useful. Unfortunately not.
There are just a two key ideas that I want you to learn from this series of lessons:
The science of learning quiz: Part 1
One of the least well-known study techniques is known as ‘pre-testing’. It turns out that if you take a test even before you study the material it seems to prime the brain so that it recognises and pays more attention to the concepts when it encounters them again in the normal fashion. So we’re going to apply that here. You’re going to attempt each of the questions below. You need to write down your best guess for each question (even if you have absolutely no idea what it’s about) and after you have attempted them you can check your answers on the next page.
What if we could remember everything?
https://www.youtube.com/watch?v=bSycdIx-C48
In the later 1960’s American psychologists Richard Atkinson and Richard Shiffrin discovered that memory formation can be divided into three different stages. Name each stage and explain each term.
Answers
What is amnesia?
The woman who could not forget - 6 minute YouTube video
So the challenge is to teach our brain to forget what we don’t need and to remember what we do need. It would be nice if the rule it used was; “remember what I want to remember” but unfortunately that’s not it. If it was then we wouldn’t keep forgetting our passwords or whether or not we turned on the alarm as we left the house. So how does it decide what information to keep and what to discard?
Storing the information for future use in the brain’s long term memory.
Retrieving the information: getting it back out from the brain’s long term memory.
Between 4 and 7. What implications does this have for how you study?
What is the difference between short-term memory and working memory?
1. PLANE MIRRORS
Something to think about
Draw a diagram of a book sitting on a table with a stick person standing on the floor beside the table, and a light-bulb higher up.
Show, using arrowed lines on the diagram, how the person sees the book.Is it possible to build an instrument which would allow you to see yourself being born – or conceived?
How far away would this instrument have to be in order to allow you to see dinosaurs roaming the Earth?
Student Notes
Reflection is defined as the bouncing of light off an object
When light hits off most everyday objects it scatters in all directions – this is known as diffuse reflection, but when the surface it shines off of is flat and silvered – a plane mirror – then it behaves in a much more predictable way.
Laws of reflection of light*
Note the angle of incidence is the angle between the incident ray and the normal (not from the mirror), and the angle of reflection is the angle between the reflected ray and the normal.
The normal in turn is an imaginary line perpendicular to the surface.
How our brain determines the position of an object
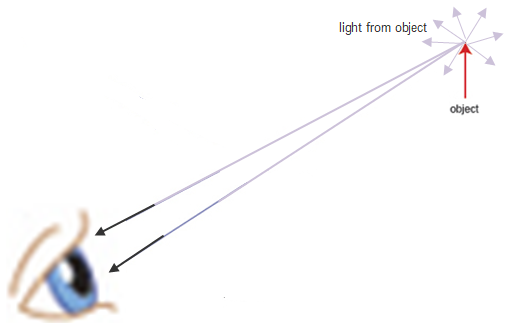
Even more impressive is that the same process works on just one eye (monocular vision) – see the image for how it works.
Now close one eye and repeat.
It’s much trickier. It’s impressive that we can do it at all when you think about it. But then I don’t suppose you have ever thought about it before.
How an image is formed in a plane mirror*
The image formed by a plane mirror is called a ‘virtual image’ *
This is pretty cool
Our brain normally figures out how far away an object is by analysing diverging rays as they hit the two eyes and assuming that the object’s position is located where the lines intersect.
This usually works, except when the diverging light is coming back off a mirror.
Because of the geometry involved, the rays appear to intersect as far behind the mirror as the object is in front.
We will verify this by experiment shortly.
The science of learning quiz: Part 2
Answers
What are the greatest misconceptions that students (and many parents) have about learning?
All that matters is how long you spend studying
By the way, why is this idea (that all that’s important is the time spent studying) so pervasive?
The act of retrieving information from your long term memory makes it easier to recall again in the future. This obviously doesn’t happen with a video-tape (5:00 in the video below).
A video tape has limited capacity. Your long-term memory has almost infinite capacity and the more you learn the more space you create because you are storing concepts that can be used to create links to further related information (4:00 in the video below).
We may laugh at how silly this is, but the practice of believing that your brain will store the information just because you read it isn’t much different.
2. SPHERICAL MIRRORS
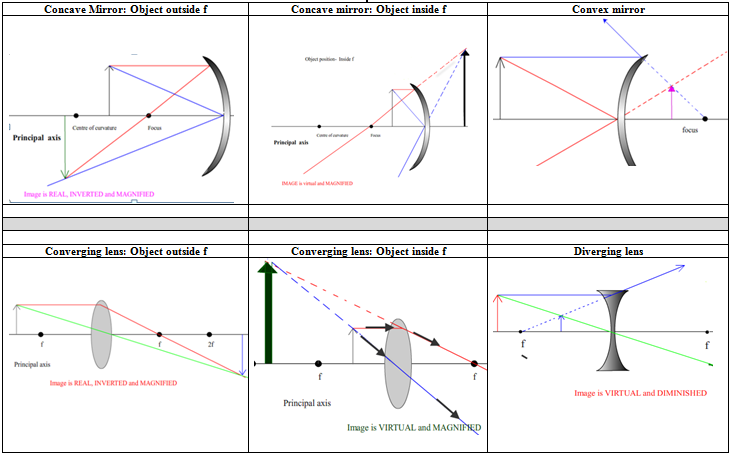
Concave mirrors – ray diagrams
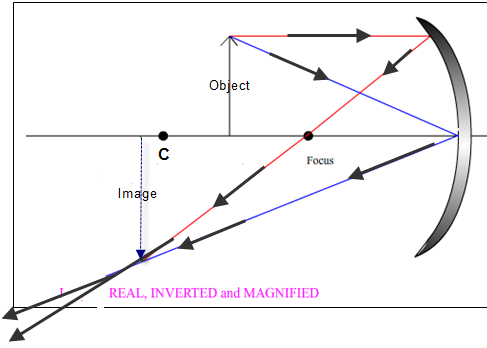
Rays of light which strike a concave mirror reflect back in a predictable way. Here we will refer to just two or three rays of light which reflect back in a manner which is easy to remember.
And once again the position where these lines intersect represents the position of the image (or, in the case of a virtual image, where the brain thinks the image is located).
From top of object to mirror (parallel to principal axis); back through the focus.
From top of object, hitting the mirror on the principle axis and back out at same angle on the other side.
Just put a very slight curvature on the mirror to begin with, or better still make the mirror a straight line while drawing the rays, and only afterwards put in a slight curve.
Put arrows on all rays – do this for all the images below

Object inside the focus
A real image is an image formed by the actual intersection of light rays.
A real image can be located on a screen.
A virtual image is always behind the mirror and upright.
Uses of concave mirrors
Searchlights
Point 4 – Cosmetic mirrors; if your face/tooth inside the focus the image is magnified and upright.
Convex mirrors – ray diagrams
Here only one diagram is needed; the image is always diminished, upright and virtual.
Notice that in this situation (similar to the concave mirror when the object is inside the focus) the light rays never intersect, but from the viewer’s perspective they appear to do so behind the mirror.
The image is therefore always virtual, regardless of where the object is placed.
Uses of convex mirrors
Maths problems
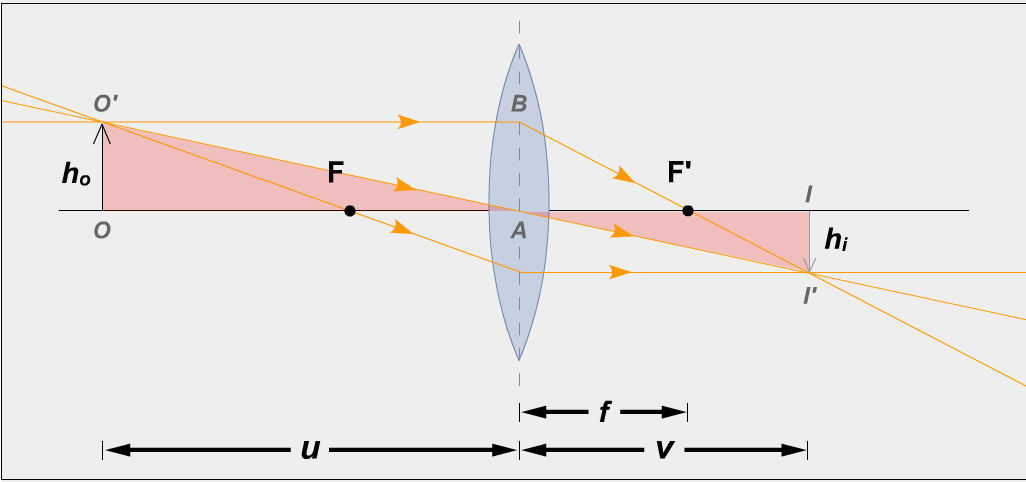
Relationship between focal length (f), object distance (u) and image distance (v) for spherical mirrors
Which is the object distance; U or V?
object distance u = 30 cm |
$\frac{\mathbf{1}}{\mathbf{f}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{u}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{v}}$ $\frac{\mathbf{1}}{\mathbf{20}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{30}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{v}}$ $\frac{\mathbf{1}}{\mathbf{20}}\mathbf{-}\frac{\mathbf{1}}{\mathbf{30}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{v}}$ $\frac{\mathbf{1}}{\mathbf{60}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{v}}$ Answer: v = 60 cm |
Magnification
Magnification refers to the ratio of the height of the image to the height of the object (if the image is 2 times higher than the object then the magnification is 2. It turns out that the image height to object height is the same as the ratio of the image distance to the object distance)
Calculate the image distance.
Solution
| $$M = \frac{image\ height}{object\ height} = \ \frac{3}{2} = 1.5$$ | |
|---|---|
M = 1.5 v = ? |
$M = \ \frac{v}{u}$ (M)(u) = v (1.5)(17) = v v = 25.5 cm |
Calculate the distance from the object to the mirror.
A person looks at her image in a shiny spherical decoration when her
face is 30 cm from the surface of the decoration. The diameter of the
decoration is 20 cm.
Find the position of the image.
Solution |
|
|---|---|
f = 5 cm u = 30 cm |
|
MANDATORY EXPT: Measurement of the focal length of a concave mirror
APPARATUS: Concave mirror, screen, lamp-box with crosswire, metre stick, retort stand.
Measure the distance between the mirror and the screen.
This corresponds to an approximate value for the focal length of the mirror.
Repeat this procedure for different values of u.
Calculate the focal length of the mirror using the formula
and get an average.
Parallax error associated with measuring u and v; ensure your line of sight is at right angles to the metre stick.
Take all measurements from the back of the mirror.
Related Exam Questions
“I placed an object at different positions in front of the mirror so that a real image was formed in each case.” The table shows the measurements recorded by the student for the object distance u and the image distance v.
| Theory questions | |
|---|---|
Draw a labelled diagram showing how the apparatus was arranged. |
|
| Calculate the value for the focal length f of the mirror using the data. | |
| How was an approximate value for the focal length found? | |
| What was the advantage of finding the approximate value for the focal length? | OR so a real image could be formed |
| Describe how the student found the position of the image. | The position of the screen was adjusted until the image of the cross-wires came into focus. |
| Give two precautions that should be taken when measuring the image distance. | Avoid parallax error when measuring distances, measure to back of mirror, sharp image formed |
| Explain why the student was unable to form an image on the screen when the object was close to the mirror. | The object was inside the focal length / virtual image formed |
| Why did the student repeat the experiment? | To improve the overall accuracy |
Extra reading
You are therefore looking back in time!
Now if you look up at the night sky you can see objects which are so far away that it has taken light millions of years to reach us.
To begin with, bear in mind that most of the material in a ‘mirror’ is not actually there for reflection. The glass part is there to act as protection for the reflective metal backing, as well as to prevent oxidation (rusting). Therefore when measuring distances to or from a mirror, the front of the metal backing should be used to represent the position of the mirror.
You might have noticed that the incident ray of light seems to bend somewhat as it passes in and out of the glass. This is an important phenomenon and is called refraction. We deal with it in detail in Chapter 4.
I really think that to appreciate this you’ve got to look at the image of a (lighting) candle through a sheet of plane glass and try to get the image to ‘stand’ in a beaker of water placed behind the glass.
This phenomenon was used quite a bit in the theatre (in conjunction with mirrors) to make images appear out of thin air.
Note
Demonstrating this experiment is not on the syllabus and therefore cannot get asked on the Leaving Cert exam.
This may sound straightforward to a physics professor, but trust me; it makes little sense to a sixteen year-old student who (if you have ever thought about it at all) would have thought that the image is in the mirror.
The misconception arises because, although our brain is indeed fooled into thinking that the image is behind the mirror, we quickly come to realise as infants that there is actually nothing behind there. From then on we accept that the image is (apparently) in the mirror. This is worth a class discussion in itself to try and sort out the confusion.
Because it’s a real image it means it sits there in mid-air. You don’t generally notice images in mid-air because the light forming the image is swamped by background light. But if you cover off this background light by using a screen then the image becomes visible.
This image in turn acts like a real object in that it can be magnified further, which is how microscopes work; it really is quite impressive. If you are a teacher you need to purchase a ‘Mirage Mirror’ – see www.sciplus.com. for about €30.
Use a concave mirror to form an image of a distant object on a sheet of A4 paper. Try to use a colourful object – the colour image is impressive – can you notice anything else about it?
Use the ray-box and a slit which forms three parallel rays of light to reflect off of the mirror. What do you notice?
Leaving Cert physics syllabus: Mirrors
SLOP
| Test yourself by covering the answers | |
|---|---|
| What is meant by the reflection of light? | Reflection is defined as the bouncing of light off an object |
| State the laws of reflection of light. | |
| Use a ray diagram to show the formation of a real image by a concave mirror. | |
| Use a ray diagram to show the formation of a virtual image by a concave mirror. | 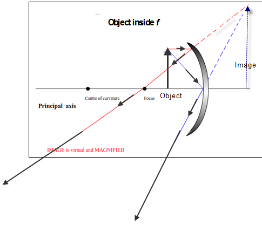 |
| Use a ray diagram to show the formation of an image by a convex mirror. | 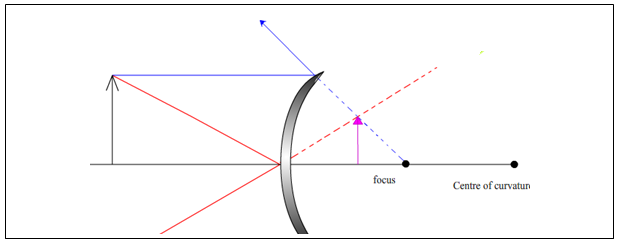 |
| Describe the image that is formed in a concave mirror when an object is placed inside the focus. | The image is virtual, magnified and upright. |
| Describe the image that is formed in a concave mirror when an object is placed outside the focus. | The image is real and inverted. |
| Describe the image that is formed in a convex mirror. | The image is virtual, diminished and upright. |
| Give two uses for a concave mirror. | Torch, headlights, searchlight, dentist mirror, cosmetic mirror, solar furnace. |
| Give two uses for a convex mirror. | At concealed entrances to give a view of oncoming traffic |
| Give one difference between a real image and a virtual image. | Real image can be obtained on a screen; virtual image cannot. |
| Concave mirrors, rather than convex mirrors, are used by dentists to examine teeth. Explain why. | They give a magnified image |
| Why is a convex mirror used, instead of a plane mirror, as a door mirror on a car? | A convex mirror offers a wider field of view |
| An object O is placed 30 cm in front of a concave mirror of focal
length 10 cm. How far from the mirror is the image formed? |
⇒ 1/v = 1/10 - 1/30 ⇒ v = 15 cm = 0.15 m |
| A concave mirror has a focal length of 20 cm. An object is placed 30
cm in front of the mirror. How far from the mirror will the image be formed? |
|
The science of learning quiz: Part 3
What is the Dunning-Kruger effect?
Recap:
What is meant by the term ‘illusions of competence’?
It is very common for a student to develop a false sense of mastery of the material which can in turn lead to over-confidence. This can happen when you are watching a teacher go through a problem on the board which seems to make sense, but then when you’re asked to repeat it yourself you quickly realise that you don’t actually understand it after all. It can also happen when you highlight or ‘look over’ material instead of using a more reliable study technique like ‘elaborative interrogation’ which we will come across later.
What is the Dunning-Kruger effect?
This is the effect whereby the less we know about a subject, the less competent we are to judge whether we know it or not. In other words the very fact that we know very little about the subject is likely to make us overly confident. Which isn’t ideal if we have a test on that subject the following day.
1 minute explanation from John Cleese on YouTube
Slightly longer (5 minute) YouTube video
Retrieving the information: getting it back out from the brain’s long term memory.
How can we ‘encode’ information when we first encounter it?
Back to the physics . . .
3: REFRACTION
Something to think about
Refraction is the bending of a wave as it passes from a medium of one refractive index to another medium of different refractive index.
Strictly speaking only some of the light passes through to the second medium; the rest of it gets reflected back. The reflected ray is known as the weak reflected ray. To make life simple we pretend that the reflected ray doesn’t exist.
Laws of refraction of light
The ratio of the sin of the angle of incidence to the sin of the angle of refraction is a constant called the refractive index.
The refractive index between any two media is a constant and is given the symbol ŋ.
2018 Question 5 [Ordinary level]
Calculate the refractive index of the glass block shown in the diagram.
Critical angle
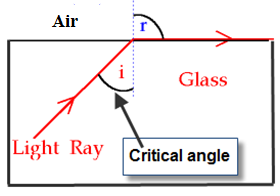 The diagram shows a ray of
light inside a glass block striking the glass/air
interface.
The diagram shows a ray of
light inside a glass block striking the glass/air
interface.
Relationship between critical angle and refractive index
Students looking for a H1 should be able to show where this formula comes from.
Solution
$n = \frac{1}{\sin c} = \ \frac{1}{\sin{41.8}} = \frac{1}{0.67}$
|
|
|---|---|
2015 Question 5 [Higher Level] |
|
207 Question 5 [Higher Level] The refractive index of a liquid is 1.35, what is the critical angle of the liquid? |
$n_{g} = \frac{1}{\sin C}$ $\sin C = \frac{1}{n_{g}}$ $\sin C = \frac{1}{1.35}$ $C = \sin^{- 1}\frac{1}{1.35}$ ⇒ C = 47.80 |
Applications of total internal reflection
Reflective road signs
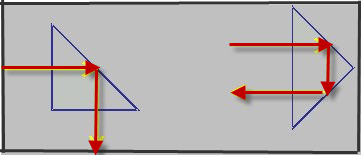
Optical fibres*
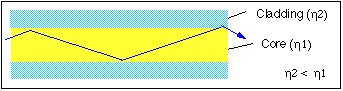
This process continues all along the glass pipe until the light emerges at the far end.
Note:
Telecommunications
Medicine (endoscopes)
Refractive index in terms of the speed of light in different media
Or
Note that the speed of light is 3×108 m s-1 (that’s 300 million metres per second, or 300 000 km per second!)
(speed of light in air = 3.0 × 108 m s–1) |
|
|---|
| Speed of light in air = 3 × 108 m s-1 | Speed of light in glass = $\frac{distance}{time} = \ \frac{5500\ \times \ 10^{3}}{29\ \times \ 10^{- 3}}$ = 1.9 × 108 m s-1 |
|---|---|
| $n = \ \frac{c_{air}}{c_{glass}} = \ \frac{3 \times 10^{8}}{1.9 \times 10^{8}}$ = 1.58 | |
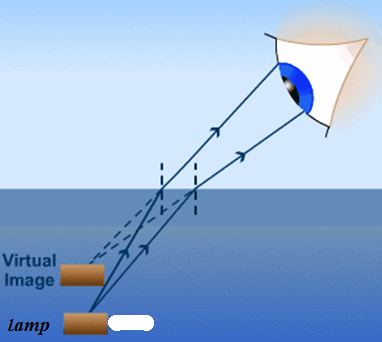
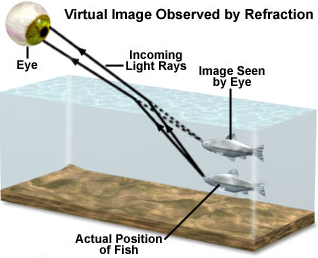
Refractive index in terms of real depth and apparent depth
Refraction explains why a swimming pool is deeper than it actually appears to be.
 2019 Question 12
(c)
2019 Question 12
(c)
2011 Question 12 (b) [Higher Level]
Summary of formula
$$\mathbf{R.I. =}\frac{\mathbf{Real\ Depth}}{\mathbf{Apparent\ Depth}}$$
 And remember boys and
girls . . .
And remember boys and
girls . . .
MANDATORY EXPT: Verification of Snell’s law of refraction
DIAGRAM (I couldn’t find one which included the ray-box)
PROCEDURE
Measure the angle of incidence i and angle of refraction r using the protractor.
Repeat for different values of i.
The refractive index of glass is also equal to the average value of $\frac{\sin i}{\sin r}$
RESULTS
Start with a small angle of incidence and measure the corresponding angle of refraction.
Now increase this angle at roughly regular intervals each time to ensure a wide range of values (rather than simply taking angles at random each time).
Related exam questions
| Theory questions | |
|---|---|
Diagram to show: Glass block |
|
| What measurements were taken during the experiment? | Angle of incidence and angle of refraction |
| Describe how the student found the path of the ray of light passing through the glass block. | |
| Describe, with reference to the diagram, how the student found the angle of refraction. | By measuring the angle between the normal and the refracted ray using a protractor. |
| Draw a suitable graph to illustrate the relationship between the angle of incidence and the angle of refraction. | Sin i on vertical axis, sin r on horizontal axis. Correct sin i and sin r values for six points |
| Use your graph to find the refractive index of the material. | The slope of the graph corresponds to the refractive index of the material. |
| Explain how your graph verifies Snell’s law. | Straight line through the origin shows that sin i is proportional to sin r |
| The student did not record any values of i below 20°, why not? | There would be a greater percentage error associated with measuring smaller angles. |
| What would be observed if the incident ray was perpendicular to the block? | The light ray would go straight through (would not be refracted). |
| Using a graph to calculate a value for the refractive index is a more accurate method than calculating the refractive index for each pair of angles and then finding the mean. Give a reason for this. | Any errors can be more easily identified on a graph than in a table of data as the associated point will be well off the line so can be ignored. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Leaving Cert Physics syllabus: Refraction
A note on the mandatory experiments
But in verifying Snell’s Law, we plot a graph of Sin i against Sin r, and show that because the graph is a straight line going through the origin, the two variables are directly proportional.
To calculate the refractive index we then simply calculate the slope of the graph, and if Sin i is on the y-axis, the slope corresponds to the refractive index.
Extra reading
There is then the issue of what type of density the definition is referring to; is it mass/volume, is it optical density or is it density of electrons (given that the movement of light is affected by electric fields associated with electrons).
*Snell’s Law
But I ask again – how does light know how much to bend by?
See the related link in the refraction page of thephysicsteacher.ie
Why is "c" used for the speed of light?
From the Latin 'celeritas', meaning speed, as an alternative to v (for particles).
Never again ask why God invented Carlow.
Rainbows are formed as a result of sunlight undergoing total internal reflection in drops of rain
SLOP
| Snell | |
|---|---|
| What is meant by refraction of light? | The bending of light as it passes from one medium to another medium of different refractive index. |
| State Snell’s law of refraction. | The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant. |
| State the laws of refraction of light. | The incident ray, the refracted ray and the normal all lie in the same plane. Sin i/ Sin r is a constant |
| What is meant by the refractive index of a material? | n = sin i/ sin r, where i is the angle of incidence and r is the angle of refraction. |
| Explain, with the aid of a diagram, how total internal reflection can occur. | |
| Define the term total internal reflection. | Total internal reflection occurs when the angle of incidence in the denser of the two media is greater than the critical angle and light is reflected back into the denser medium. |
| When will total internal reflection occur? | When the angle of incidence is greater than the critical angle. |
| Define the term critical angle. | The critical angle corresponds to the angle of incidence in the denser of two media which causes the angle of refraction to be 900. |
| The critical angle for the glass is 42o. Calculate the refractive index of the glass. |
$n_{g} = \frac{1}{\sin C}$ $n_{g} = \frac{1}{\sin 42^{0}}$ $n_{g} = \frac{1}{0.669}$ ⇒ n = 1.49 |
| The refractive index of a liquid is 1.35, what is the critical angle of the liquid? | |
| Calculate the critical angle for diamond. The refractive index of diamond is 2.4. |
|
| What is the critical angle of a sample of glass whose refractive index is 1.46? | $n_{g} = \frac{1}{\sin C}$ $\sin C = \frac{1}{n_{g}}$ $\sin C = \frac{1}{1.46}$ sin C=0.685 C = sin−10.685 C = 43.20 |
| Give two uses of total internal reflection. | Fibre optics, endoscopes, reflective road signs, telecommunications, binoculars, periscope. |
| Show how a prism can be used to rotate light through 1800. | |
| Draw a diagram to show the path of a ray of light travelling through an optical fibre. | |
| Explain how a signal is transmitted along an optical fibre. | |
| How is the escape of light from the sides of an optical fibre prevented? | Total internal reflection occurs due to an outer cladding of lower refractive index. |
| An optical fibre has an outer less dense layer of glass. What is the role of this layer of glass? | Total internal reflection will only occur if the outer medium is of lower density. It also prevents damage to the surface of the core. |
| Give one use for optical fibres. | Endoscope, telecommunications, binoculars. |
| Give two reasons why the telecommunications industry uses optical fibres instead of copper conductors to transmit signals. | Less interference, boosted less often, cheaper raw material, occupy less space, more information carried in the same space, flexible for inaccessible places, do not corrode, etc. |
cglass = 3.0 × 108/1.55 cglass = 1.94 × 108 m s-1 |
|
|
|
| Name a material that is used in the manufacture of optical fibres. | Glass / plastic / sand / silicon |
The science of learning quiz: Part 4
What is the significance of the phrase “Memory is the residue of thought” in relation to study skills?
This follows on from the previous question. Long term memories are formed as the residue of thought. In other words, you need to be thinking about the material in order to remember it.
Were you ever sent to pick up just three items from the shop and end up only thinking of two? You didn’t write them down because you knew that you wouldn’t forget. Or come up with a new password that you know that you’re never going to forget, and one you really ‘want’ to remember, only to have forgotten it next time you go to log into that website?
The Science of Thinking: 11 minute YouTube video from Veritasium
‘Elaborative interrogation’ is an excellent (but not widely used) study technique. What is meant by this term?
When recall is easy, learning is low.
We feel clever when we recall something instantly but in terms of getting our brain to store information we should feel the exact reverse. It’s as if your brain assumes that if it had to work hard to remember something then that ‘something’ must be important, so it stores it even more securely for the future.
4: LENSES
Why does a converging lens cause light to converge?
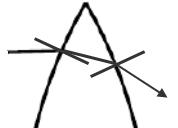 Look at the image on the right,
where the ray of light is coming in from the left hand side.
Look at the image on the right,
where the ray of light is coming in from the left hand side.
At the first interface the light ray is travelling from a medium of low refractive index to a medium of higher refractive index and so bends towards the normal. The opposite happens at the second interface (light ray bends away from the normal). You should try this exercise for yourself, but this time work with the bottom half of the lens so see the direction of the emergent ray.
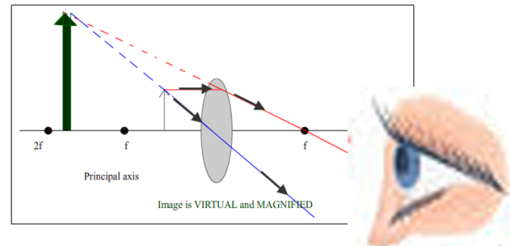
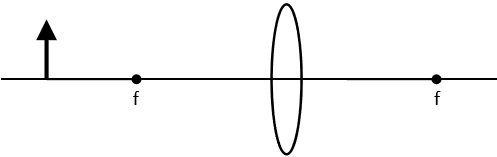
Convex (converging) lenses - ray diagrams
inside the focus – resulting in a virtual image
Two Rules
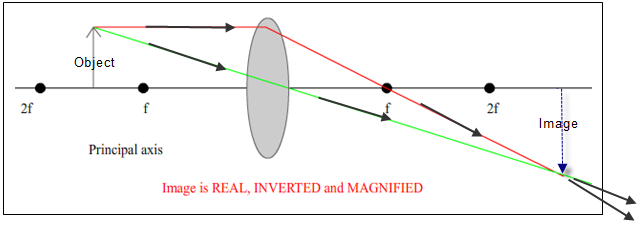

Note
A real image is always on the other side of the lens (to the object) and is inverted.
Concave (diverging) lenses - ray diagrams
From the top of the object to the lens, parallel to principle axis and up as if coming from the focus.
 From the top of the object to
centre of lens and continue straight through.
From the top of the object to
centre of lens and continue straight through.
Summary of all ray diagrams (for both mirrors and lenses)
Maths Problems
Relationship between focal length (f), object distance (u) and image distance (v)
If you are looking for v and it turns out to be positive, it means that the image is a real image.
If you are looking for v and it turns out to be negative, it means that the image is a virtual image.
Magnification refers to the ratio of the height of the image to the height of the object (if the image is 2 times higher than the object then the magnification is 2.
It can be shown that this ratio is the same as the ratio of the image distance to the object distance v:u)
Calculate the image distance, v.
Calculate the magnification, m.
The eye*
Optic Nerve – carries the information in electrical form to the brain
Iris – acts like a shutter to control the amount of light entering the eye
Short sightedness
A short-sighted person can see nearby objects clearly but cannot bring distant objects into focus.
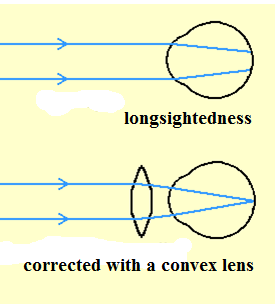
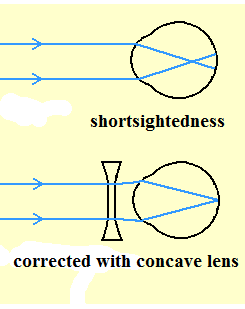
Power of a lens*
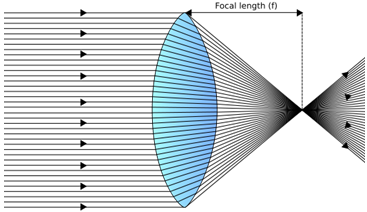 The power of a lens is simply
the reciprocal of the focal length of the lens. We use it because it
allows us to calculate the effect of having two lenses next to each
other, where one is the lens in a short-sighted or long-sighted eye and
the other is a corrective lens.
The power of a lens is simply
the reciprocal of the focal length of the lens. We use it because it
allows us to calculate the effect of having two lenses next to each
other, where one is the lens in a short-sighted or long-sighted eye and
the other is a corrective lens.
Remember to use the correct sign convention because a converging lens will have the opposite effect as a diverging lens.
Convention
A certain person’s eye has a power of 62 m–1.
The lens of their glasses has a power of –2 m–1.
2002 Question 12 (b) [Higher Level]
State the laws of refraction of light.
Calculate the focal length of the contact lens required to correct the person’s short-sightedness.
2008 Question 9 [Higher Level]
Calculate how near an object can be placed in front of the eye and still be in focus;
Calculate the maximum power of the internal lens.
Why does the cornea not act as a lens?
What is the maximum power of the eye?
A converging lens is used as a magnifying glass.
Draw a ray diagram to show how an erect image is formed by a magnifying glass.A diverging lens cannot be used as a magnifying glass. Explain why.
Full revision question
2019 Question 11 [Ordinary Level]
Adapted from https://science.howstuffworks.com/innovation/everyday‐innovations/lens6
Name the part of the eye where an image is formed.
 Copy the diagram below into
your answerbook and complete the ray diagram to form a real
image.
Copy the diagram below into
your answerbook and complete the ray diagram to form a real
image.The power required to clearly view a nearby object is 38 m‐1.
A person with an eye defect has a maximum power of 32 m‐1.
Calculate the power of the lens required to correct this defect?
What is the focal length of this lens?
Mandatory EXPT: Measurement of the focal length of a convex lens
PROCEDURE
First find an approximate value for the focal length.
Move the screen until a clear inverted image of the crosswire is obtained.
Measure the distance u from the crosswire to the lens, using the metre stick.
| Object distance u | ||||||
|---|---|---|---|---|---|---|
| Image distance v | ||||||
| Focal Length f |
SOURCES OF ERROR / PRECAUTIONS
Determining when the image was in sharpest focus; repeat each time and get an average.
Related exam questions
Use all of the data to calculate the focal length of the converging lens.
|
||||||||||||||||||||||||||||||
Leaving Cert Physics syllabus: Lenses
| Content | Depth of Treatment | Activities | STS |
|---|---|---|---|
| Lenses | Knowledge that 1/f = 1/v + 1/u |
Simple exercises on lenses by ray tracing or use of formula. | Use of lenses |
| m = v/u | |||
| Power of lens: P = 1/f | |||
| The eye: Optical structure, short sight, long sight, and corrections. | Spectacles | ||
Extra reading
Why?
Answer
Can you explain why?
Answer
Close one eye and look at the cross with the open eye – can you still see the black dot “out of the corner of your eye”?
Now slowly move your head towards the cross. Notice that at one
particular distance the black dot disappears out of the corner of your
eye but then reappears as you move in closer still.
Why?
Look into the eyes of another student beside you while the room is suddenly darkened – what do you notice about their ‘eyeballs’? The effect is even more impressive (for obvious reasons) is you go from dark to brightness. Can you explain why?
Answer
What would happen if we wore a pair of glasses which made the image on the retina the right way up?
Answer
Did you know that a TV screen shows 24 pictures a second? Because a fly sees 200 images a second, it would see TV as still pictures with darkness in between.
Confusion with Mirrors and Lenses
The water forms droplets on the leaves. These droplets act as converging lenses and focus the sun onto the leaves, burning them. As a result the leaves will have brown spots. Although this could be a myth; it seems a little strange that millions of years of evolution wouldn’t have corrected for this.
*Power of a lens
n lens = 1.42
n vitreous humour = 1.336
Some historians of art now believe that from the early 15th century many Western artists including Van Eyck, Caravaggio and Vermeer used mirrors and lenses to create living projections.
Optics would have given artists a new tool with which to make images that were both immediate and powerful, enabling them to project colour images onto flat surfaces and then capture these projections in pencil and paint.
This formula often causes confusion:
Note: none of the following has ever been required on any exam questions to date on this topic. However it is on the syllabus so is included here.
But for the record:
The last two lines are what is referred to as the ‘Real is Positive’ convention (RiP).
Remember that for a convex lens the image is only virtual if the object is inside the focus.
I also suggest working the whole sum out in the calculator, rather than trying to find lowest common denominators etc. But this does require being proficient in the use of your calculator!
It is also advisable in this case to show your workings in your answer. This is so that if mess up the calculator work, at lease the examiner can see that you had the right idea.
SLOP
GEOMETRICAL OPTICS EXAM QUESTIONS 2002 – 2022
Mirrors: Ordinary level
 What is meant by reflection
of light?
What is meant by reflection
of light?State the laws of reflection.
2012 Question 12 (b) [Ordinary Level]
State the laws of reflection of light.
 2021 Question 10
[Ordinary Level]
2021 Question 10
[Ordinary Level]
A periscope is used on a submarine. The periscope uses plane mirrors to allow a person on the submarine to see above the surface of the water.
Copy the ray diagram below into your answerbook and complete it to show how a real image is formed in a concave mirror.
State one use of a concave mirror.
State one use of a convex mirror.
Use a ray diagram to show the formation of a real image by a concave mirror.
A concave mirror has a focal length of 20 cm. An object is placed 30 cm in front of the mirror.
How far from the mirror will the image be formed?
 In your answerbook, copy and
complete the ray diagram below to show how a magnified image is formed
in a concave mirror.
In your answerbook, copy and
complete the ray diagram below to show how a magnified image is formed
in a concave mirror.The image formed is real. Explain what is meant by a real image.
Light is also reflected by convex mirrors.
Sketch a convex mirror. Indicate which side of the mirror reflects light.
Mirrors: Higher level
Draw a ray diagram to illustrate how Rembrandt used a concave mirror in this way.
Explain why this image was not of use to Rembrandt.
2014 Question 12 (b) [Higher Level]
Concave mirrors, rather than convex mirrors, are used by dentists to examine teeth. Explain why.
Refraction: Ordinary level
Give an application of reflection of light.
Describe an experiment to demonstrate one of the laws of reflection of light.
In the diagram the value of the angle i is 380.
Calculate the value of the refractive index of the glass.
State the laws of reflection of light.
Describe an experiment to demonstrate one of the laws of reflection of light.
In the diagram the value of the angle i is 41.80.
Calculate a value for the refractive index of the glass.
Explain, with the aid of a labelled diagram, (i) total internal reflection, (ii) critical angle.
The diagram shows a 45o prism made of glass.
The critical angle for the glass is 42o.
Give two uses of total internal reflection.
Refraction: Higher level
Use a labelled diagram to explain why the diver does not appear to be at a depth of 12 m when viewed by an observer outside the pool.
(refractive index of water = 1.33)
Calculate the speed of light as it passes through the glass.
2011 Question 12 (b) [Higher Level]
At night, when the lamp is switched on, a disc of light is seen at the surface of the swimming pool. Explain why the area of water surrounding the disc of light appears dark.
Calculate the area of the illuminated disc of water.
Optical fibres: Ordinary level
Draw a labelled diagram to show how an optical fibre transmits light along its length.
An optical fibre cable has a refractive index of 1.5.
Calculate the angle at which total internal reflection occurs.
(Adapted from New Scientist, 13 October 1990)
(a) Draw a diagram to show how a ray of light is transmitted through an optical fibre.
(f) Define the critical angle.
(g) When will total internal reflection occur?
Give a practical application of the reflection of light.
State the laws of reflection of light.
Optical fibres are also used in medicine. Give an example of their use in medicine.
Optical fibres: Higher level
An optical fibre is manufactured using glass of refractive index of 1.5.
Calculate the speed of light travelling through the optical fibre.
Why is each fibre coated with glass of lower refractive index?
What is the speed of the light as it passes through the fibre?
2017 Question 11 [Higher Level]
In the late 20th century, communication of signals using optical fibres became a reality, with several cables laid across the Atlantic. In 2015 the Hibernia Express optical cable was completed. It connects Cork and London to Halifax and New York and carries a signal from London to New York in 29 milliseconds.
Read the following passage and answer the accompanying questions.
The Irish Low Frequency Array, or I‐LOFAR, is part of a €150 million network of radio telescope stations spread across seven European countries. It detects radio waves with wavelengths between 1.3 m and 30 m.
An example of a modern telescope is the Hubble telescope, which is in low Earth orbit 570 km above the ground. It undergoes 15.1 orbits per day. Hubble’s position allows it to take extremely high‐resolution images.
Adapted from rte.ie and nasa.gov
Where, with respect to the concave mirror, will an image of the moon be formed?
Justify your answer.
Lenses: Ordinary level
2019 Question 11 [Ordinary Level]
Adapted from https://science.howstuffworks.com/innovation/everyday‐innovations/lens6
Name the part of the eye where an image is formed.
 Copy the diagram below into
your answerbook and complete the ray diagram to form a real
image.
Copy the diagram below into
your answerbook and complete the ray diagram to form a real
image.The power required to clearly view a nearby object is 38 m‐1.
A person with an eye defect has a maximum power of 32 m‐1.
Calculate the power of the lens required to correct this defect?
What is the focal length of this lens?
Refraction is the bending of light as it passes from one medium into another.
State Snell’s law of refraction.
Copy and complete the diagram below to show the paths of the rays of light after they strike the converging lens.
A converging lens can be used to produce a magnified virtual image.
State one use of a lens.
2022 Question 14 (b) [Ordinary Level]
If the light from a distant object comes to focus in front of the retina, the person will see a blurred image. This person is said to be short sighted.
What type of lens is used to correct short sightedness?
Lenses: Higher level
2021 Question 14 (d) [Higher Level]
Ball lenses are glass spheres which can be used for special effects in photography.
What is meant by critical angle?
Calculate the speed of light in the ball lens.
A converging lens of focal length 20 cm and a diverging lens of focal length 8 cm are placed in contact.
Calculate the power of the combination.What eye defect can be corrected using converging lenses?
The power of a normal eye is +60 m-1. A short-sighted person’s eye has a power of +65 m-1.
Calculate the power of the contact lens required to correct the person’s short-sightedness.
A diverging lens cannot be used as a magnifying glass. Explain why.
The converging lens has a focal length of 8 cm.
Determine the two positions that an object can be placed to produce an image that is four times the size of the object?
2008 Question 9 [Higher Level]
What is meant by refraction of light?
Calculate the maximum power of the internal lens.
Light is refracted as it enters the cornea from air as shown in the diagram.
What is the maximum power of the eye?
Why do objects appear blurred?
GEOMETRICAL
OPTICS EXAM SOLUTIONS 2002 - 2022:
ORD. LEVEL MATHS PARTS ONLY
2004 Question 12 (b) [Ordinary Level]
How far from the mirror will the image be formed?
2014 Question 8 [Ordinary Level]
In the diagram the value of the angle i is 380.
An optical fibre cable has a refractive index of 1.5.
Calculate the angle at which total internal reflection occurs.
$n_{g} = \frac{1}{\sin C}$ $\sin C = \frac{1}{n_{g}}$ $\sin C = \frac{1}{1.5}$ sin C = 0.66 C = sin−10.66 C = 41.80
2020 Question 7 [Ordinary Level]
Use Snell’s law to calculate the refractive index of water.
An object of height 2 cm is placed 17 cm in front of a concave mirror.
An image with a height of 3 cm is formed
Calculate the position of the real image formed.
1/u + 1/v = 1/f
v = 30 cmThe object has a height of 4 cm. Calculate the height of the image.
m = v/u = 1.5
image height = 4 × 1.5 = 6 cm
Calculate the focal length of the lens in the glasses.
$f = \frac{1}{P}$ $f = \frac{1}{2}$= 0.5 m
GEOMETRICAL OPTICS EXAM SOLUTIONS 2002 - 2022: HIGHER LEVEL
The ratio of the sin of the angle of incidence to the sin of the angle of refraction is a constant.
Draw a labelled diagram showing the optical structure of the eye.
PTotal = P1 + P2 Pcorrected eye = Pdefective eye + Pcorrective lens
60 = 65 + P2
2004 Question 12 (b)
Give two reasons why the telecommunications industry uses optical fibres instead of copper conductors to transmit signals.
A light ray is introduced at one end of the fibre and strikes the interface at an angle greater than the critical angle so total internal reflection occurs.
This continues all along the fibre.
Calculate the speed of light travelling through the optical fibre.
$refractive\ index = \frac{speed\ of\ light\ in\ air}{speed\ of\ light\ in\ medium}$
Refraction is the bending of light as it passes from one medium to another.
Draw a ray diagram to show how an erect image is formed by a magnifying glass.
$M = \frac{v}{u}$ The image is 4 times the size of the object ⇒ M =4 $4 = \frac{v}{u}$ ⇒ v=4u
$\frac{1}{f} = \frac{1}{u} + \frac{1}{v}$ ⇒ $\frac{1}{8} = \frac{1}{u} + \frac{1}{4u}$ ⇒ $\frac{1}{8} = \frac{(4)1 + (1)1}{4u}$ ⇒ $\frac{1}{8} = \frac{5}{4u}$ ⇒ 4u = 40
⇒ u =10 cm
Calculate the focal length of the lens required to correct this defect.
PTotal = P1 + P2 ⇒ PCorrected lens = Pdefective lens + Pcorrective lens
Name the defect.
Short sight / myopia
The ratio of the sin of the angle of incidence to the sin of the angle of refraction is a constant.
Calculate how near an object can be placed in front of the eye and still be in focus.
Calculate the maximum power of the internal lens.
Ptotal = P1 + P2 PTotal = Pfixed lens + Pvariable lens 64 = 38 + P2 P2 = 26 m-1
When underwater why does the cornea not act as a lens?
Because the cornea has the same refractive index as water, therefore light doesn’t bend as it passes from water into the cornea.
Explain how wearing goggles allows objects to be seen clearly.
Because light which hits the cornea is now entering the cornea from air and therefore will refract so the cornea will once again act as a lens.
Light enters one end of the fibre and strikes the boundary between the two materials at an angle greater than the critical angle, resulting in total internal reflection at the interface.
This reflected light now strikes the interface on the opposite wall and gets totally reflected again.
$Refractive\ Index = \frac{C_{air}}{C_{glass}}$ ⇒ $C_{glass} = \frac{C_{air}}{Refractive\ Index}$ = $\frac{{3.0\ \times \ 10}^{8}}{1.55}$ = 1.94 × 108 m s-1
What is the power being transmitted by the light after it has travelled 8 km through the fibre?
State the laws of refraction of light.
The incident ray, refracted ray and normal all lie in same plane
The angle of a ray of light coming from the lamp to a point on the surface outside the disc will be greater than the critical angle so gets totally internally reflected.
Calculate the area of the illuminated disc of water.
$\tan{C = \ \frac{r}{1.8}}$ r = 1.8 tan C r = 2.053 m Area = πr2 = π(2.053 )2
Area = 13.24 m2
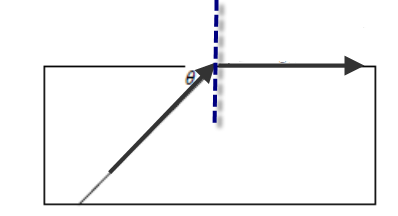
What would be the value of the angle θ so that the ray of light emerges parallel to the side of the glass block?
Calculate the speed of light as it passes through the glass.
$n_{g} = \ \frac{c_{a}}{c_{g}}$ $c_{g} = \frac{{2.9979\ \times 10}^{8}}{1.5}$ cg = 2 ×108 m s-1
{Note that the focus is half-way between the centre of curvature and the mirror. The diameter of the decoration is 20 cm. Therefore the radius is 10 cm. Therefore the centre of curvature is 10 cm from the mirror. Therefore f = 5 cm.}
Note also that we make $\frac{1}{f}$ negative to represent the fact that we are dealing with a convex mirror.
2017 Question 11
With the aid of a labelled diagram, explain how light is transmitted through optical fibres.
Speed of light in air = 3 × 108 m s-1
Speed of light in glass = $\frac{distance}{time} = \ \frac{5500\ \times \ 10^{3}}{29\ \times \ 10^{- 3}}$ = 1.9 × 108 m s-1
The opposite happens at the second interface (light ray bends away from the normal).
The opposite happens at the second interface (light ray bends away from the normal).
P1 = $\frac{1}{0.2}$ = 5 m-1 P2 = $\frac{1}{- 0.08}$ = -12.5 m-1 {the second lens is diverging and so is negative}
Ptotal = 5 – 12.5 m-1 Ptotal = –7.5 m–1
Calculate the distance from the sheet to the mirror.
Explain why this image was not of use to Rembrandt.
The image formed would be a virtual image which could not be formed on a sheet
$f = \frac{c}{\lambda}$ = $\frac{3\ \times \ 10^{8}}{30}$ f = 1 × 107 Hz
Draw a diagram of the magnetic field around the Earth.
See diagram
Calculate the position of the image of a person standing 75 cm from the Leviathan mirror.
$\frac{1}{f} = \frac{1}{u} + \frac{1}{v}$ $\frac{1}{16} = \frac{1}{0.75} + \frac{1}{v}$ $\frac{1}{16} - \frac{1}{0.75} = \frac{1}{v}$ $- \frac{61}{48} = \frac{1}{v}$
See diagram
Calculate the velocity of the Hubble telescope as it orbits the Earth.
So the radius of this circle = (6400 + 470) km = 6870 km = 6.87 × 106 m
So the distance travelled in one orbit corresponds to the circumference of this circle = 2πr
$v = \frac{distance\ }{time} = \ \frac{2\pi(6.87\ \times \ 10^{6})}{5720.4}$ = 7650 m s-1
Name one optical phenomenon . . .
How does the location of the Hubble telescope eliminate this problem?
The formula for area of a disc is πr2, so we need a value for r.
First we can calculate a value for the critical angle C using
A diver is 12 m below the surface in a pool of water.
Use a labelled diagram to explain why the diver does not appear to be at a depth of 12 m when viewed by an observer outside the pool.
correct refracted ray
correct apparent ray / correct position of image
2021 Question 14 (d)
What is meant by critical angle?
angle of incidence (in denser medium)
such that angle of refraction is 90°/ greater than which total internal reflection occursCalculate the speed of light in the ball lens.
travel at different speeds (in glass) / have different refractive indices