Squad and squad and test set results for race
Figure 1. Model (blue) and model+data (green) parallel FLOPS as a function of number of GPUs. Model parallel (blue): up to 8-way model parallel weak scaling with approximately 1 billion parameters per GPU (e.g. 2 billion for 2 GPUs and 4 billion for 4 GPUs). Model+data parallel (green): similar configuration as model parallel combined with 64-way data parallel.
a baseline by training a model of 1.2 billion parameters on a single NVIDIA V100 32GB GPU, that sustains 39 TeraFLOPs. This is 30% of the theoretical peak FLOPS for a single GPU as configured in a DGX-2H server, and is thus a strong baseline. Scaling the model to 8.3 billion parameters on 512 GPUs with 8-way model parallelism, we achieve up to 15.1 PetaFLOPs per second sustained over the entire application. This is 76% scaling efficiency compared to the single GPU case. Figure 1 shows more detailed scaling results.
• We show that careful attention to the placement of layer normalization in BERT-like models is critical to achieving increased accuracies as the model grows.
• We demonstrate that scaling the model size results in improved accuracies for both GPT-2 (studied up to 8.3 billion parameters) and BERT (studied up to 3.9B parameters) models.
Pretrained language models have become an indispensable part of NLP researchers’ toolkits. Leveraging large corpus pretraining to learn robust neural representations of lan-guage is an active area of research that has spanned the past decade. Early examples of pretraining and transferring neural representations of language demonstrated that pre-trained word embedding tables improve downstream task results compared to word embedding tables learned from scratch (Mikolov et al., 2013; Pennington et al., 2014; Turian et al., 2010). Later work advanced research in this area by learning and transferring neural models that capture contex-tual representations of words (Melamud et al., 2016; Mc-Cann et al., 2017; Peters et al., 2018; Radford et al., 2017; 2019). Recent parallel work (Ramachandran et al., 2016; Howard & Ruder, 2018; Radford et al., 2018; Devlin et al., 2018; Liu et al., 2019b; Dai et al., 2019; Yang et al., 2019; Liu et al., 2019a; Lan et al., 2019) further builds upon these ideas by not just transferring the language model to extract contextual word representations, but by also finetuning the language model in an end to end fashion on downstream tasks. Through these works, the state of the art has advanced from transferring just word embedding tables to transferring entire multi-billion parameter language models. This pro-gression of methods has necessitated the need for hardware, systems techniques, and frameworks that are able to oper-ate efficiently at scale and satisfy increasing computational needs. Our work aims to provide the tools necessary to take another step forward in this trend.
2.2. Transformer Language Models and Multi-Head Attention
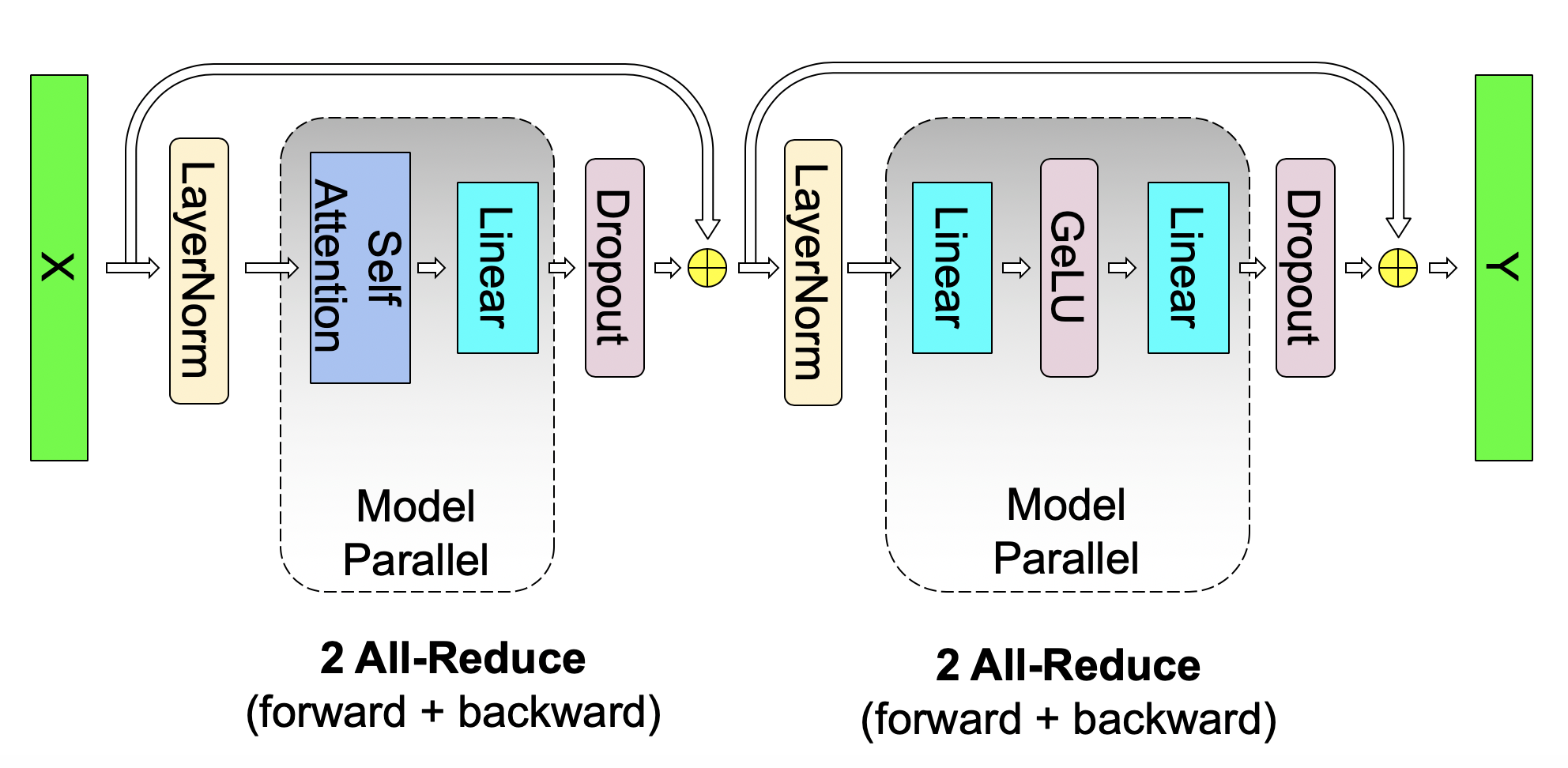
and compute efficiency. The original transformer formula-tion was designed as a machine translation architecture that transforms an input sequence into another output sequence using two parts, an Encoder and Decoder. However, recent work leveraging transformers for language modeling such as BERT (Devlin et al., 2018) and GPT-2 (Radford et al., 2019) use only the Encoder or Decoder depending on their needs. This work explores both a decoder architecture, GPT-2, and an encoder architecture, BERT.
Figure 2 shows a schematic diagram of the model we used. We refer the reader to prior work for a detailed descrip-tion of the model architecture (Vaswani et al., 2017; Devlin et al., 2018; Radford et al., 2019). It is worthwhile to men-tion that both GPT-2 and BERT use GeLU (Hendrycks & Gimpel, 2016) nonlinearities and layer normalization (Ba et al., 2016) to the input of the multi-head attention and feed forward layers, whereas the original transformer (Vaswani et al., 2017) uses ReLU nonlinearities and applies layer normalization to outputs.
Within model parallelism, there are two further paradigms: layer-wise pipeline parallelism, and more general distributed tensor computation. In pipeline model parallelism, groups of operations are performed on one device before the outputs are passed to the next device in the pipeline where a differ-ent group of operations are performed. Some approaches (Harlap et al., 2018; Chen et al., 2018) use a parameter server (Li et al., 2014) in conjunction with pipeline par-allelism. However these suffer from inconsistency issues. The GPipe framework for TensorFlow (Huang et al., 2018) overcomes this inconsistency issue by using synchronous gradient decent. This approach requires additional logic to handle the efficient pipelining of these communication and computation operations, and suffers from pipeline bubbles that reduce efficiency, or changes to the optimizer itself which impact accuracy.
Distributed tensor computation is an orthogonal and more general approach that partitions a tensor operation across multiple devices to accelerate computation or increase model size. FlexFlow (Jia et al., 2018), a deep learning framework orchestrating such parallel computation, pro-vides a method to pick the best parallelization strategy. Re-cently, Mesh-TensorFlow (Shazeer et al., 2018) introduced a language for specifying a general class of distributed ten-sor computations in TensorFlow (Abadi et al., 2015). The parallel dimensions are specified in the language by the end user and the resulting graph is compiled with proper collective primitives. We utilize similar insights to those leveraged in Mesh-TensorFlow and exploit parallelism in computing the transformer’s attention heads to parallelize our transformer model. However, rather than implementing a framework and compiler for model parallelism, we make only a few targeted modifications to existing PyTorch trans-former implementations. Our approach is simple, does not
We start by detailing the MLP block. The first part of the block is a GEMM followed by a GeLU nonlinearity:
Y = GeLU(XA) (1)
tion.
Another option is to split A along its columns A = [A1, A2]. This partitioning allows the GeLU nonlinearity to be inde-pendently applied to the output of each partitioned GEMM:
| class f(torch.autograd.Function): |
|---|
|
|---|
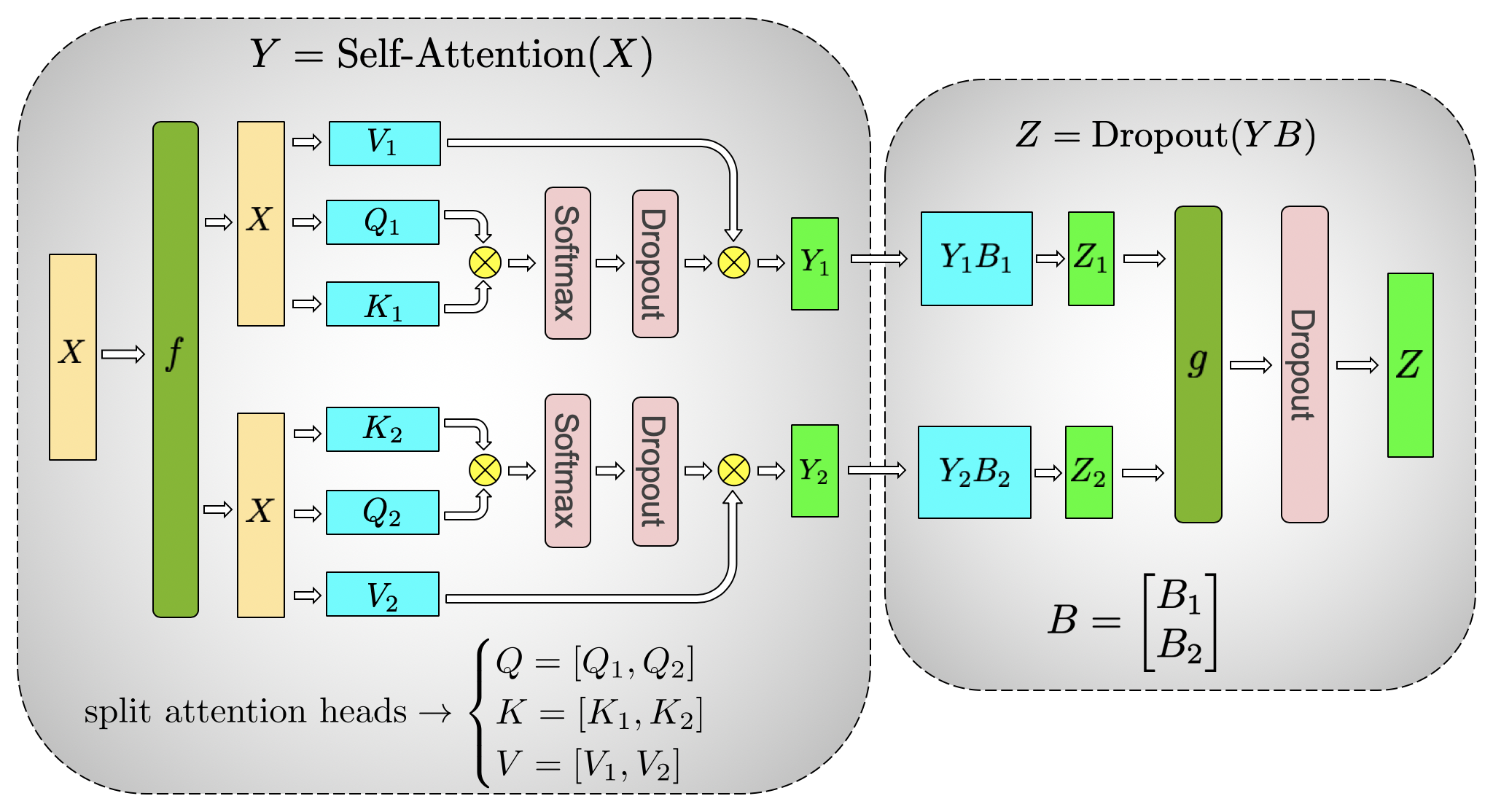
(b) Self-Attention
Figure 4. Communication operations in a transformer layer. There are 4 total communication operations in the forward and backward pass of a single model parallel transformer layer.
Pretrained language understanding models are central tasks in natural language processing and language understanding. There are several formulations of language modeling. In this work we focus on GPT-2 (Radford et al., 2019), a left-to-right generative transformer based language model, and BERT (Devlin et al., 2018), a bi-directional transformer model based on language model masking. We explain our configurations for these models in the following section and refer to the original papers for more details.
4.1. Training Dataset
|
|---|
For GPT-2 models, all training is performed with sequences of 1024 subword units at a batch size of 512 for 300k itera-
All of our experiments use up to 32 DGX-2H servers (a total of 512 Tesla V100 SXM3 32GB GPUs). Our infrastruc-ture is optimized for multi-node deep learning applications, with 300 GB/sec bandwidth between GPUs inside a server via NVSwitch and 100 GB/sec of interconnect bandwidth between servers using 8 InfiniBand adapters per server.
5.1. Scaling Analysis
| 1 | 2 | 4 | 8 | … | 64 | 128 | 256 | 512 |
|---|
done by scaling the batch-size, however, this approach does not address training large models that do not fit on a single GPU and it leads to training convergence degradation for large batch sizes. In contrast, here we use weak scaling to train larger models that were not possible otherwise. The baseline for all the scaling numbers is the first configuration (1.2 billion parameters) in Table 1 running on a single GPU. This is a strong baseline as it achieves 39 TeraFLOPS during the overall training process, which is 30% of the theoretical peak FLOPS for a single GPU in a DGX-2H server.
Figure 5 shows scaling values for both model and model+data parallelism. We observe excellent scaling num-bers in both settings. For example, the 8.3 billion parame-ters case with 8-way (8 GPU) model parallelism achieves 77% of linear scaling. Model+data parallelism requires fur-ther communication of gradients and as a result the scaling numbers drop slightly. However, even for the largest config-uration (8.3 billion parameters) running on 512 GPUs, we achieve 74% scaling relative to linear scaling of the strong single GPU baseline configuration (1.2 billion parameters).
Table 2. Model configurations used for GPT-2.
Table 3. Zero-shot results. SOTA are from (Khandelwal et al., 2019) for Wikitext103 and (Radford et al., 2019) for LAMBADA.
| Model | Wikitext103 Perplexity ↓ | LAMBADA Accuracy ↑ |
|---|---|---|
| Previous SOTA | 15.79 | 63.24% |
Figure 6 shows validation perpelixity as a function of num-ber of iterations. As the model size increases, the validation perpelixity decreases and reaches a validation perplexity of 9.27 for the 8.3B model. We report the zero-shot evaluation of the trained models on the LAMBADA and WikiText103 datasets in Table 3. For more details on evaluation method-ology, see Appendix E. We observe the trend that increasing model size also leads to lower perplexity on WikiText103 and higher cloze accuracy on LAMBADA. Our 8.3B model achieves state of the art perplexity on the WikiText103 test set at a properly adjusted perplexity of 10.81. At 66.51% accuracy, the 8.3B model similarly surpasses prior cloze accuracy results on the LAMBADA task. We have included samples generated from the 8.3 billion parameters model in the Appendix C. Recently researchers from Microsoft in collaboration with NVIDIA trained a 17 billion parameter GPT-2 model called Turing-NLG (Microsoft, 2020) using Megatron and showed that the accuracies further improve as they scale the model, highlighting the value of larger models.
To ensure we do not train on any data found in our test sets, we calculate the percentage of test set 8-grams that also appear in our training set as done in previous work (Rad-ford et al., 2019). The WikiText103 test set has at most
In this section, we apply our methodology to BERT-style transformer models and study the effect of model scaling on several downstream tasks. Prior work (Lan et al., 2019) found that increasing model size beyond BERT-large with 336M parameters results in unexpected model degradation. To address this degradation, the authors of that work (Lan et al., 2019) introduced parameter sharing and showed that that their models scale much better compared to the original BERT model.
We further investigated this behaviour and empirically demonstrated that rearranging the order of the layer nor-malization and the residual connections as shown in Figure 7 is critical to enable the scaling of the BERT-style mod-els beyond BERT-Large. The architecture (b) in Figure 7 eliminates instabilities observed using the original BERT architecture in (a) and also has a lower training loss. To the best of our knowledge, we are the first to report such a change enables training larger BERT models.
| Model | trained tokens ratio | MNLI m/mm accuracy (dev set) |
QQP accuracy (dev set) |
SQuAD 1.1 F1 / EM (dev set) |
SQuAD 2.0 F1 / EM (dev set) |
|
|---|---|---|---|---|---|---|
| RoBERTa (Liu et al., 2019b) ALBERT (Lan et al., 2019) XLNet (Yang et
al., 2019) Megatron-336M Megatron-1.3B Megatron-3.9B |
|
|
||||
|
89.4 (91.2 / 88.6) 90.9 (93.1 / 90.0) | |||||
Using the architecture change in Figure 7(b), we consider three different cases as detailed in Table 4. The 336M model has the same size as BERT-large. The 1.3B is the same as the BERT-xlarge configuration that was previously shown to get worse results than the 336M BERT-large model (Lan et al., 2019). We further scale the BERT model using both larger hidden size as well as more layers to arrive at the 3.9B parameter case. In all cases, the hidden size per attention head is kept constant at 64. 336M and 1.3B models are trained for 2 million iterations while the 3.9B model is trained for 1.5 million iterations and is still training.
On a 3% held-out set, 336M, 1.3B, and 3.9B models achieve validation set perplexity of 1.58, 1.30, and 1.16, respectively, a monotonic decrease with the model size. We finetune the trained models on several downstream tasks including MNLI and QQP from the GLUE benchmark (Wang et al., 2019), SQuAD 1.1 and SQuAD 2.0 from the Stanford Ques-tion answering dataset (Rajpurkar et al., 2016; 2018), and the reading comprehension RACE dataset (Lai et al., 2017). For finetuning, we follow the same procedure as (Liu et al., 2019b). We first perform hyperparameter tuning on batch
Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism
investigation that will further test existing deep learning hardware and software. To realize this, improvements in the efficiency and memory footprint of optimizers will be needed. In addition, training a model with more than 16 billion parameters will demand more memory than is avail-able within 16 GPUs of a DGX-2H box. For such models, a hybrid intra-layer and inter-layer model parallelism along with inter-node model parallelism would be more suitable. Three other directions of investigation include (a) pretrain-ing different model families (XLNet, T5), (b) evaluating per-formance of large models across more difficult and diverse downstream tasks (e.g. Generative Question Answering, Summarization, and Conversation), and (c) using knowl-edge distillation to train small student models from these large pretrained teacher models.
Chen, T., Xu, B., Zhang, C., and Guestrin, C. Train- ing deep nets with sublinear memory cost. CoRR, abs/1604.06174, 2016. URL .
Dai, Z., Yang, Z., Yang, Y., Carbonell, J. G., Le, Q. V., and Salakhutdinov, R. Transformer-xl: Attentive lan- guage models beyond a fixed-length context. CoRR, abs/1901.02860, 2019. URL .
Hendrycks, D. and Gimpel, K. Bridging nonlinearities and stochastic regularizers with gaussian error linear units. CoRR, abs/1606.08415, 2016. URL .
Howard, J. and Ruder, S. Fine-tuned language models for text classification. CoRR, abs/1801.06146, 2018.
Khandelwal, U., Levy, O., Jurafsky, D., Zettlemoyer, L., and Lewis, M. Generalization through memorization: Nearest neighbor language models. arXiv:1911.00172, 2019.
Kingma, D. P. and Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism
Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D., Levy, O., Lewis, M., Zettlemoyer, L., and Stoyanov, V. Roberta: A robustly optimized BERT pretraining approach. CoRR, abs/1907.11692, 2019b. URL .
URL .
Micikevicius, P., Narang, S., Alben, J., Diamos, G. F., Elsen, E., Garcia, D., Ginsburg, B., Houston, M., Kuchaiev, O., Venkatesh, G., and Wu, H. Mixed precision training. CoRR, abs/1710.03740, 2017.
NVIDIA. Mixed precision training: Choosing a scaling factor, 2018. URL
.
Radford, A., J´ozefowicz, R., and Sutskever, I. Learning to generate reviews and discovering sentiment. CoRR, abs/1704.01444, 2017.
Radford, A., Narasimhan, K., Salimans, T., and Sutskever, I. Improving language understanding by generative pre-training, 2018. URL
Ramachandran, P., Liu, P. J., and Le, Q. V. Unsupervised pretraining for sequence to sequence learning. CoRR, abs/1611.02683, 2016. URL .
Shazeer, N., Cheng, Y., Parmar, N., Tran, D., Vaswani, A., Koanantakool, P., Hawkins, P., Lee, H., Hong, M., Young, C., Sepassi, R., and Hechtman, B. Mesh-TensorFlow: Deep learning for supercomputers. In Neural Information Processing Systems, 2018.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., and Polosukhin, I. Attention is all you need. CoRR, abs/1706.03762, 2017.
Wang, A., Singh, A., Michael, J., Hill, F., Levy, O., and Bowman, S. R. Glue: A multi-task benchmark and analy-sis platform for natural language understanding. ICLR, 2019.
Zhu, Y., Kiros, R., Zemel, R. S., Salakhutdinov, R., Urta-sun, R., Torralba, A., and Fidler, S. Aligning books and movies: Towards story-like visual explanations by watch-ing movies and reading books. CoRR, abs/1506.06724, 2015.
A. BERT Finetuning Hyperparameters
Model parallelism is orthogonal to data parallelism, and so we can use both simultaneously to train large models in a reasonable amount of time. Figure 8 shows a grouping of GPUs for hybrid model and data parallelism. Two or more GPUs within the same server form model parallel groups (for example GPUs 1 to 8 in Figure 8), and contain one
Table 6. Hyperparameters for finetuning BERT model on down-stream tasks.
| MNLI | 336M 1.3B 3.8B |
128 | 1e-5 | 10 |
| QQP | 336M 1.3B 3.8B |
12 | ||
| SQUAD 1.1 | 336M 1.3B 3.8B |
|
|
2 |
| SQUAD 2.0 | 336M 1.3B 3.8B |
2 | ||
| RACE | 336M 1.3B 3.8B |
3 | ||
instance of the model distributed across these GPUs. The remaining GPUs, which could be within the same server but more typically are located in other servers, run additional model parallel groups. GPUs with the same position in each of the model parallel groups (for example GPUs 1, 9, ..., 505 in Figure 8) form data parallel groups so that all GPUs within a data parallel group hold the same model param-eters. During back propagation we run multiple gradient all-reduce operations in parallel to reduce weight gradients within each distinct data parallel group. The total number of required GPUs is the product of the number of model and data parallel groups. For example, for the 8.3 billion parameter model we use 8 GPUs per model parallel group and 64-way data parallelism, for a total of 512 GPUs. All communication is implemented in PyTorch by Python calls to NCCL. GPUs within each model parallel group perform all-reduces amongst all GPUs within the group. For data parallelism, each of the all-reduce operations takes place with one of the GPUs from each model parallel group.
B.2. Model Parallel Random Number Generation
Figure 8. Grouping of GPUs for hybrid model and data parallelism with 8-way model parallel and 64-way data parallel.
C. Text Samples
|
|---|
|
|---|
|
|---|
D.2. Strong Scaling
Our model parallelism is primarily designed to enable train-ing models larger than what can fit in the memory of a
Table 8. Speedup obtained for the 1.2 billion parameters model using model parallelism while keeping the batch size constant.
| # of GPUs | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| Speedup | 1.0 | 1.64 | 2.34 | 2.98 |
WikiText103 perplexity is an evaluation criterion that has been well studied over the past few years since the creation of the benchmark dataset. Perplexity is the exponentiation of the average cross entropy of a corpus (Mikolov et al., 2011). This makes it a natural evaluation metric for lan-guage models which represent a probability distribution over entire sentences or texts.
E.2. LAMBADA Cloze Accuracy
The capability to handle long term contexts is crucial for state of the art language models and is a necessary prerequi-site for problems like long-form generation and document-based question answering. Cloze-style datasets like LAM-BADA are designed to measure a model’s ability to operate in and reason about these types of long term contexts. Cloze-style reading comprehension uses a context of word tokens x = x1:t with one token xj masked; the models objective is to correctly predict the value of the missing jthtoken. To accurately predict the missing token, the model requires an in-depth understanding of the surrounding context and how language should be used in such a context. LAMBADA uses cloze-style reading comprehension to test generative left-to-right language models by constructing examples of 4-5 sentences where the last word in the context xt is masked. Our models utilize subword units, so for LAMBADA evalu-ation we utilize the raw, unprocessed LAMBADA dataset and require that our model predict the multiple subword tokens that make up the word token. We use teacher forc-ing, and consider an answer correct only when all output predictions are correct. This formulation is equivalent to the original task of word token prediction.