Then applying the power logarithmic rule
A ={x : x ∈ Z and x2 < 100}
[2]
ii. Rewrite the following set using the set builder method:
Firstly, a Venn diagram of A∩B followed by a Venn diagram of A * B:
Since A * B = A∩B = U - A∩B, thus the Venn diagram for A * B will be:
ii. By using the laws of the algebra of sets show that the following is true:
(A * A) * (B * B) = (A∩A) ∩ (B∩B)
A ∪ B Idempotent Identity
• (A * B) * (A * B) = A∩B [2]
(A∩B ∪ A) ∩ (A∩B ∪ B) Distributive Identity
A ∩ (B∪A ∩ B∪B) Distributive Identity
A ∩ B Absorption
that (A ∪ B∪ C) ∩ (A ∪ B ∪ C) ∩ (A∪C) = Ø [4]
(A∩C) ∩ (A ∪ B∪ C) ∩ (A ∪ B ∪ C) De Morgan’s Law
(Ø∩C) ∪ (A∩C∩B) ∪ (A∩Ø) ∩ (A ∪ B ∪ C) Complement Law
(A∩C∩B∩A) ∪ (A∩C∩B∩B) ∪ (A∩C∩B∩C) Distributivity
(Ø) ∪ (Ø) ∪ (Ø) Identity Law
Thus, (A ∪ B∪ C) ∩ (A ∪ B ∪ C) ∩ (A∪C) = Ø
(a) Let f (x) = x mod 3, where f (x) is the remainder when x is divided by 3,
f(7) = 7 mod 3 = 1
f(12) = 12 mod 3 = 0
iii. Say whether or not f(x) is injective( one-to-one), justifying your answer. [2]
f is said to be injective or one-to-one function, if and only if any two different inputs will lead to two different outputs. Such that:
A counter example showing that f(a) = f(b) but a ≠ b.
iv. Say whether or not f(x) is surjective(onto), justifying your answer. [2]
f is set to be a surjective or an onto function if and only if every element of the co-domain of f, {0, 1, 2}, has at least one pre-image in the domain of f, N. This means that given any element y of {0, 1, 2}, there exists an element x of N such that y is the image of x. Hence, the co-domain of f must be equal to the range of f. Such that:
co-Df = {0, 1, 2} and Rf = {0, 1, 2}
A function is said to be bijective and invertible, if and only if it is both injective and surjective.
for all a, b ∈ B, if a ≠ b then g(a) ≠ g(b) ≡ for all a, b ∈ B, if g(a) = g(b) then a = b
≠ →→ ≠ →→ $$\frac{a}{a - 1}$$≠
Proof that g is surjective:
→→→→ →→$${x = \frac{y}{y - 1}}\in B$$
Since, co-Dg = Rg, thus g is surjective.
Since g was proven to be both injective and surjective, thus the function g is a bijection and invertible.
Since g was proven to be both surjective and injective, thus it is bijective and an inverse function g-1 exists and can be found.
g: B → B is defined by g(x) =$$\frac{x}{x - 1}$$
Let g(x) =$$\frac{x}{x - 1}$$= y →→$$\frac{x}{x - 1}$$= y
→→→→ $$x = \frac{y}{y - 1}$$
-Interchanging the variables x and y of g:$$x = \frac{y}{y - 1}$$
-solving for y:
-Subtracting y from both sides: →→
Therefore, g-1(x) =$$\frac{x}{x - 1}$$
→→ →→ →→ →→
→→ →→ x→→ Thus, (g օ g-1)(x) =
(c) Let f : R → ]1,+∞[ with f(x)=2x +1.
Obtaining The inverse function f-1:
- Solving for y:
- Applying the power logarithmic rule, “loga xp = p.loga x”:
Since the function f maps R to ]1, +∞[, then the inverse function f-1, maps ]1, +∞[ to R.
f-1(x) =$$\frac{\ln{({x - 1})}}{\ln{(2)}}$$ f(x) = 2x +1 (f-1 օ f)(x) =
(f-1 օ f)(x) was shown to equal x. Thus, f-1(x) =is proven to be the inverse function of f(x) = 2x +1
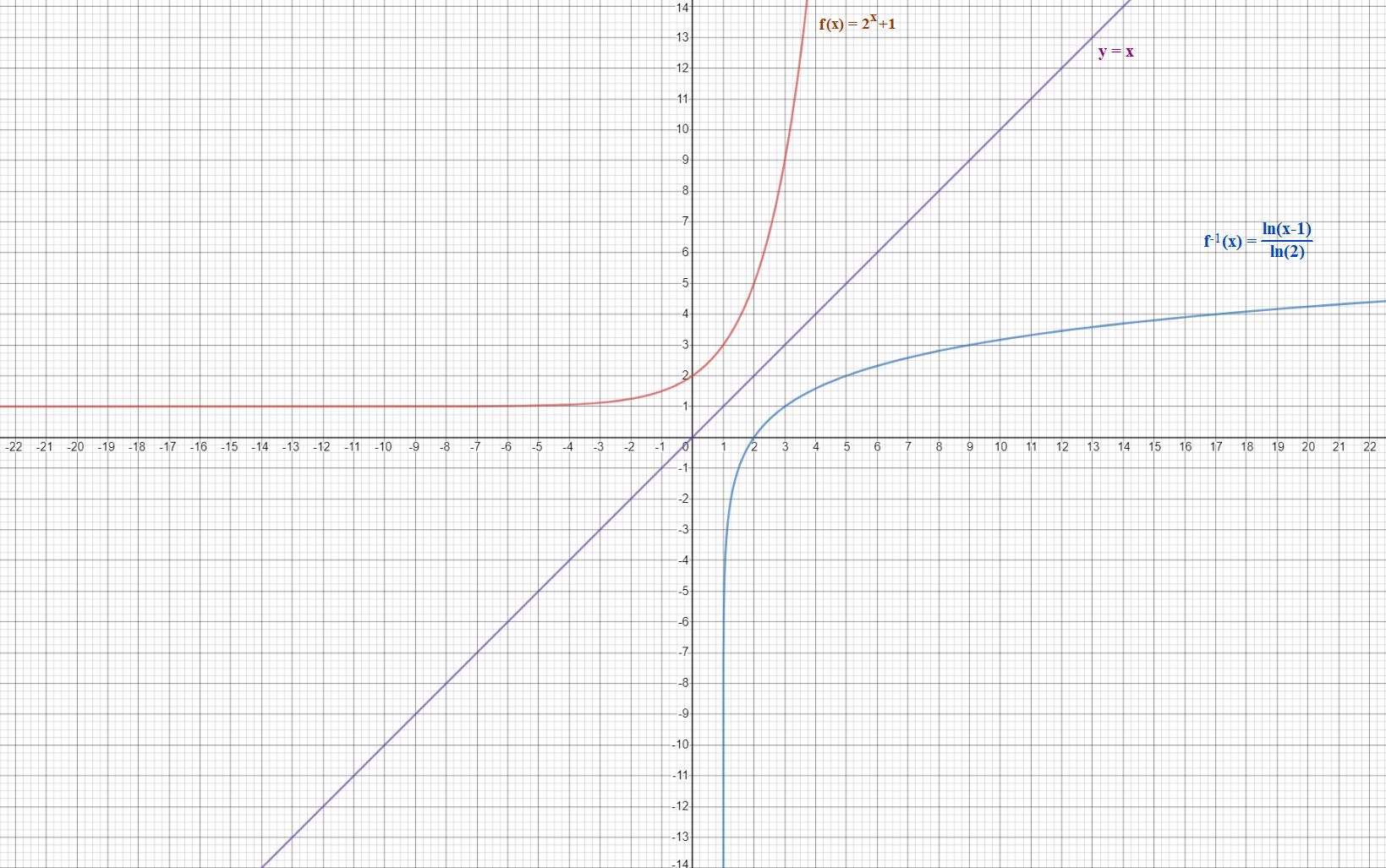
-The domain of f(x) = (-∞, +∞), and the range of f(x) = (1, +∞).
-The y-intercept of f(x): (0, 2).
-Graph of f-1 (x) shows an increasing function.
(d) Let A and B be two finite sets with |A| = |B| and f be a function from A to B. show that if f is an injective (one-to-one) function then it is also a surjective function. [4]
Question 3 Propositional Logic
| The truth table of the proposition p⊕¬q | |||
| p | q | ¬q | p⊕¬q |
| F | F | T | T |
| F | T | F | F |
| T | F | T | F |
| T | T | F | T |
¬q = U − q ¬q = {1, 2, 3, 4}
The truth set of ¬(p→ q):
∴ ¬(p→ q) = {2, 4}
(b) Let p and q be two propositions defined as follows:
‘The home football team wins whenever it’s raining’ q → p
‘neither the home football team wins nor it’s raining’ ¬p∧¬q
[4]
The implication in question is: p→q
Wording: “if it’s not raining, then the home football team does not win”
Wording: “if it’s raining, then the home football team wins”
Wording: “if the home football team does not win, then it’s not raining”
s means ’”Samir comes to the party”
c means ’”Callum comes to the party”
[4]
- i: (s∧¬c)→ j
- ii: (j→¬c) → s∧r
A way of showing that a compound proposition is a tautology, is to construct its truth table:
| The truth table of the compound proposition (p∨q)∧(¬p∨r) → (q∨r) | ||||||||
| p | q | r | (p∨q) | ¬p | (¬p∨r) | (p∨q)∧(¬p∨r) | (q∨r) | (p∨q)∧(¬p∨r) → (q∨r) |
| F | F | F | F | T | T | F | F | T |
| F | F | T | F | T | T | F | T | T |
| F | T | F | T | T | T | T | T | T |
| F | T | T | T | T | T | T | T | T |
| T | F | F | T | F | F | F | F | T |
| T | F | T | T | F | T | T | T | T |
| T | T | F | T | F | F | F | T | T |
| T | T | T | T | F | T | T | T | T |
P : If someone is a student of Discrete Mathematics, then, they must study Boolean Algebra”.
>>Must properly specify universe of discourse and that x is an element of said UoD.
Where x denotes an element in the universe of discourse S.
R can be expressed as: ∀x(B(x) ∧ A(x)) → ∃x¬A(x)
H1: P ^ Q ,
>>> Probably All Answers Are wrong
The following proof of R, using inference rules with quantifiers is supposed to prove the proposition R, but it is also wrong. Identify the erroneous step or steps in this reasoning and explain why it is wrong :
Step2 : By Existential instantiation from Step1, we get: P(c)
Step3 : By Simplification from H, we get : ∃xQ(x)
There are two errors. Both occur in step 5.
Question 5 Boolean Algebra
P : (a + b) + c = a +(b + c) Associativity Theorem
(b) Build the truth table of the Boolean function F(x,y,z) that equals 1 if and only if x.y.z = 0 [2]
| x | y | z | x.y | x.y.z | F(x, y, z) = (x.y.z) |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
- To allow more circuits to be fitted on the same chip.
- To Reduce the global cost of circuits, by reducing the number of logic gates used
ii. To produce a sum-of-product algebraic simplification, we usually use theorems. Give three examples of theorems we can use. [3]
- Identity law.
- Absorption law.
- Commutative and Distributive and Associative Laws.
- idempotent and complement laws.
- De Morgan’s laws and involution.
iii. Fill in the following K-map for the Boolean function
iv. Use the previous K-map and find a minimisation, as the sum of three terms, of the expression
F(x, y, z) = xyz + xyz + xy.z + x.y.z + xyz + x.y.z [3]
F(x, y, z) = x y + y z + x z
