Then will not fail mathematics not use online social networking site

LECTURE 24

Logical Implication, Rules of Inference,
and Proving the Validity of Arguments

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	1

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	2

Example

“Toby is a cyclist or a runner. If Toby is a cyclist, then Toby lives in Perth. Toby does not live in Perth. Therefore he is a runner.”

I Propositional calculus is perfect for this study because an argument is really just a sequence of propositions.

I All but the last proposition are considered to be true, and the last proposition is claimed to be true, by deduction.

Chapter 7: Propositional Logic		4

So just like logical equivalence, we can express logical implication in terms of a tautology.

P ∆ Q means P æ Q is a tautology

Chapter 7: Propositional Logic		5

Logical Inferences
Usual form:
(H1 · H2 · · · · · Hn) ∆ C This is traditionally written in the form:

H1
H2
...

I The proposition C is called the conclusion.

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	5

Otherwise the inference is said to be invalid or a fallacy.

I We use logical inference not just in mathematics, but in any discipline in which logical reasoning is used.

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	6

The argument can be written as:

Therefore	Toby is a cyclist or Toby is a runner.

Chapter 7: Propositional Logic		8

[(c ‚ r) · (c æ p) · ¬p] æ r.

From the truth table (see VOHP working), we find that it is a tautology.

I It is important in any field of knowledge to be able to separate the underlying logical structure of an argument from the actual context, because often context makes the analysis harder rather than easier.

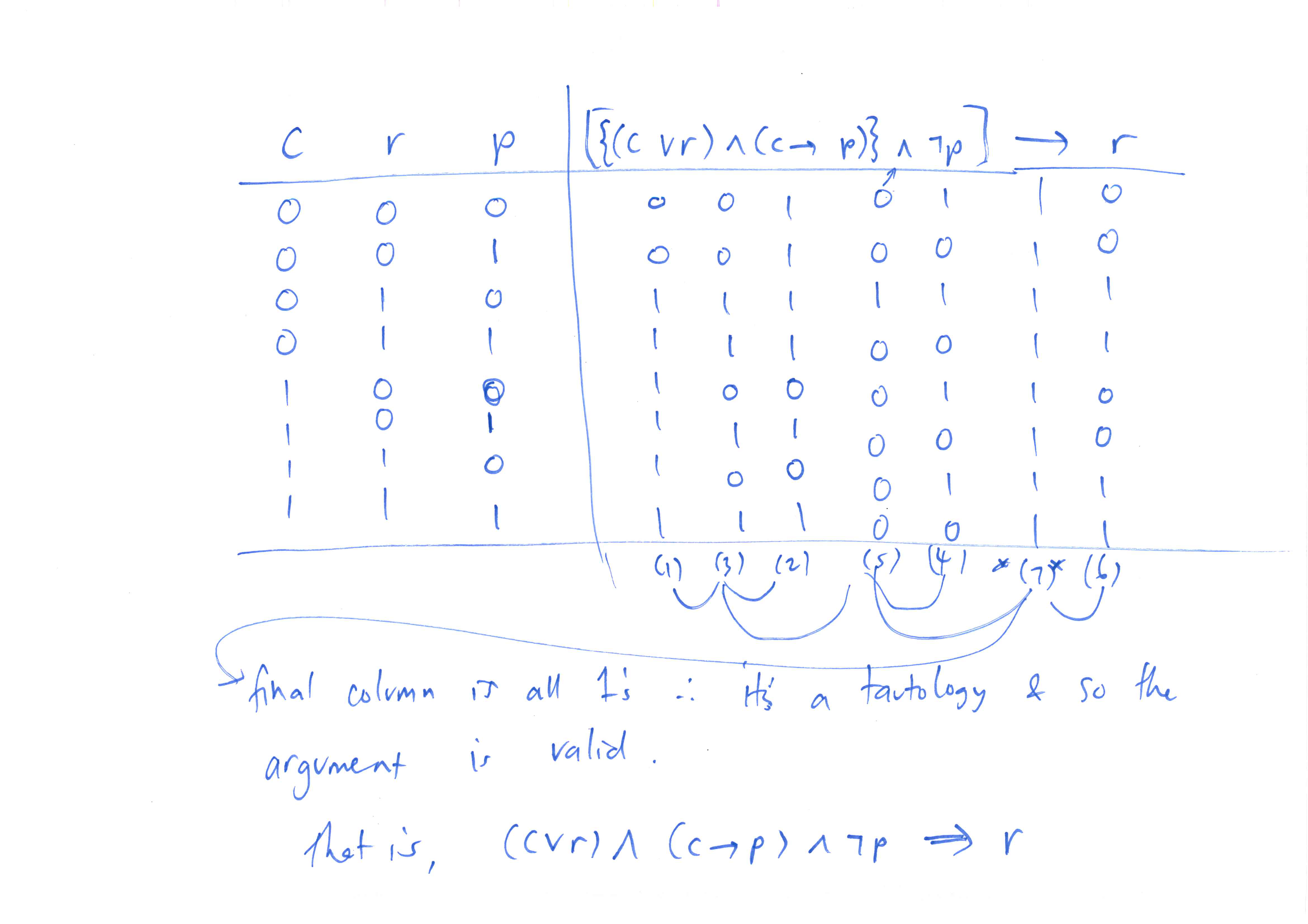
Chapter 7: Propositional Logic		9

Chapter 7: Propositional Logic	Logical Implication	10

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	10

Therefore,	If today is Sunday, then I’ll go cycling. if today is Saturday or Sunday, then I’ll go cycling.

To decide whether or not the inference is valid, we examine the truth table of the corresponding conditional:

prop(1) = p(1) <= p(3);		% Hypothesis 1
prop(2) = p(2) <= p(3);		% Hypothesis 2


prop(5) = prop(3) <= prop(4);			% Inference H1 & H2 -> C

	888	1 1 1 1 1

	888	1 0 0 0 1

	888	0 1 0 0 1

	888	0 0 0 0 1

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics			Lecture 24	12

Since the final column of the truth table, which corresponds to the

conditional:

H1 := p æ r and H2 := q æ r.

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	13

Therefore

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	14

Famous Example . . .

The conclusion is true because of the meanings of the words“Socrates” and “man”, not by inference.

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	15

Chapter 7: Propositional Logic	Rules of Inference	17

Another Famous Example

Argument in symbolic form:

	p æ q p
)

Chapter 7: Propositional Logic		18

Write the following argument in symbolic form and prove that it is logically valid.

If I study, then I will not fail mathematics.

Chapter 7: Propositional Logic		19

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	19

I It will be far more beneficial to you if you try to master the rules of inference.

I And as always, practice makes perfect!

Dr Amy Glen (Murdoch University)	MAS162 – Foundations of Discrete Mathematics	Lecture 24	20