They strike the surface the liquid and condensed

LECTURE NOTES

Subject: Chemistry-III (Basic Physical-I)

Dilute Solutions: Vapour Pressure, Raoult’s Law, and Thermodynamic Derivation of Laws Relating to Elevation of Boiling Point, Depression of Freezing Point and Osmotic Pressure. Ideal and Non-ideal Solution Association and Dissociation.

Module-II: (10 Hours)

Thermodynamic Concept: Heat Content and Heat Capacity Isothermal and Adiabaic Change, Work Done for Ideal and van der Waal Gases.

Thermochemistry: Heat Changes in Chemical Reactions, Hess’s Law, Kirchoff’s Equation. 2nd law of Thermodynamics: Spontaneous Process, Carnot’s Theorem and Carnot’s Cycle, Efficiency of Heat Engine, Entropy Changes in Reversible and Irreversible Processes, Free Energy and Work Function Condition for Equilibrium, Clapeyron and Clausius Equation, Gibb’s Helmholtz Equation.

Referred Books:
1.G.N. Barrow, Physical Chemistry, 5th Edition, Tata McGraw-Hill, 2007.

2.K.L. Kapoor, A Textbook of Physical Chemistry, 2nd Edition, Macmillan, 2011.

DISCLAIMER

The copyright is not reserved by the writer. The writer is not responsible for any legal issues arising out of any copyright demands and/or reprint issues contained in this material. This is not meant for any commercial purpose. This is solely meant for personal reference of students following the syllabus prescribed by the university. This document does not claim any originality and cannot be used as a substitute for prescribed textbooks. The information presented here is merely a collection for respective teaching assignments.

RAOULT’S LAW:

In 1986, a French Chemist named Francois Marte Raoult proposed a quantitative relation between partial pressure and mole fraction of volatile liquids. The law states that mole fraction of the solute component is directly proportional to its partial pressure.

•Non-ideal Solutions

Ideal and Non – Ideal Solutions

	It should obey Raoult’s law i.e., PA = XA and PB = XB
		Hmixing = 0, i.e. no heat should be absorbed or evolved during mixing

• • •	Ethyl chloride and ethyl bromide n–hexane and n–heptane CCl4 and SiCl4

	PA			XAP0A, PB ¹ XBP0B i.e, they do not obey Raoult’s law
		Hmixing				0,

between cyclohexane and ethanol is reduced and hence show higher vapour pressure.

Case 2:

	Acetone + Aniline Chloroform + Diethyl ether Chloroform + Benzene Water + HCl

	A-B attractive force should be weaker than A-A and B-B attractive force. “A” and “B” have different shape, size and character.

•	A-B attractive force should be greater than A-A and B-B attractive force. “A” and “B” have different shape, size and character.

Ideal solutions	Non-ideal solutions
Ideal solutions	Positive deviation from Raoult’s law	Negative deviation from Raoult’s law

	Hmix>0. Endothermic dissolution; heat is absorbed.	Hmix<0. Exothermic

	increased after dissolution.	Vmix <0. Volume is decreased during dissolution.

	A—B attractive force should be weaker than A—A and B—B attractive forces. ‘A’ and ‘B’ have different shape, size and character.	A—B attractive force should be greater than A—A and B—B attractive forces. ‘A’ and ‘B’ have different shape, size and character.

Azeotropes are defined as a mixture of two liquids which has a constant composition in liquid and vapour phase at all temperatures. Azeotropes can’t be separated by fractional distillation, as the composition of vapour phase remains same after boiling. Because of uniform composition azeotropes are also known as Constant Boiling Mixtures.

There are two types of Azeotropes:

Maximum Boiling Azeotrope is formed when we mix two non-ideal solutions at some specific composition, showing large negative deviation from Raoult’s law.

Examples:

•

boiling temperature of 373 K

Minimum Boiling Azeotrope

temperature of 351.5 K

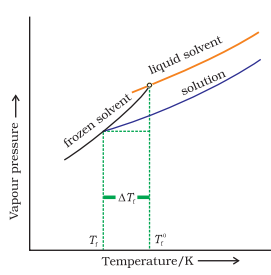
COLLIGATIVE PROPERTIES:
A dilute solution is one in which the amount of the solute is very small in comparison to the amount of the solvent.The dilute solutions show more or less ideal behavior as the heat and volume changes, accompanying the mixing of solute and solvent, are negligible for all practical purposes. Dilute solutions obey Raoult’s law. The properties of dilute solutions which depend only on number particles of solute present in the solution and not on their identity are calledcolligative properties (denoting depending upon collection).

•Depression of freezing point
•Lowering of vapour pressure
•Osmotic pressure
•Elevation of boiling point

LOWERING OF VAPOUR PRESSURE BY NON VOLATILE SOLUTE:

where P10 is the vapour pressure of the pure solvent. Since X1 + X 2 = 1, Eq. 1 may be written as

It is evident from Equation (4) that the lowering of vapour pressure of a solution depends upon the number of moles (and hence on the number of molecules) of the solute and not upon the nature of the solute dissolved in a given amount of the solvent. Hence, lowering of vapour

pressure is a colligative property.

• •

Question
The density of a 0.438 M solution of potassium chromate at 298 K is 1.063 g cm-3. Calculate the vapour pressure of water above this solution. Given : P0 (water) = 23.79 mm Hg.

Solution
A solution of 0.438 M means 0.438 mol of K2CrO4 is present in 1L of the solution. Now, Mass of K2CrO4 dissolved per litre of the solution = 0.438 194 = 84.972 g
Mass of 1L of solution = 1000 1.063 = 1063 g
Amount of water in 1L of solution = 978.028/18 = 54.255 mol
Assuming K2CrO4 to be completely dissociated in the solution, we will have; Amount of total solute species in the solution = 3 0.438 = 1.314 mol.

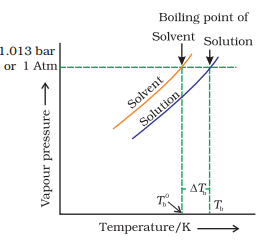
BOILING POINT ELEVATION BY A NON-VOLATILE SOLUTE:
The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to 760 mm (i.e. 1 atmospheric pressure). Since the addition of a non-volatile solute lowers the vapour pressure of the solvent, the vapour pressure of a solution is always lower than that of the pure solvent, and hence it must be heated to a higher temperature to make its vapour pressure equal to atmospheric pressure. Thus the solution boils at a higher temperature than the pure solvent. If Tb0 is the boiling point of the solvent and Tb is the boiling point of the solution, the difference in boiling points ( Tb) is called the elevation of boiling point.

		Thus, Tb –Tb0 = Tb.
		Thus, Tb –Tb0 = Tb.

Tb = Kb m

kb : molal elevation constant or Ebullioscopic constant
11

or

that, is freezing point depression of a dilute solution is directly proportional to the number of moles of the solute dissolved in a given amount of the solvent and is independent of the nature of

point of the pure solvent (Tf0). Thus, Tf0 - Tf = Tf It can be seen that

where m1 = molecular weight of solute and w and W are weights of solute and solvent.

Van't Hoff equation for dilute solutions is (parallel to ideal gas equation)

Procedure:

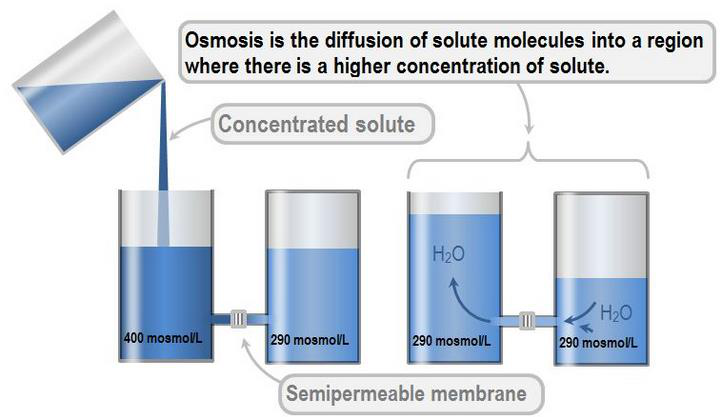
The porcelain tube is filled with pure solvent and the metallic jacket with solution. The level in the capillary tube will tend to move down as the solvent flows towards solution due to osmosis. External pressure is now applied on the solution by the piston so that level in capillary remain stationary. The reading of pressure gauge is recorded. This is the osmotic pressure of the solution.

	It is a quick and accurate method. The concentration of the solution does not change because flow of solvent is not permitted

Comparison of osmotic pressures:

Let an aqueous dilute solution filled in a capillary tube is closed at one end by semipermeable membrane. The tube is placed in pure solvent (water). Entire apparatus is closed by a belljar.