Trobe universityillustrations and web design catherine tan
Coordinate geometry
Coordinate geometry – A guide for teachers (Years 11–12)
Full bibliographic details are available from Education Services Australia.
Published by Education Services Australia
PO Box 177
Carlton South Vic 3053
Australia
Australian Mathematical Sciences Institute
Building 161
The University of Melbourne
VIC 3010
Email: enquiries@amsi.org.au
Website: www.amsi.org.au
Links forward . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 Three-dimensional coordinate geometry . . . . . . . . . . . . . . . . . . . . . . . . 29 Quadratic equations and the conics . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
History and applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
• Familiarity with the coordinate plane.
• Facility with algebra — see the module Algebra review.
Readers not familiar with coordinate geometry may find the TIMES module Introduction to coordinate geometry (Years 9–10) useful as a gentle introduction to some of the ideas in this module.
Content
intersect at a point called the origin. Once a unit distance has been chosen, the position of any point in the plane can be uniquely represented by an ordered pair of numbers (x, y). For the point (5,3), for example, 5 is the x-coordinate and 3 is the y-coordinate, sometimes called the first and second coordinates. When developing trigonometry, the four quadrants are usually called the first, second, third and fourth quadrants as shown in the following diagram.
y
| 2nd Quadrant | 1 | 5 | 6 |
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| –2 | –1 | 0 | 1 | 2 | 3 | ||||
| 3rd Quadrant |
|
||||||||
y
A(a,b)
• What is the gradient of the interval joining the two points?
• What is the equation of the line joining the two points?
• What is the equation of the perpendicular bisector of AB?
• At what angle does the line AB meet the x-axis?
y
| A |
|
|---|
AB2= |b −d|2+|a −c|2
= (a −c)2+(b −d)2.So
The distance formula
Suppose P(x1, y1) and Q(x2, y2) are two points in the number plane. Then
| PQ = |
|---|
Q(x2,y2)
P(x1,y1)
| –2 | –1 | 0 | 1 |
|
|---|---|---|---|---|
|
On the other hand, in the following diagrams, we can say that the point P divides the interval AB in the ratio 1 : 1 and the point Q divides the interval AB in the ratio 3 : 2.
B(x2,y2)
P
| A(x1,y1) | X |
|
|---|
Internal division of an interval
We now generalise the idea of a midpoint to that of a point that divides the interval AB in the ratio k : 1.
| 𝑘 | 1 | ||
|---|---|---|---|
| P |
A
Note. As k → 0, P → A and as k → ∞, P → B.
Proof
If x1 = x2, then it is clear that x is given by the formula above. So we can assume that x1 ̸= x2. Consider the points C(x, y1) and D(x2, y1), as shown in the following diagram.
| P(x,y) | 1 |
|---|
AB= AC
| k +1= x − x1 x2 − x1 |
|---|
kx2 −kx1 = kx −kx1 + x − x1
(k +1)x = kx2 + x1
x =x1+kx2 1+k .
| y =y1 |
|---|
|
|---|
We say that C divides AB externally in the ratio 2 : 1 and that D divides AB externally in the ratio 1 : 2. Clearly this is different from the internal division of an interval discussed in the previous subsection.
| 𝑘 | 1 | |
Then
x − x1 k =x − x2
AP
PB= −k.With this convention we have
|
|---|
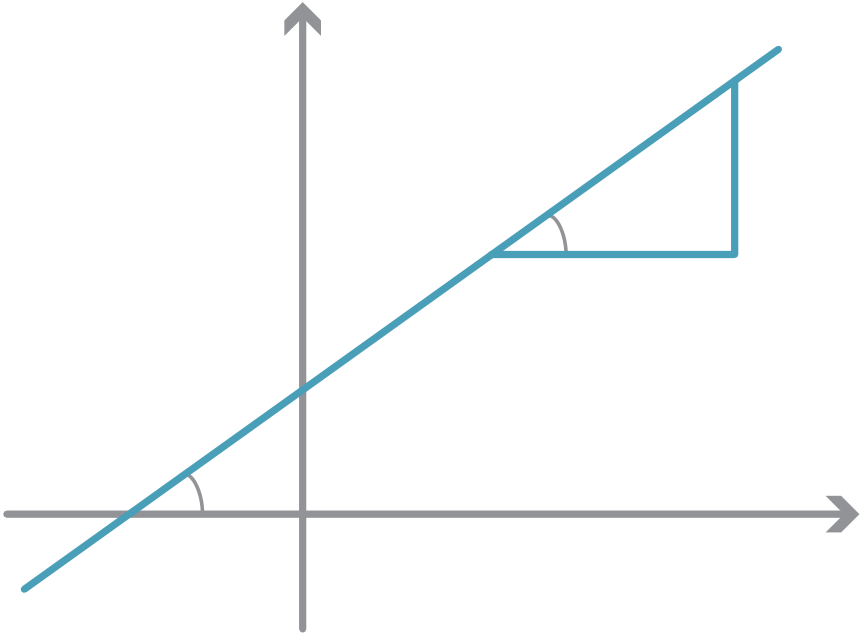
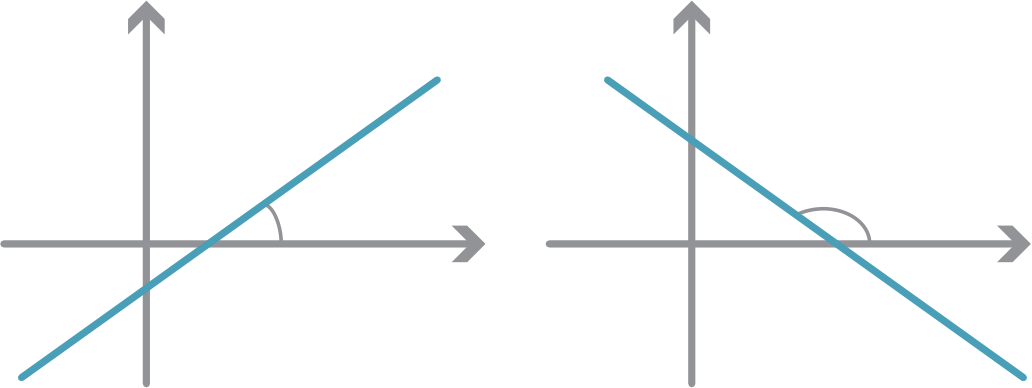
Let θ be the angle between l and the positive x-axis, where 0◦< θ < 90◦or 90◦< θ < 180◦.
Thus the gradient of any interval on the line is constant. Thus we may sensibly define
the gradient of l to be tanθ.
| y | x | x | |
|---|---|---|---|
| ℓ | |||
| θ | θ | ||
| 0 | |||
| positive gradient | negative gradient | ||
| 0◦< θ < 90◦ |
In the case where the line is parallel to the x-axis, we say that the gradient is 0. In the case
where the line is parallel to the y-axis, we say that θ = 90◦.
| 0 | x |
|
|
|---|---|---|---|
| zero gradient | |||
| θ not defined |
|
�cp,c |
�, | ||
|---|---|---|---|---|
|
||||
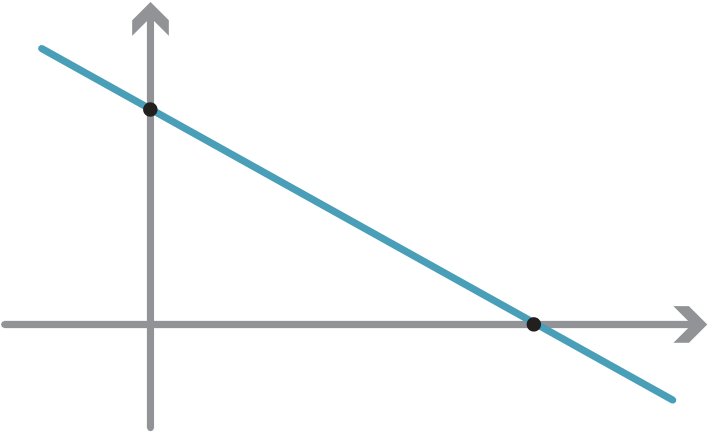
Intercepts and equations of lines
Intercepts
All lines, except those parallel to the x-axis or the y-axis, meet both coordinate axes.
y
(0,b)
ℓ
Consider the line l which passes through the point (x1, y1) and has gradient m.
y ℓ
| θ |
|---|
Let P(x, y) be any point on l, except for (x1, y1). Then
m =y − y1 x − x1 ,

{16} • Coordinate geometry
A special case is the line through (a,0) and (0,b), where a,b ̸= 0.
A guide for teachers – Years 11 and 12 • {17}
Summary
There are four different forms of the equation of a straight line which we have considered.
| y − y1 = m(x − x1) | |
| Gradient–intercept form |
|
|
{18} • Coordinate geometry
Vertical and horizontal lines
The equation of the vertical line through (3,4) is x = 3. The equation of the horizontalline through (3,4) is y = 4.
| 0 | x = 3 |
|---|
ℓ
n
| θ | θ |
|
|---|
A guide for teachers – Years 11 and 12 • {19}
|
|---|
|
b Find the gradient of the line which passes through the point (2,3) and the point of intersection of the lines 3x +2y = 2 and 4x +3y = 7.
Perpendicular lines
The lines y = mx +b and y = m1x +c are perpendicular if and only if mm1 = −1.
Proof
Suppose y = mx meets the x-axis at angle θ, that is, m = tanθ. For convenience, assume that m > 0. Then y = mx meets the unit circle at (cosθ,sinθ) in the first quadrant. If y = m1x is perpendicular to y = mx, then ∠AOB = θ, AB = sinθ, OA = cosθ and B is (−sinθ,cosθ). So
| m1 =cosθ−sinθ= − |
|---|
| � |
|---|
This result is often stated as:
The line y = m1x +c1 is perpendicular to the line y = m2x +c2 if and only if m1m2 = −1.
cos(A +B) = cos A cosB −sin A sinB
to show that
|
distance d of P from l?
y
| 0 | θ | ||||
|---|---|---|---|---|---|
|
|||||
|
|||||
s = −by1
−c .Thus
From the triangle, we have
| sinθ = | m �1+m2 . |
|
|---|---|---|
|
||
| sin2θ = | ||
From the first diagram, we now have
| a | ||
tion x +2y −10 = 0 and hence show this line is a tangent to the circle.
b Find the perpendicular distance from the centre of the circle to the line with equa- tion x +2y −12 = 0 and hence show the line does not meet the circle.
If a point P(x, y) lies on the circle with centre
| above, then P lies on the circle with centre | x | |
|---|---|---|
|
This is an example of a locus problem.
m =c − a b −d.
The line l goes through the midpoint�a +c ,b +d 2 �of PQ. Thus the equation of l is
{26} • Coordinate geometry
P(a,b)
Exercise 11
Use the locus method illustrated in the previous example to find the equation of the per-pendicular bisector of the line segment PQ, where the coordinates of P and Q are (−1,6) and (3,4).
The locus is two intervals parallel to AB together with two semicircles of radius d with centres A and B.
C(x3,y3)
A(x1,y1)
B(x2,y2)
| P | R | Q |
|
|---|
| ∆ = | ���������� | 1 | 1 | ���������� |
|
||
|---|---|---|---|---|---|---|---|
|
x2 | x3 | |||||
| y2 | y3 | ||||||
A guide for teachers – Years 11 and 12 • {29}
Links forward
In 3-dimensional space, things are more complicated:
• two points still determine a line
Two planes are parallel or meet in a line. Indeed, if two planes have a point in common, they must have a whole line of points in common (this is not obvious).
To set up a coordinate system for solid geometry, choose a plane 0xy and then fix axes 0x and 0y as in plane geometry.
| 0 | x |
|---|
Thus 0x ⊥ 0y, 0x ⊥ 0z and 0y ⊥ 0z.
| • |
|
|---|---|
| • |
P(x,y,z)
A(a,b,c)
x = td +(1− t)a
y = te +(1− t)b
z = t f +(1− t)c,
for t ∈ R. This is the parametric form for a line in R3. If t = 0, then P = A and, if t = 1, then P = B.We can obtain the Cartesian form for the line by eliminating t. It is
Consider the set
Π =�(x, y,z) ∈ R3| 3x +2y = 6�.
| 0 | (2,0,0) | |
|---|---|---|
| (a,b,0) |
However, if (a,b,0) is any point on this line, then (a,b,z) ∈ Π for any value of z. Thus Π is
a plane in R3. Indeed Π is a plane parallel to the z-axis. In a similar way, 3y +2z = 6 is a
through the points (4,0,0), (0,6,0) and (0,0,3), so the plane has three intercepts!
z y
where at least one of a,b,c is non-zero. |
|---|
A guide for teachers – Years 11 and 12 • {33}
Quadratic equations and the conics
Consider the set
S =�(x, y) ∈ R2| ax2+2hxy +by2+2g x +2f y +c = 0�,
{34} • Coordinate geometry
Example 3 (Two lines)
The equation x2−y2= 0 factorises as (x+y)(x−y) = 0, so y = −x or y = x. So this example is the union of two lines.
y
y = x
| 0 | x |
|---|
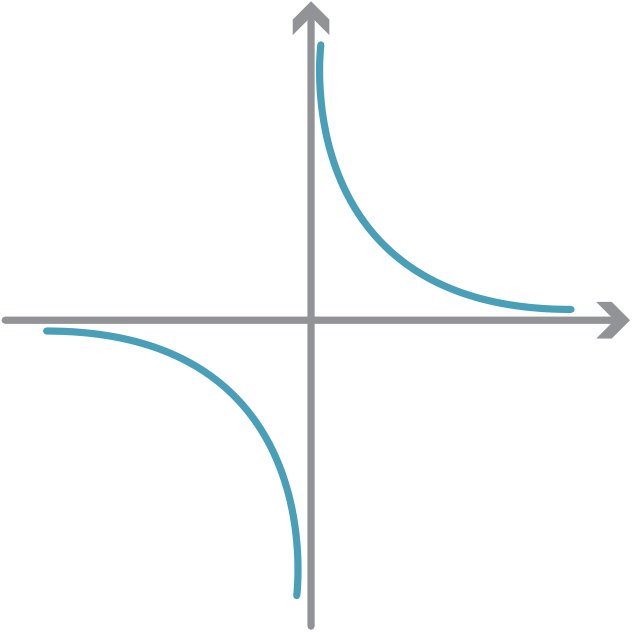
A guide for teachers – Years 11 and 12 • {35}
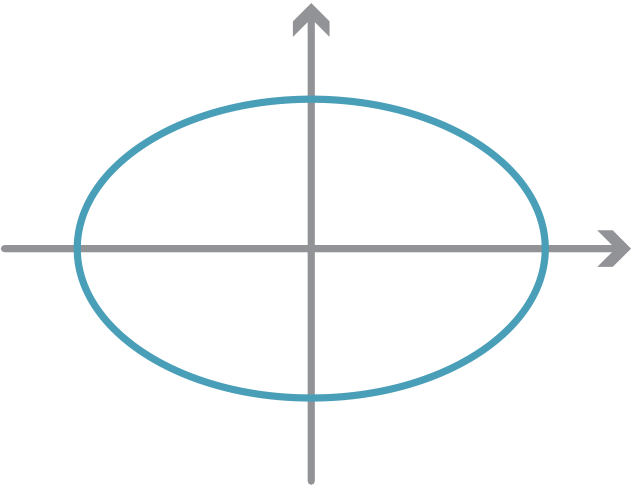
a2 + y2 b2 = 1, for a > 0, b > 0,
is an ellipse. It is a circle if a = b.
| –a | y | 0 | a |
|---|
a2 − y2 b2 = 1, for a > 0, b > 0.
By setting x = 0, we see there are no y-intercepts. If y = 0, then x = ±a.
y
x2 =4ay
| z | y |
|---|
A horizontal plane meets the cone in either one point or a circle. All the other examples in
our picture gallery (except the empty set) occur when different planes intersect the cone!
sic geometrical nature of S. Unless a = b = 0 (in which case S is a rectangular hyperbola), a rotation can be found which reduces S to either
History and applications
There were three facets to the development of coordinate geometry:
Apollonius of Perga (262–190 BCE) dealt with problems in a manner that may be called a coordinate geometry of one dimension, with the question of finding points on a line that were in a ratio to the others. The results and ideas of the ancient Greeks provided a motivation for the development of coordinate geometry.
Coordinate geometry has traditionally been attributed to René Descartes (1599–1650) and Pierre de Fermat (1601–1665), who independently provided the beginning of the subject as we know it today.
So P divides AB in the ratioa b: 1. Thus
| x = | x1 +a bx2 |
|---|
Exercise 2
Without loss of generality, assume PB = 1. Then
AC = AP cosθ
x − x1 = k x2−x1 k +1
(x − x1)(k +1) = kx2 −kx1
x =x1+kx2 k +1 .From the same diagram, we have CP = AP sinθ. Proceed in a similar way to find y.
The midpoint D of BC is
| �x2 |
|
|---|

Q A(8,10) P M B(18,20)
| P is | �3×8+2×18 | � | ||
|---|---|---|---|---|
| Q is | �3×8−2×18 | � |
|
Thus
The angle sum formulas give
sin(θ +90◦) = sinθ cos90◦+cosθ sin90◦= cosθ
cos(θ +90◦) = cosθ cos90◦−sinθ sin90◦= −sinθ.
| 1 tanθ. |
|
|---|---|
Conversely, suppose mm1 = −1, where m = tanθ. Then
|
|---|
| b |
|
|---|
A guide for teachers – Years 11 and 12 • {41}
Exercise 10
Note that a point (x1, y1) lies on the line l if and only if ax1 +by1 +c = 0.
Suppose that points (α,β) and (γ,δ) are on the same side of l. Then the line segment from (α,β) and (γ,δ) does not cross l. So ax1 +by1 +c ̸= 0 for each point (x1, y1) on the line segment. Thus the expression ax1 +by1 +c cannot change sign as the point (x1, y1) moves along the line segment from (α,β) to (γ,δ). Hence the signs of aα + bβ + c and aγ+bδ+c are the same.
The area of the triangle is
| ���1 | �6(5−7)+8(3−5)+2(7−3)���� = | ���−12−16+8 |
|
|---|
H
| B | C |
|---|
Similarly, AEBD is a cyclic quadrilateral and ∠D AB = α.
From △ABD, ∠ABD = 180◦−90◦−α = 90◦−α. Finally, in △CBF, ∠BFC +α+90◦−α = 180◦, so ∠BFC = 90◦, as required.
2a +b = 3 (3)
3c −2d = −1. (4)
We have found that A is (a,b) = (1,1). So the gradient of the line l is m =1−3
l has equation y −1 = 2(x −1) or, equivalently, y = 2x −1. 1−2= 2. Thus
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|


