Where the mass the disk and isthe radius the disk
|
Δ t |
|---|
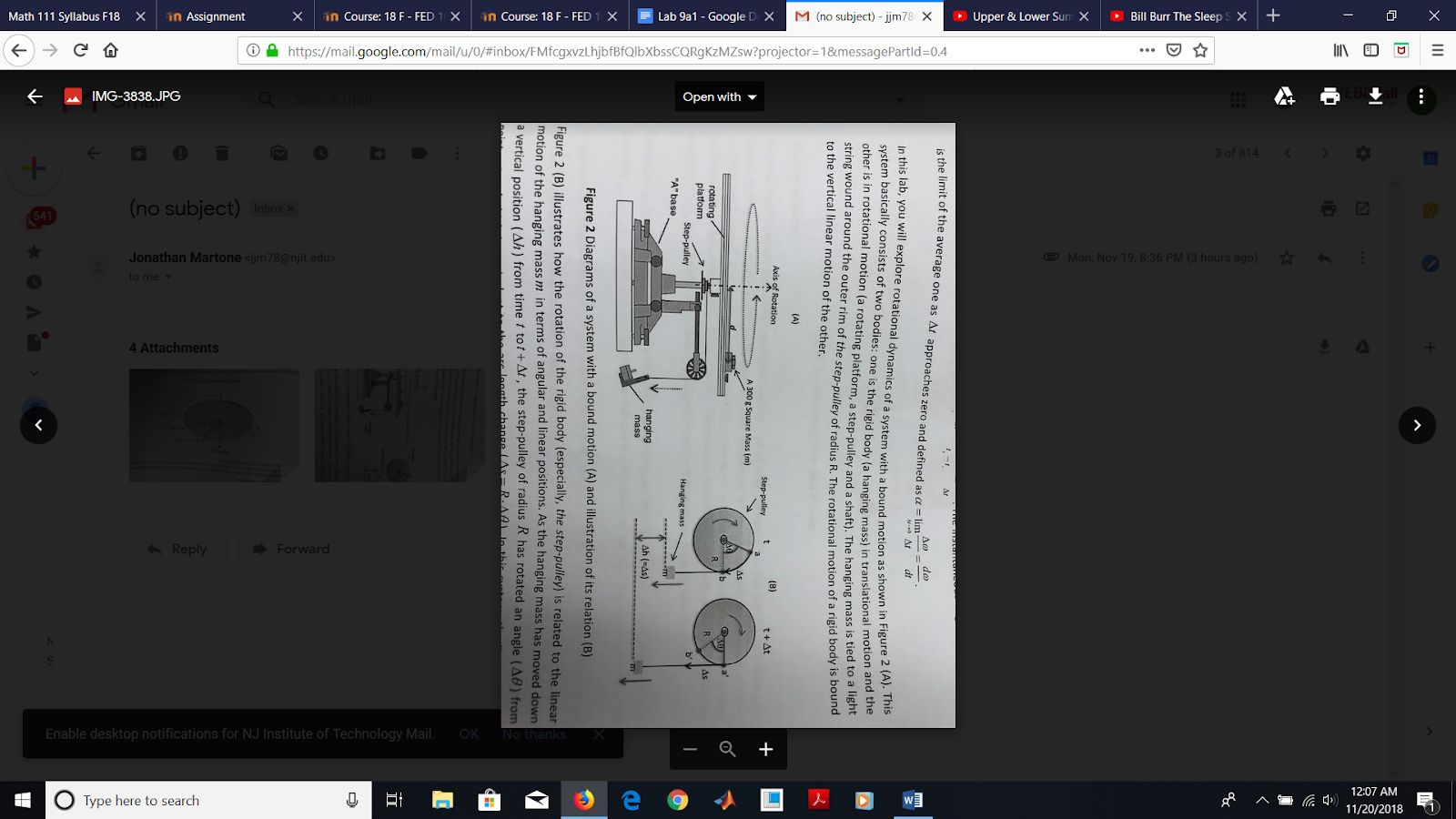
(a hanging mass) in translational motion and the other is in rotational motion (a rotating
platform, a step-pulley and a shaft). The hanging mass is tied to a light string wound
positions. As the hanging mass has moved down a vertical position (h) from time
t tot + t the step-pulley of radius R has rotated an angle ( Δθ) from point a to a'which is
Similarly, the acceleration (a) of the hanging mass is equal to the tangential acceleration (
aa ) of the point a at the rim of the step-pulley, which is equivalent to the radius R times
case 2, it is connected to the large one of radius R.
Moment of inertia
the radius of the disk. The rotational inertia I of a ring: R1 andR 2 are its inner and outer
radii, respectively.
through their center of mass.
Now you might have a question: how about the rotational inertia of a body when its axis
| Ir = ICOM + M | d , whereI 2 | COM |
|---|
center of mass, M is the mass of the object and d is the distance between its axis of
rotation and center of mass (Figure 5(B)).
expressed as K E total= K E translation+ K E rotation=2 1 mv 2 +
2I total ω , where m, v, Itotal andω are mass, linear velocity, total moment of inertia, and angular velocity of the body,
gravitational potential energy (PE) of the hanging mass m at rest is equal to the sum of its
translational kinetic energy and the rotational kinetic energy of the rotating body at the
rotational inertia), the string is massless and inextensible and the system is frictionless in
order to simplify the energy calculation. With use of the above equation, we can
The main goal of this lab is to experimentally determine the moment of inertia of an object with the help of the law of conservation of energy and compare it to the theoretically calculated one.
Part I: Measure the physical quantities of objects used in this experiment.
Part II: Theoretical determination of the moment of inertia of an object
1. Calculate the rotational inertia when each of two point masses (the 300g square mass) is positioned equally apart from the rotational axis by d distance. The d value will be given by your instructor.2. Calculate the rotational inertia of the disk when it rotates around its center of mass (refer to Figure 5(A)).
1. Have a set up as shown in Figure 8A.
2. Hang the mass hanger with a weight of 50 (or 100g) at the end of the string. 3. Wind the string around the rim of the 2nd pulley from top of the ste pulley by gently turning the rotating platform until the mass haner is close to the spoke pulley. Hold the rotating platform stationary.
8. Find out the angular acceleration (⍺) of the rotating body and linear acceleration (a) of the hanging mass in the plot. Describe how you find these values and what relation you observe between them.
9. Repeat the above steps for other rotating bodies (refer to Figure 8 B, C, and D). you should use the same value of distance d as used in Part II for the two point masses and the disk with rotation axis off its center of mass.
|
|
|---|---|
|
|
|---|---|
|
|
|
|
||
|---|---|---|---|
|
|
||
|
|
|
|
||
|---|---|---|---|
|
|
||
|
|
| 3.2 Calculations | i | 2 + 0 .5I | total | ω i | total | |||
|---|---|---|---|---|---|---|---|---|
| PE = mgh → .5mv | ||||||||
| Rod: | (0.1)(9.8)(0.1102) = .5(0.1)(0.0537) 2 + 0 .5I | |||||||
| total |
|
|||||||
|
total | |||||||
I Theoretical = m 1 d 2 + m 2 d 2 = ( .2792)(.15) 2 + ( .2782)(.15) 2 = 0.01254
(0.1)(9.8)(0.0589) = 0 .5(0.1)(0.0270) 2 + 0 .5I total (2.157) 2 = 0.02479
I = I total-I rod = 0.01317
I avg = (0.01249+0.01216+0.01317)/3 = 0.01261
I = I total-I rod = 0.00095
(0.1)(9.8)(0.0589) = 0 .5(0.1)(0.0069) 2 + 0 .5I total (0.556) 2 = 0.37343 |
|||
|---|---|---|---|
I = I total-I rod = 0.36113 |
total | (2.238) 2 | |
| total | (2.679) 2 |
|
|
I = I total-I rod = 0.03809
I avg = (0.36113+0.02611+0.03809)/3 = 0.14178
% Error: (Experimental - Theoretical) / Theoretical * 100 → 111.01%The graphs allowed us to determine both angular and linear acceleration in the system. Acceleration of course can be determined knowing that it is the change in velocity over a given time. With this, knowing conservation of energy in a system, we could then solve for I, the moment of inertia.
Generally, our percent error values when comparing the theoretical and
experimental values for the moment of inertias were high. One of the percent errors was less than 1% however the other two were close to 100%. These percent errors were caused by human error (further discussed in Question 4). Regardless, the group
successfully understood how inertia works and therefore the results met the objectives for the lab.Yes, there is a relationship between the angle of change of the rotating body with the linear position change of the hanging object. Because the angular position of the rotating body was dependant on the tension force of the string attached to the falling mass, the length of string extended, L, was related to the angle, theta, if, given the circumference of the pivot = C, L/C=theta/360.
3) It is assumed that the system in this experiment is frictionless which means that there is no energy loss due to friction. However, what if there is friction involved in this system? Explain how to modify the equation of the law of conservation of energy.
V. Conclusions
During this lab our group conducted experiments in order to explore the rotational motion of rigid bodies, done with respect to angular position and velocity, at a constant
acceleration. Additionally, we evaluated the relationship between angular and linear quantities of position and velocity. Keeping in mind the law of conservation of energy, we were finally able to, both theoretically and experimentally, determine the moment of inertia for various objects in different situations. This included the moment of inertia of two point masses and a disk (on and off of it’s center). Overall, percent error values were on the higher side and if human error was to be eliminated the results would have been better. Like all experiments involving motion, the experiment would benefit from being done in a way to minimize friction, perhaps by always ensuring that the pulley and pivot are rotating as freely as possible before the experiment is conducted.

