Wherea non-zero matrix reduced row echelon form
Student No.: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Important notes:
• A good strategy is not to spend too much time on any question. Read them through first and attack them in the order that allows you to make the most
progress.
|
10 pts | |||||||
|---|---|---|---|---|---|---|---|---|
|
A = | 2 | −5 2 | 0 |
2 |
3 subpts | ||
| 1 | 4 | |||||||
| 0 | 0 | 1 | ||||||
| 3 | −3 | 4 | ||||||
| (a) Find the reduced row echelon form of A. | ||||||||
Solution
| x1 | = | |
|---|---|---|
| x2 | = | |
| x3 | ||
| x4 | = | |
| x5 |
MATH1115 - Book B, Page 2 of 15
In vector parametric form,
a5 = 5a1 − 3a2 + 2a4
|
|---|
Hence columns 1, 2 and 4 of A form a basis for the column space of A. So a basis for col(A) is given by the three vectors
|
, |
1 |
, | 1
|
|---|
(a) Is the subset of R2defined by
H =��x
y� ∈ H , then the scalar multiple
(−1)�x
t − 1
s + t : s, t ∈ R
is really the span of two vectors:
K =
1 : s, t ∈ R
K ? 2 subpts
Solution
K is a plane in R3through the origin so it is the solution space to a
| A = | 0 |
b |
|
|
|---|---|---|---|---|
| 0 | ||||
| 0 | ||||
|
||||
| A = |
|
|
||
|
||||
−1 2 1 −1 2 2 −1 −1 1 | | | 1 0 0 0 1 0 0 0 1 −−−−−→ R1←R1/2
−1 1 1 −1 1 2 −1/2 −1 1 | | | 1/2 0 0 0 1 0 0 0 1 −−−−−−−−−−−−−−→ R2←R2−R1, R3←R3+R1
We can read off the inverse as1 0 −1 1 0 1
You should check that this is the inverse by calculating the product of the initial1 0 2.
| −1 1 | 0 12 |
1 |
2 | 0 |
0 |
|
||
|---|---|---|---|---|---|---|---|---|
| 2 | 1 | |||||||
| 0 | −1 | 0 |
Let A be the n × n standard matrix associated with T . Then we have that Au = Av and rearranging, A(u − v) = 0. We know u ̸= v, so we see that A has non-trivial solutions to Ax = 0. By the invertible matrix theorem, this means A is not invertible, and also implies that A (and T ) cannot map onto Rn.
We can also argue directly that an n × n matrix with non-trivial solutions to Ax = 0, must have a free variable. Then the number of pivot columns for A is strictly less than n, so the columns of A cannot span the whole of Rn, which means T is not onto.
Solution
Rearrange the equation to get A3+3A2= 6I then factorise to get A(A2+3A) = 6I . We now have an expression of the form AB = I . Since A is square, by the
Solution
2f + c
2f i������� |
|---|
| cx | + | az | = | |
|---|---|---|---|---|
| bx | + | ay | = | |
| cy | + | bz | = |
(i) Show that the matrix for this system of linear equations has a non-zero determinant.
(ii) Use Cramer’s rule to solve for the unknown z.
(ii) Cramer’s rule for the third unknown z, is z = det A3(b)/ det A where
| A3(b) = | c |
0 | |
|---|---|---|---|
| a | |||
| c |
z =c(a2 + b2 − c2)
2abc=a2 + b2 − c2
2ab
(d) Let S be the tetrahedron in R3with vertices at (0, 0, 0), (1, 0, 0), (0, 1, 0) and
(0, 0, 1), and let S′be the tetrahedron with vertices at vectors 0, v1, v2, v3.
Solution
(i) The linear transformation, T , that maps S onto S′has standard matrix
height of S is 1 unit, and the area of the base is the area of a right-angled triangle
with edges of length 1 unit, so
MATH1115 - Book B, Page 12 of 15
| 10 pts |
|---|
| z2= 1 + i√3, | and |
|
|---|
(Recall that there are n nth-roots of a complex number). The rule for finding all complex numbers z such that zn= w is:
MATH1115 - Book B, Page 13 of 15
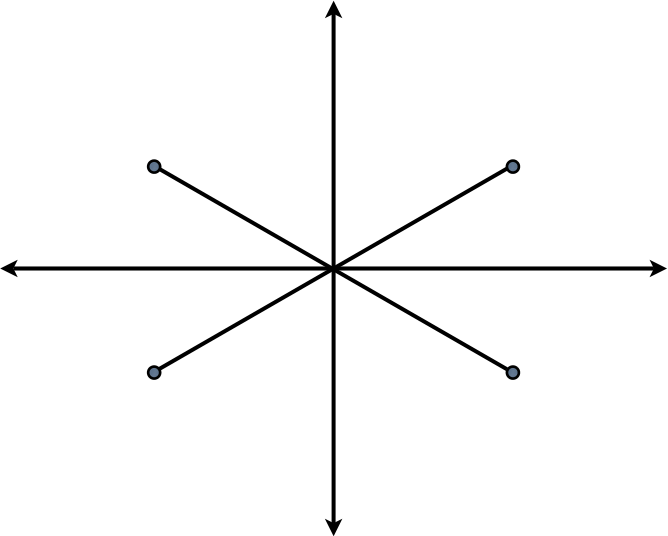
| z1 | = |
|
|
|---|---|---|---|
| = | |||
| z2 | = | ||
| z3 | = | ||
| z4 | = | ||
z3 z1
Re(z)
(iii) Hence show that the sum of the n n-th roots of 1 is equal to zero. Hint: You might find the partial sum formula useful.
| zk = (1)1/n | �cos | �2πk | � | + i sin | �2πk |
|
|---|
for k = 0, 1, . . . , n − 1.
So the above expression for the sum evaluates to zero.
