Xyz xyz xyz xyz xyzthe karnaugh map contains rectangles and rectangles

Minimal Sum of Products (MSP) Form & Karnaugh Maps

Chapter 10: Boolean Algebra (continued)

Minimal Sum of Products: Terminology▶ A literal is any variable x or its complement x′.▶ A fundamental product is any product of literals.

▶ A literal is any variable x or its complement x′.▶ A fundamental product is any product of literals.

Examples

Examples

Examples

Minimal Sum of Products
Definition

Minimal Sum of Products
Definition

Minimal Sum of Products
Definition

Minimal Sum of Products
Definition

Example

Finding the MSP form

▶ This can be viewed as a Boolean algebra analogue of truth tables for propositions.

Finding the MSP form

▶ A Karnaugh table for a Boolean expression in n variables is a rectangular table with 2nentries, one for each of the possible minterms.

Karnaugh Tables

▶ The table is arranged so that entries corresponding to any two minterms that differ in just one variable are adjacent (i.e., they share a common edge).

Example: The minterms xy′z and x′y′z differ in just the x variable, whereas xyz and x′yz′differ in both x and z.

▶ The rows and columns of a Karnaugh table are labelled (so that the adjacency requirements are satisfied) and the label of any entry is the“product” of the corresponding row and column labels.

Karnaugh table for expressions in two variables

Karnaugh table for expressions in two variables

Karnaugh table for expressions in four variables

Karnaugh’s method for finding MSP’s
▶ Each square or entry in a Karnaugh table corresponds to a minterm.

▶ Each square or entry in a Karnaugh table corresponds to a minterm.

▶ So we can regard a collection of squares in a Karnaugh table as a sum of minterms.

▶ The Karnaugh map of a Boolean expression is the collection of squares in a Karnaugh table corresponding to its disjunctive normal form.

We mark each of these squares with a + (or some other symbol) to highlight them.

We mark each of these squares with a + (or some other symbol) to highlight them.

So there is one + symbol for each minterm in the DNF.

Examples
Karnaugh map of the DNF xy′z + xyz′+ x′yz + x′y′z + xy′z′+ x′yz′:

Examples
Karnaugh map of the DNF xy′z + xyz′+ x′yz + x′y′z + xy′z′+ x′yz′:

Examples
Karnaugh map of the DNF xy′z + xyz′+ x′yz + x′y′z + xy′z′+ x′yz′:

Examples
Karnaugh map of the DNF xy′z + xyz′+ x′yz + x′y′z + xy′z′+ x′yz′:

Note:
▶ You do not need to convert an expression to DNF before drawing its Karnaugh map.

Note:

Draw the Karnaugh map of the expression E = x + (y ↓ z).

Examples . . .

Draw the Karnaugh map of the expression E = x + (y ↓ z).

First we convert E to a sum of products:

Examples . . .

Now we draw the map of the sum of products form of E by referring to the expression x + y′z′summand by summand.

First we convert E to a sum of products:

The first summand is x, so we put a + in every square of the table that has an x in its row or column label.

Examples . . .

Now we draw the map of the sum of products form of E by referring to the expression x + y′z′summand by summand.

First we convert E to a sum of products:

The next summand is y′z′, so we put a + in every square that has both y′and z′in its row or column label.

Examples . . .

Now we draw the map of the sum of products form of E by referring to the expression x + y′z′summand by summand.

First we convert E to a sum of products:

Thus the Karnaugh map of E has five squares highlighted.

We can read off the DNF form of E:

Karnaugh Maps . . .

▶ Karnaugh maps are useful for finding MSP forms because the Karnaugh maps of fundamental products are easy to recognise.

▶ The Karnaugh map of a fundamental product is called a
fundamental rectangle, or a 2s-rectangle if it contains 2ssquares.

Fundamental Rectangles: Examples

Map of x

Fundamental Rectangles: Examples

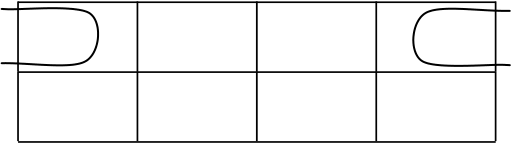
Fundamental Rectangles: Examples . . . Some fundamental rectangles in three variables

wx′

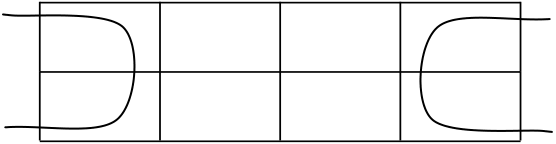
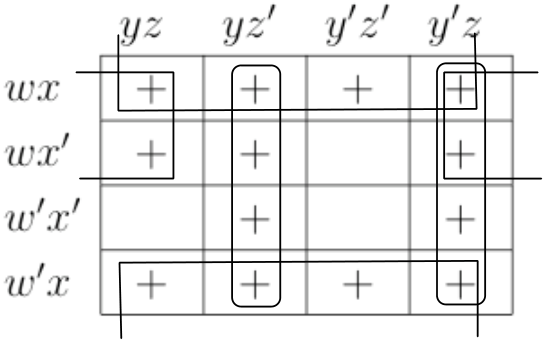
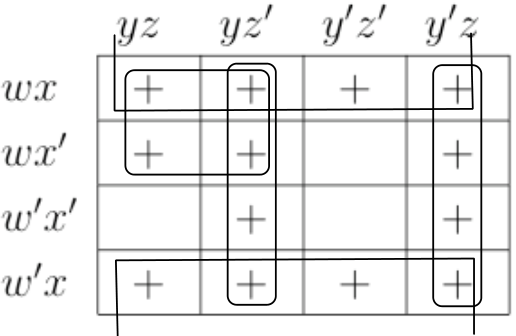
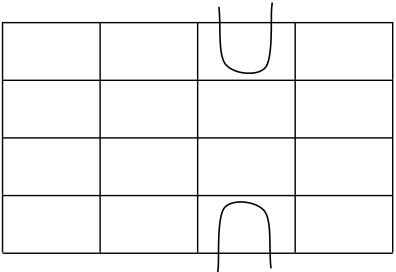
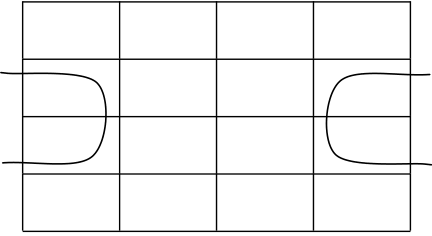
Fundamental Rectangles: Examples . . . Some fundamental rectangles in four variables

	MAS162 – Foundations of Discrete Maths			14

This results from the adjacency conditions that we mentioned earlier.

Fundamental Rectangles . . .

This results from the adjacency conditions that we mentioned earlier.

▶ Also note that the size of the rectangle for a fixed fundamental product depends on the number of variables.

▶ Also note that the size of the rectangle for a fixed fundamental product depends on the number of variables.

▶ That is, if we are considering Boolean expressions in n variables, then a fundamental product consisting of m of those variables corresponds to a fundamental rectangle consisting of 2n−msquares.

▶ Also note that the size of the rectangle for a fixed fundamental product depends on the number of variables.

▶ That is, if we are considering Boolean expressions in n variables, then a fundamental product consisting of m of those variables corresponds to a fundamental rectangle consisting of 2n−msquares.

▶ Also note that the size of the rectangle for a fixed fundamental product depends on the number of variables.

▶ That is, if we are considering Boolean expressions in n variables, then a fundamental product consisting of m of those variables corresponds to a fundamental rectangle consisting of 2n−msquares.

Finding an MSP form of a Boolean expression We cover the K-map with:

▶ the fewest number of rectangles in order to minimise the number of summands; and

We start with the largest fundamental rectangles and work down to the smallest.

Finding an MSP form of a Boolean expression We cover the K-map with:

Example

▶ the largest rectangles in order to minimise the total number of literals.

We start with the largest fundamental rectangles and work down to the smallest.

Finding an MSP form of a Boolean expression We cover the K-map with:

▶ the fewest number of rectangles in order to minimise the number of summands; and

We start with the largest fundamental rectangles and work down to the smallest.

Example

▶ the fewest number of rectangles in order to minimise the number of summands; and

▶ the largest rectangles in order to minimise the total number of literals.

Procedure to find MSP forms using Karnaugh maps To find an MSP form for a Boolean expression in n variables:

Procedure to find MSP forms using Karnaugh maps To find an MSP form for a Boolean expression in n variables:

Using Karnaugh maps to find MSP forms: Examples

Find an MSP form of each of the following Boolean expressions.

(a) f1 = y + xy′z

The chosen fundamental rectangles correspond to the fundamental

products y and xz.

So an MSP form for f1 is y + xz.

(b) f2 = xyz + xyz′+ xy′z + x′y′z′+ x′y′z

The Karnaugh map contains no 8-rectangles and no 4-rectangles, but

we can cover it by three 2-rectangles in two different ways.

The two MSP forms for f2 are xy + x′y′+ y′z and xy + x′y′+ xz.

The Kargnaugh map of f3 can be covered in two ways by one 8-rectangle and three 4-rectangles.

Examples . . .

▶ An MSP form is usually a useful simplification of a Boolean expression.

▶ However it is not always the very best.

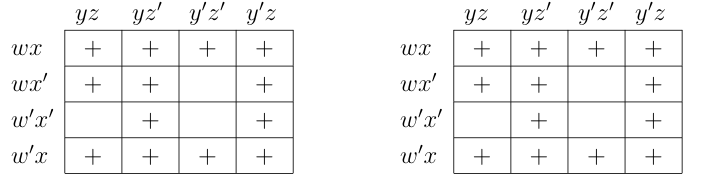
Consider the Karnaugh map of the Boolean expression (w ⊕ x) ⊕ (y ⊕ z).

Consider the Karnaugh map of the Boolean expression (w ⊕ x) ⊕ (y ⊕ z).

▶ Given the truth table of a Boolean expression E, consider the set of minterms that equal 1 for the rows where E = 1.

Connection with truth tables

Connection with truth tables . . . ▶ This is because the sum has value:

0 + · · · + 0 + 1 + 0 + · · · + 0 = 1
(where the 1 corresponds to a single minterm) when E = 1.

0 + · · · + 0 + 1 + 0 + · · · + 0 = 1
(where the 1 corresponds to a single minterm) when E = 1.

▶ Thus the sum of minterms is precisely the DNF of E.

0 + · · · + 0 + 1 + 0 + · · · + 0 = 1
(where the 1 corresponds to a single minterm) when E = 1.

▶ Thus the sum of minterms is precisely the DNF of E.

0 + · · · + 0 + 1 + 0 + · · · + 0 = 1
(where the 1 corresponds to a single minterm) when E = 1.

Example: DNF from a truth table
Consider the truth table of the Boolean expression f1 = y + xy′z (which corresponds to y ∨ (x ∧ ¬y ∧ z)).

Example: DNF from a truth table
Consider the truth table of the Boolean expression f1 = y + xy′z (which corresponds to y ∨ (x ∧ ¬y ∧ z)).

Example: DNF from a truth table
Consider the truth table of the Boolean expression f1 = y + xy′z (which corresponds to y ∨ (x ∧ ¬y ∧ z)).

Example: DNF from a truth table
Consider the truth table of the Boolean expression f1 = y + xy′z (which corresponds to y ∨ (x ∧ ¬y ∧ z)).

Hence the DNF of f1 is f1 = x′yz′+ x′yz + xy′z + xyz′+ xyz.

Example: DNF from a truth table
Consider the truth table of the Boolean expression f1 = y + xy′z (which corresponds to y ∨ (x ∧ ¬y ∧ z)).

These correspond to the five minterms: x′yz′, x′yz, xy′z, xyz′, xyz.

Hence the DNF of f1 is f1 = x′yz′+ x′yz + xy′z + xyz′+ xyz.