Measures of dispersion homework help

Measures of Central Tendency often centres around the centre of the data, and thus, there is always a chance that you might miss some consequential data due to this demerit. A measure of dispersion, therefore, focuses on the details around the centres. As the name suggests, it reads, measures and analyses the way variables are dispersed in the data set. Sometimes, it gets very important when the mean and median of two data being compared is the same even if the datasets are completely different. There are many methods to calculate dispersion, so get your measures of dispersion homework help, to both learn the application of these methods and the techniques for it.

There are mainly 3 methods of dispersions, whose basics will be covered here. More advanced level, you can get measures of dispersion assignment help, from the best tutors who will complete your homework and can provide samples and notes for the topic. These three methods of dispersions are range, interquartile range and standard deviation.

Range

The range is the most basic and simultaneously most demerited way for measurement of dispersion. Range of a data is calculated through the basic simple formula:

Range= Highest variable in the dataset - Lowest variable in the dataset

This method for measuring dispersion is very faulty and therefore often overlooked.

An example of a calculation can be made here.

A data set for marks of a student in five papers out of hundred marks is the following: 99, 89, 70, 83 and 65.

For the given set, Range= 99-65= 34.

Range, even though is simple to calculate, gets complex when stuck with data with different units and with frequencies. To get confusion-free with any concept relating to this, get measures of dispersion homework help from best minds. Talk to an expert on measures of dispersion homework and avail the best measures of dispersion assignment help online to secure A+ grades in your academics now!

Interquartile range

The interquartile range focuses on the range of a single or multiple quartiles. It is mainly used to calculate the middle 50% range dispersions, thus eliminating the 25% data on each extremity. The interquartile range is calculated through the use of quartiles. Quartiles, in a given set of data, are made by dividing into different parts and pieces. They could be ranged into making even the 100th part of the data. It is mainly used to divide the data into four blocks/parts. Each part is called quartiles, and the dividing positions are named Q1, Q2 and Q3 respectively.

The formula to calculate these quartiles are the following:

Q1 = n+1/4

Q2 = (n+1)*2/4 = n+1/2 (This, is therefore, similar to median.)

Q3 = (n+1)*3/4

An Interquartile range is calculated using the following formula:

Interquartile range= Q1- Q3

Interquartile range while focusing on data dispersion in the middle 50%, can also be used to calculate the same for other quartiles. The interquartile range is preferred over the range, as it eliminates the ‘ignorance of vast data’ which range usually suffers from.

An example for Interquartile Range:

11 students scored the following in their exams: 75, 81, 52, 92, 68, 78, 75, 45, 87, 90, 86.

First, we will arrange all the data given in ascending order. So the new data will be: 45, 52, 68, 75, 75, 78, 81, 86, 87, 90, 92.

Quartiles for the data will be the following:

Q1= = 11+1/4 3rd term= 68

Q2= = 11+1/2 6th term= 78

Q3= (11+1)*3/4 = 9th term= 87

So, the interquartile range will be;

Interquartile range= 87-68= 19

Interquartile ranges can vary on different data and could be calculated in different ways. To learn more about how and when to apply this method and to get notes and solutions or samples, get measures of dispersion homework help, where you will not only get on-time homework delivery but also accurate and non-plagiarised solutions.

Standard Deviation

Perhaps the most commonly used method, the standard deviation is used as a method to measure how to spread the numbers are. It is used to measure the discrepancies and variables of the data. Greek term Sigma (𝛔) is used to denote this term.

There are many formulas and methods to calculate the Standard Deviation. And each method or formula is used in specific conditions. To know more about different methods and their application, get your measure of dispersion homework help from experts. The commonly used formula to calculate Standard Deviation is:

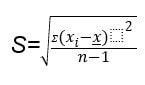
The process of calculating Standard Deviation is very complex and needs to also calculate Mean.

Step 1: Firstly, we calculate Mean in the data. We denote this term by the sign .

Step 2: Next we calculate the deviation of each variable. To do this, we subtract the mean from each data point.

Step 3: Square each deviation. So, all negative terms will become positive. 

Step 4: Add the square of each deviation.

Step 5: We calculate variance. To do this, we divide this data calculated in step 4, by the term you get by subtracting one from the number of data points.

Step 6: The square root of the variance achieved is called the standard deviation.

Sometimes, depending on the data set, the formula changes to:

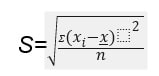
When is this applied? Some examples of solved standard deviation questions. Or some samples. For all of this and more, get your measure of dispersion homework help from experts who know how to deliver the quality assured, statistically accurate homework on time. Learn more from samples you get while availing measure of dispersion homework help.

We at Urgenthomework are committed to giving you the best services related to measures of dispersion homework help, if you have assignment or question related to measures of dispersion homework, you can best help in all of your academics anytime.

Avail measures of dispersion assignment help now to impress your friends and your professor.