300736 Concrete Structures

Question 1. (Total: 10 Marks)

For the singly reinforced beam section shown in Figure-1 calculate the ultimate moment capacity, M_{u .} Show detail calculation and express final result in kNm.

Given f_c^' = 50 MPa and f_sy = 500 MPa. All dimensions in Figure-1 are given in mm.

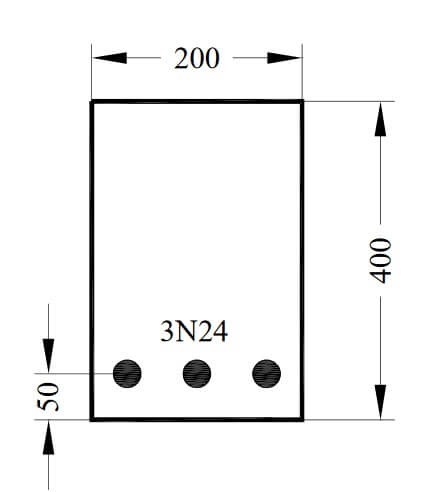
Figure 1

Question 2. (Total: 20 Marks)

The doubly reinforced concrete beam (T- Section) shown in Figure-2 is reinforced with 6N36 bars in tension and 2N24 bars in compression.

Given f_c^' = 32 MPa, and f_sy = 500 MPa. All dimensions in Figure-2 are given in mm.

1. Calculate the flange width, b where b = 900+20n

Take n = last digit of your student number. For example: student number 19025679, n = 9; b = (900 + 20*9)=1080 mm)

1. Determine the ultimate moment capacity of the T- section beam. iii) Checks for the yielding of tensile steel and compression steel.

(n = last digit of your student number)

b = 900+20n

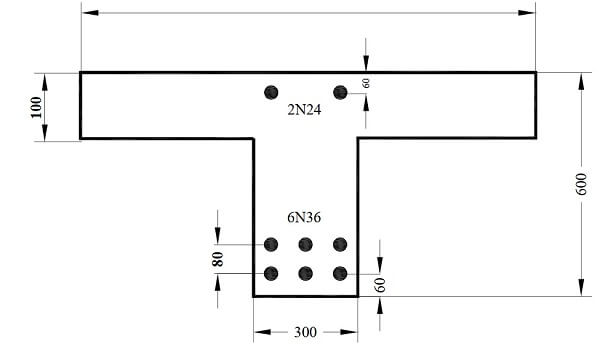
Figure 2

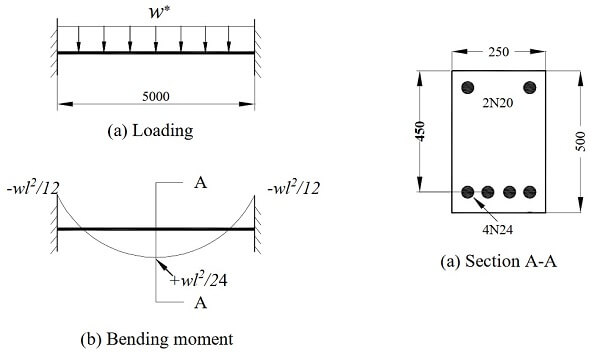
Question 3. (Total: 20 Marks)

A reinforced concrete beam supporting a storage floor. The beam carries a uniformly distributed (UDL) dead load of G = 25 kN/m and an imposed live load of Q = (8+3n) kN/m (where n is the last digit of your student number). The load, bending moment diagram and the beam section are given in Figure-3. 

Given, f_c^' = 40 MPa, f_sy = 500 MPa. All dimensions in Figure-3 are given in mm.

1. Calcualte the imposed live load, Q where Q = (8+3n) kN/m

Take n = last digit of your student number. For example: student number

19025679, n = 9; Q = (8 + 3*9)=35 kN/m)

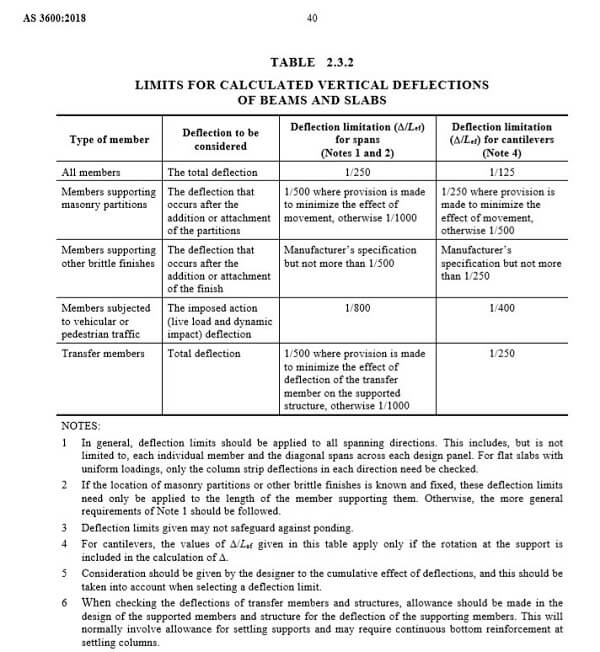
1. Determine the short term deflection (∆_s) at the mid section of the beam.

Figure 3

EXTRACTS FOR MID‐TERM TEST

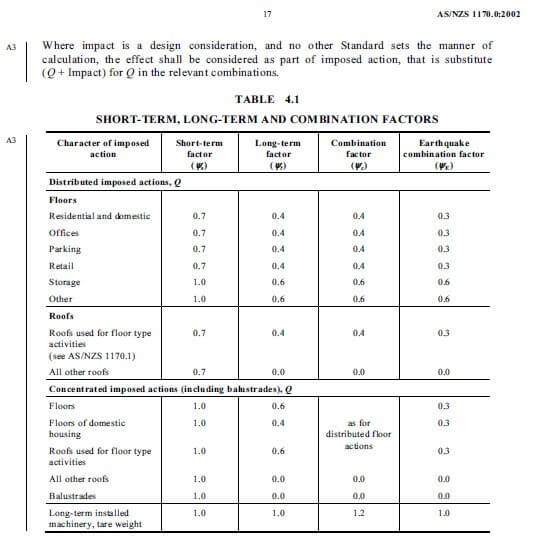
General

For transformed cracked section, singly reinforced beam