CENG 150 Electronic Circuits Lab 9 The Differential Amplifier

INTRODUCTION

We will examine the op-amp version of the differential amplifier. You will appreciate the relative simplicity of the op-amp version. You may also observe that this amplifier is actually a combination of the inverting and non-inverting amplifiers.

An image of your Tinkercad circuit is required (please insert in the correct position in the report) for each measurement section.

Note: Some parts produce a perfect result, as expected from a simulation software. In practice, a difference is expected.

THE EXPERIMENT

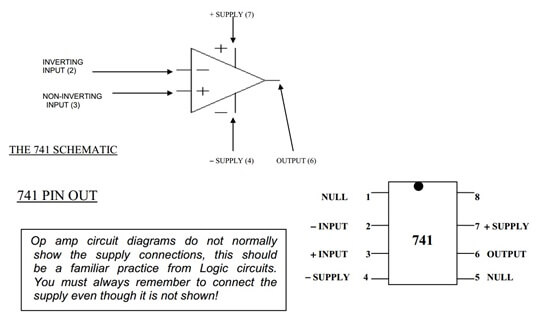
1. Setup the power supply to have ±10V dual voltage outputs.

2. Construct the circuit shown below; pay special attention to the ±10V voltage and the ground connections from power supply. Label the pin numbers to make your connection process clear.

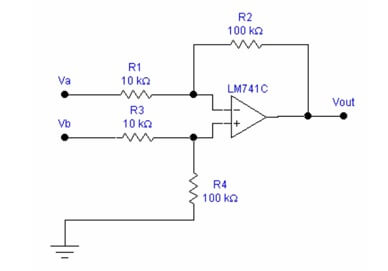
3. By the Superposition Theorem, we can measure the voltage output produced by a single input signal at a time; and the total output voltage will be the algebraic sum of each individual output voltage (or gain).

4. Measure the differential voltage gain A_va using superposition as follows:

a. Ground V_b;

b. Use the signal generator to generate the following signal and connect it to V_a:

1. Type of the signal: Sine waveform
2. Frequency: f = 1kHz;
3. Peak amplitude (Peak value): 5V
4. Offset DC voltage: 0V.

Use the oscilloscope to observe input V_a on channel 1 and output V_out on channel

Sketch the signal voltages observed on the oscilloscope in the following:

c. From the waveform on scope, find the peak-to-peak values of the signals on input and output, respectively:

V_a(PP) =

V_out(PP) =

d. Please circle the correct answer: the phase relationship between V_a and V_out is:

1. Out of phase or
2. In phase

e. Calculate the voltage gain A_VA based on your measurement (show your calculation procedures):

A_VA =

5. Don’t change the setting of the signal generator, repeat step 4 but this time with V_a grounded and apply the input signal to V_b. Record the peak-to-peak value of the signal and calculate the voltage gain A_VB(show your calculation procedures):

V_b(PP) =

Vout(PP)

A_VB =

6. Calculate the Average of the absolute value of the voltage gain A_VA and A_VB in step 4 and 5 and record it below (show your calculation procedures):

A_AVG(D) =

7. Now we can measure the common mode gain A_cm as follows:

1. Short V_a and V_b together.
2. Apply a large 1kHz sine wave to both V_a and V_b (e.g., 5V_peak) together.
3. Measure V_OUT carefully and determine the common mode gain A_cm (show your calculations), it should be <<<1. (You may see some noise in the output, just record the RMS value of the input/output and calculate the A_cm)

V_a(RMS) =

Vout(RMS)

A_cm =

8. Calculate the COMMON MODE REJECTION RATIO (CMRR) in dB:

CMRR = 20log(A_AVG(D)/A_CM)

9. The highest CMRR results will be reached when the resistors are perfectly matched. For the poorly matched resistors, the results could be very different. To illustrate the effect of poorly matched resistors, change your resistors R₃ and R₄ as follows (leave R₁ and R₂ untouched):

R3= 12KΩ R4= 82KΩ

10. Repeat the measurements above and then determine the CMRR in dB:

Average A_AVG(D) =

A_cm =

CMRR in dB =

11. Compare results in step 10 and step 7, did you see any difference in A_cm and CMRR?

QUESTIONS

1. Use the theory you have learned from class, derive the output voltage V_out in terms of V_a and V_b, assume R₁=R₃=10kΩ and R₂=R₄=100kΩ (Hint: You need to find the equation based on “virtual short”).
2. Repeat question a) when R1= 10KΩ, R2= 100KΩ, R3= 18KΩ and R4= 82KΩ.