COSC1107 Assignment 1

Computing Theory

COSC 1107/1105

Assignment 1: Fundamentals

1 Overview

This assignment is intended both for introducing you to some basic concepts that we will use in various ways later in the course, and to provide some early feedback on your progress. The are six key concepts that we will return to again and again, which are formal languages, regular expressions, grammars, finite state automata, pushdown automata and Turing machines. A common thread in all of these is nondeterminism. This will come up in various contexts, as you will see. Much of this assignment is concerned with these concepts, to ensure that you are well-versed in these fundamentals. There is another part which deals with the Platypus game.

2 Assessment details

A Note on Notation of Regular Expressions: Unfortunately there isn’t a uniformly accepted standard notation for regular expressions. Given we are using JFLAP, our notation should be as consistent as practicable with that, but that also means some things get quite cumbersome. The two main issues are the specification of alternatives, and how to abbreviate some obvious patterns like letters and numbers. So in this assignment the following syntactic rules will be used.

’+’ will be used to denote both alternatives (as in (1+2)^∗) and also to denote one or more applications of Kleene star. You must take its application within the context in which it is applied (so you will need to use your brains!).

Ranges such as all letters or all digits will be represented as [a−z] meaning (a+b+ c+d+e+f +g+h+i+j+k+l+m+n+o+p+q+r+s+t+u+v+w+x+y+z).

Hopefully the reason for using ranges is now obvious!

A. Regular Expression and languages. (20 marks)

The Ministry of Craziness uses email addresses of the form

[a − z]([a − z] + [A − Z] + [0 − 9])^∗@(([a − z])⁺)^∗moc.com

and employee identifiers of the form

moc([0 − 9])⁺@moc.com

a. Explain why there are email addresses which are also employee identifiers.

Give at least three examples. (3 marks)

b. Explain why both of the strings gandalf@a4com and Gandalf@magicmoc.com are neither email addresses nor employee identifiers. (2 marks)

c. In the company archives, the following regular expression has been found. Explain what the language of this expression is in terms of email addresses and employee identifiers. Is the empty string in this language? (3 marks)

([a − z]([a − z] + [A − Z] + [0 − 9])^∗ @ (([a − z])⁺)^∗moc.com + moc([0 − 9])⁺@moc.com)^∗

d. A director of the Ministry of Craziness, the Cut Snake, wants to change this arrangement so that employee identifiers are now of the form

moc([0 − 9])⁺

and that email addresses will now be of the form

(moc([0 − 9])⁺ + [a − z]⁺)@moc.com

Which email addresses are unaffected by this change (i.e. satisfy both definitions)? Which old email addresses are no longer valid? Explain your answer, including examples. (3 marks)

e. The Ministry of Craziness, and especially the the Cut Snake, have some specific rules about phone numbers. These are below.

Mobile numbers have exactly 9 digits, commence with 0 or 9 and must end with 321.

Landline numbers have at least 4 digits, and must not finish with any of the digits 0, 2, 4, 5, 6, or 8.

Franchise numbers have exactly 6 digits, and commence with either 22 or 44.

Nothing else is a phone number.

Give a regular expression for mobile numbers, another one for landline numbers and a third one for franchise numbers. (3 marks)

f. Are there any phone numbers which are both mobile numbers and landline numbers? Explain your answer. (2 marks)

g. Are there any phone numbers which are both landline numbers and franchise numbers? Explain your answer. (2 marks)

h. The Cut Snake then decrees that all sequences of numbers (such as the Ministry’s list of phone numbers) must be ordered in such a way that any mobile number is followed by at least two franchise numbers, and any landline number is immediately preceded by a single franchise number. If M, L and F are regular expressions for mobile, landline and franchise numbers respectively, give a regular expression in terms of M, L and F that specifies legal sequences of numbers. (2 marks)

B. Grammars. (17 marks)

a. Consider the G grammar below.

S → aSbb | aA

A → ccA | B B → Bd | λ

Give a derivation of a string in L(G) which contains at least 4 occurrences of a. (2 marks) ii. Give a derivation of length at least 8 of a string in L(G). (2 marks) iii. Is λ ∈ L(G)? Explain your answer. (1 marks) iv. Express L(G) in set notation. (3 marks)

b. The Cut Snake University provides students with identifiers of the form

csu − N − P

where

N is a student number in quaternary (ie each digit is either 0, 1, 2, or 3) whose length is even and at least 4, and for which the last digit is 3

P is a program specifier, also in quaternary, and whose length is an even number which is at least 2, and whose first digit is 1

For example, csu − 3003 − 13 and csu − 310213 − 1230 are valid identifiers.

Give a grammar whose language contains all valid Cut Snake University identifiers, and only such identifiers.      (2 marks)

c. Give the derivation in your grammar for the two identifiers above. (2 marks)

d. The Cut Snake himself then decrees that all student numbers and all program specifiers must be palindromes (numbers which are the same when reversed).

Give a grammar for this new version of identifiers. (3 marks)

e. Given the derivation in your grammar above for the (new) identifiers csu −

3113 − 1221 and csu − 321123 − 123321. (2 marks)

C. Finite State Automata. (15 marks)

a. Consider the finite state automaton M You can download this from Canvas here.

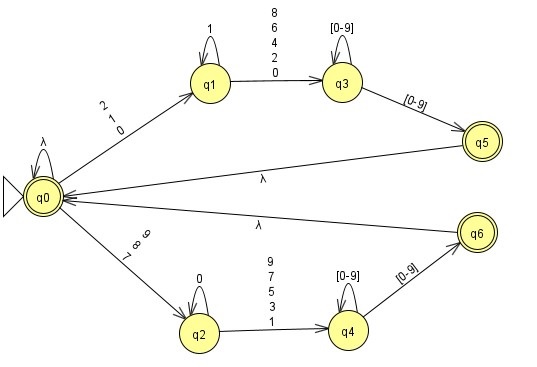
i. Give three examples of strings in L(M). (1 mark)

ii. Give three examples of strings not in L(M) of length at least 4. (2 marks)

iii. Is this machine deterministic? Justify your answer. (2 marks)

iv. What is L(M)? Explain your answer. (4 marks)

b. Your student number is a sequence of 7 digits. Construct a finite state automaton (deterministic or otherwise) which accepts a sequence of digits if it is an even number of occurrences of the last four digits of your student number. For example, if your student number is 7654839, you should describe how to construct an automaton which will accept the strings 48394839 and 4839483948394839 but not 4839and not 4839124839 and not 48394839 As part of your answer show the JFLAP output for at least three strings accepted by the machine and at least three strings of length 4 or more rejected by it. (4 marks)

c. Consider now the problem of constructing a similar automaton, but one accepts any string which contains an even number of occurrences of the last four digits of your student number. For example, this machine should now accept 4839124839 and 4839483912 but not 4839. How would you construct this machine? Explain your answer. (2 marks)

D. Pushdown Automata (12 marks)

Consider the PDA M₁ below. You can download this from Canvas here.

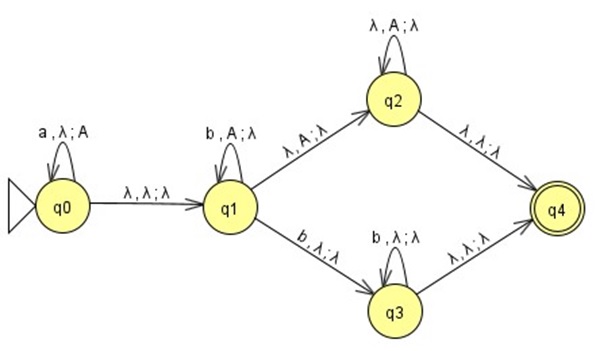
• Show the execution of the strings aabbb, aaabb and aaabbb in M. (3 marks)
• What is L(M₁)? Explain your answer. (3 marks)
• Construct a PDA M₂ such that L(M₂) = {w|w ∈ {a,b,c}^∗,n_a(w) = n_b(w)}. (4 marks)
• Given any two PDAs M₁ and M₂, it is straightforward to construct a PDA M₃ such that L(M₃) = L(M₁) ∪ L(M₂). Given the two PDAs M₁ and M₂ above, is there a simpler PDA for this language? Explain your answer. (2 marks)

E. Turing machines (17 marks)

Consider the Turing machine M₁ below. You can download this from Canvas here. Note that the input alphabet is {7,8,9} and the tape alphabet is {1,2,7,8,9,B} where B is the blank symbol.

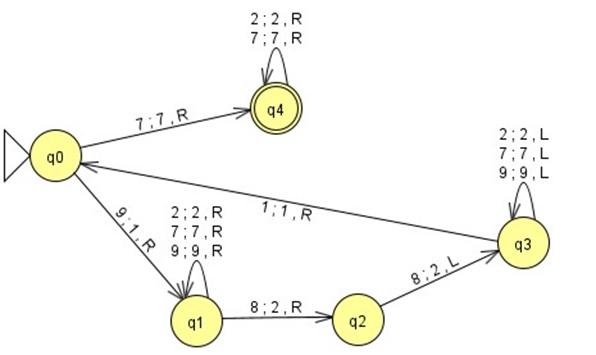
a. What is L(M₁)? Explain your answer. Show some examples of strings accepted and rejected to justify your answer. You must show at least one accepted string of length at least 6, and at least one rejected string of length at least 6. (4 marks)

b. Consider the machines M₂ and M₃, where M₂ is obtained from M₁ by adding the first transition below, and M₃ is obtained from M₁ by adding both transitions below. What are L(M₂) and L(M₃)? How do these compare to L(M₁)?

Explain your answer. (4 marks)

State     Input     Output     Direction      New State

q₀           7          1          R          q₁ q₀         9          9          R         q₄

c. Consider the language L = {w|w ∈ {a,b,c}^∗,n_a(w) = n_b(w) = n_c(w)}. Construct a Turing machine M₄ such that L(M₄) = L. (4 marks)

d. Is M₄ deterministic? Explain your answer. (2 marks)

e. Consider the language L. Will M₄ be helpful in constructing a machine for this language? Explain your answer. (3 marks)

F. Universality (12 marks)

Universal Turing machines are often discussed, but are rarely explicitly defined. This question requires you to report on one of the following topics. You should choose the one that you find most interesting. Some pointers and resources for each topic will be made available on Canvas.

This will form part 1 of an investigation; you will be able to build on and extend on this topic (or explore a different one if you wish) in Assignment 2.

Two-dimensional Turing machines

Small universal Turing machines

Notable universal Turine machines

Some more detail on each of these is below. Whichever topic you choose, you are expected to write around 800-1000 words (approximately 4 or 5 paragraphs).

You may also propose an alternative topic of your choice if you wish. In particular, anyone wishing to write a creative story involving a Turing machine of some kind is strongly encouraged to do so. However, for any alternative topic or creative story, please seek approval from the lecturer before commencing work on it.

Two-dimensional Turing machines

Turing machines were conceived in a less visual era. Whilst in principle the restriction to a one-dimensional tape does not reduce the scope of programs that can be written, there is a modern reason why a two-dimensional version is much more interesting: the predominance of the computer monitor as an output device. In particular, in the modern computing environment, there is every reason to consider abstract computations which use images as basic symbols, rather than numerals or similar strings (which, for all their mathematical properties, are visually rather prosaic). There are several varieties of two-dimensional such machines that have some rather curious properties, such as Langton’s ant, Turmites and Paterson’s worms.

Small universal Turing machines Universal Turing machines are often rather large. In 2007, a competition was held to determine whether or not a given 2-state 3-symbol machine was universal or not. The question was settled in the affirmative, with the winner of a US$25,000 prize being a 20-year-old undergraduate. The quest for small universal machines continues, as there is some issue about the precise definition of universality used in the competition. You can write a report about the competition itself, or on aspects of the quest for small universal Turing machines. Perhaps pick a side in the debate (i.e. was the winning machine actually universal? Should the definition of universality be changed as a result?) and argue for it. Or argue for both sides and come to your own conclusion.

Notable universal Turing machines It is remarkably difficult to find ’good’ explicit examples of Turing machines. Some well-known examples include Turing’s original machine, and machines built in particular ways by Minsky, Colmerauer and Wolfram. For example, Colmerauer built his machine as a means of teaching assembly language programming (!!), and intended it to be programmable. Minsky, on the other hand, derived his machine from principles of tag systems, and while it is certainly universal, it is harder to imagine programming it. There is also a relatively recent universal machine in two dimensions constructed by Dershowitz and Dowek, for which a Java implementation is available via Github.

G. The Platypus game. For this task you will need to be familiar with the

Platypus game. (27 marks)

You have been allocated a number of machines, based on your student number.

a. Play a tournament amongst your entire list of machines. There is SWI-Prolog code available for you to do this in Canvas. The main thing you need to do is to use your particular list of machines for the tournament. You should report your results as follows.

i. Report the top 10 machines performance, ranked in ’football’ order, ie by number of wins, and if the wins are equal, by the ratio of points score for to points scored against. You should include both the tournament.csv file generated by the software in your submission, as well as include a table in your PDF file with the top 10 according to this ranking. (2 marks)

ii. Examine your top 10 machines. Are they any key similarities or differences between them? (2 marks)

iii. How does your top 10 change if the ranking is based on overall points for, rather than as above? (2 marks)

iv. Were there any machines without a win? (1 mark)

v. Suggest at least one way in which the game rules can be changed which would alter the outcome of the tournament. Keep in mind that each tournament typically involves thousands of games, so any such change must not require input from the user during the game. (3 marks)

b. Time how long it takes your tournament to run. Record that time along with the basics of the machine on which it was run. For example, “My tournament involved 42,132 matches which took 156.5 seconds on a Windows 10 desktop with an Intel i7 processor and 16GB of RAM.” (3 marks)

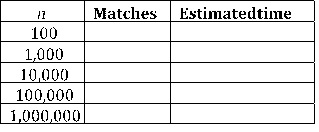
c. A tournament of this form involving n teams requires n(n + 1)/2 matches.^[1]Use your time above to calculate the average time it takes for a match on your machine, and use this value to calculate long it would take to run a tournament for 100, 1,000, 10,000, 100,000, and 1,000,000 matches. Present your results in the form of a calculation and a table of the form below. (3 marks)

d. Calculate the largest Platypus tournament you can play on your machine in 4 hours, ie 4 × 60 × 60 = 14,400 seconds. Use the value calculated above for how long it takes you to play a match. (2 marks)

e. The Platypus game is entirely deterministic, and hence a little boring as entertainment. Suggest at least two ways in which the game can be extended to increase player involvement in the game. (4 marks)

f. As discussed in lectures, some variations of the Platypus game seem appropriate. Your tasks is to rerun your tournament with your allocated machines, with different parameters, and to compare the results. You should include at least the variations below (and more if you wish). The code to do all this will be provided.

For each of the variations above, you should report the following results.

Time taken

Top 10 machines

Number of wins

Number of draws

Number of winless machines

Report your results in a table like this.

You should identify your top ten machines by the overall number, ie in the range 1 to 268,435,456.       (5 marks)