CPSC 2190

1. Translate the given English sentence into a compound proposition using logical operators and the letters b,c,h as follows:

b : The bus is on time.
c : I catch the bus.
h : I leave home early.

• (2 points) I will catch the bus if I leave home early or the bus is late.
• (2 points) If missing the bus implies I left home late, then catching the bus implies I left home early.

2. Translate the given English sentence into predicate logic using logical operators, quantifiers, and the predicates C,H,L as follows:

C(x) : x is a cute kitten.

H(x) : x is a human.

L(x,y) : x loves y.

• (2 points) No human is a cute kitten.
• (2 points) Every cute kitten loves some human.

3. (4 points) Calculate the following sum:
   
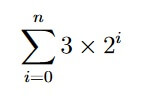
4. (4 points) For n ∈ Z+, let the set of proper factors of n be defined as

F_n := {k ∈ Z+ | k < n and n = ak for some a ∈ Z+}

For example, F₁₂ = {1,2,3,4,6}.

Prove or disprove the following statement: There exists an integer n such that

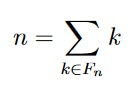
5. (4 points) You are on an island where every person is either a knight or a knave. Knights always tell the truth and knaves always lie. You encounter Alaric and Benjin. Alaric says “Benjin is a knight” and Benjin says “Either I am a knave or Alaric is a knave, but not both”. What can you conclude about the identities of Alaric and Benjin? Show your work.
6. (6 points) Prove that
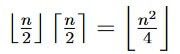
7. Consider the function

g : A → B

x 7→ 3x² − 6

where A and B are subsets of R.

• (2 points) If A = R, and B = R, is g injective (one-to-one)? Justify your answer.
• (2 points) If A = R, choose a codomain B ⊆ R so that g is surjective (onto). Justify your choice of B.
• (2 points) Let S = [0,1]. What is g(S)?

8. (6 points) Use the definition of even/odd numbers to prove that x is even if and only if 3x + 2 is even.

9. (6 points) Find the solution (closed form formula of a_n) to this recurrence relation with the given initial condition: a_n = a_n−1 − 2n, a₀ = 3.

(6 points) Assume that √21 is irrational, prove that √3 + √7 is irrational.