CS 136 Assignment 5

CS 136 - Spring 2020 - Assignment 5

• Before every assignment, make sure you read the updated preamble.
• Monitor the OFFICIAL A5 Piazza Post for any corrections, updates, or frequently asked questions.
• The assignment files are available here (they are also provided in Seashell).
• The questions are listed in (approximate) course chronological order, not necessarily in order of their difficulty or the amount of effort required.

LANGUAGE FEATURES

• In this assignment, you may only use the C features covered in class up to Section 06.
• To avoid any possible issues with stack overflow you may not use recursion.
• You may not use read_int or read_char to read input, but you may use scanf and read_symbol.
• No int in any of the questions or your tests can exceed +/- 2,147,483,647. None of our private tests will intentionally cause an integer overflow.
• We will no longer provide you with the cs136-library. Instead, we offer a limited version called cs136-trace. This library contains the tracing-tools as well as the symbol tools. It does not include C libraries anymore. From now on, you are responsible for including assert.h, limits.h, stdbool.h, stdio.h, and stdlib.h as required by your program.

Question 1: Sequence

Recall from Section 06 that a sequence is a Collection ADT that can store an arbitrary number of items. The picture below illustrates some of the behavior of a sequence ADT. Please note how adding (green items) can shift some existing items (red) to the right, while others remain at their index (gray); likewise, removing items can shift some existing items (yellow) to the left, while again others remain at their index (gray).

We are not yet at the point where we can write our own complete ADTs in C. However, we can now use an ADT as a client.

We have provided an implementation of a sequence ADT that can store integers. The interface for the ADT is provided in sequence.h and it contains all the standard functions one would expect from a sequence ADT.

GOLD QUESTION (no collaboration allowed)

You are required to write a module sequence-tools that provides functions for working with sequences:

• sequence_read(seq) reads integers from input and stores them in seq. The order within seq is the same as the order in which the integers were read.
• sequence_map(seq, func) applies func to every item in seq. This function implements the classic higher-order function map.
• sequence_filter(seq, filter) applies filter to every value in seq. Only items for which filter returns true are kept in seq. This function implements the classic higher-order function filter.
• sequence_foldr(seq, func, base) folds every values in seq using func, with base as the base value of the fold. This function implements the classic higher-order function folder. Please recall the differences between foldr and foldl.
• sequence_sort(seq, comp) sorts seq using comp as predicate.

There are already several functions in the main.c that you may use to test your code. In addition, please also implement the following two predicates in main.c. The question that all sorting-predicates ask is "does a come before b?". This means that a predicate should return true if a should be sorted in front of b.

• comp_gt(a, b) sorts in decreasing order.
• comp_eo_lt(a, b) sorts all even numbers before all odd numbers; when comparing between two even or two odd numbers, the predicate sorts in increasing order.

For this question, the Marmoset basic tests ("public" tests) will be the same as in main.

Hints:

• Make sure to read the documentation for the sequence ADT in sequence.h first, so that you have a better idea of what functionality is available.
• We strongly recommend using a sorting algorithm that you have implemented in the past, such as, selection sort. We do not care about runtime complexity at the moment, so your code does not have to meet any efficiency standards. It has to terminate within the SeaShell timeout period, though. You can assume that we will not test your algorithm with more than 100 items stored in a sequence.

Question 2: Modules, Binary Arithmetic, and Integrated Circuitry

[30 marks correctness]

In this question, we will cover a whole range of computer science and electrical engineering topics. Buckle up!

On the hardware side, the foundation of every computing device is an integrated circuit. Embedded in these "microchips" are electric circuits consisting of billions of transistors, which are grouped together to form gates. (We don't expect you to read, let alone understand the links above. Nonetheless, we wanted to share them with you because they contain some really neat foundational information.) Now, these gates are important for this question because gates implement operators in Boolean algebra (which finally brings us back to a topic we are all familiar with!).

Overall, there are seven common types of gates: the three basic gates, AND, OR, and NOT, and four more complex gates, NAND (Not AND), NOR (Not OR), XOR (eXclusive OR), and XNOR (eXclusive Not OR). We call the last four gates "complex" because they can be expressed using a combination of the three basic gates.

Once we can simulate gates and their Boolean algebra, we can combine them together to implement integer algebra. We will focus on integer addition in this assignment question. To add integers, we first need two basic adders, a half-adder, and a full-adder. A half-adder takes two-bit (or Boolean values) a and b as input and calculates their sum, e.g., a: 0 + b: 0 => sum: 0 and a: 0 + b: 1 => sum: 1. In addition it also provides a so-called carry value, which indicates if an overflow occurred during the addition: a: 1 + b: 1 => sum: 0, carry: 1. (Here, an overflow occurred because 1 + 1 = 2, or 1 + 1 = 10 in binary—remember that sum only has one single bit.)

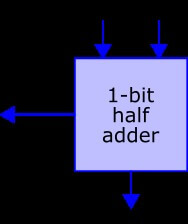
A full-adder is an extension to the half-adder in that it accepts a carry-value (c_in) as input. Like the half-adder, it also provides a carry value as output (c_out) in case that an overflow occurs: a: 0 + b: 0 + c_in: 1 => sum: 1, c_out: 0 and a: 1 + b: 1 + c_in: 1 => sum: 1, c_out: 1.

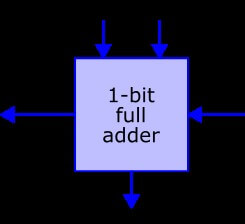
Even a full-adder can only compute the sum of (two) 1-bit integers. Since the full-adder, however, allows for carry input as well as carry output, we can now chain multiple full-adders together. This will allow us to add integers of arbitrary bit count. (Remember: int in SeaShell are made of 4 bytes = 32 bits.) There are multiple different implementations for complex adders; we will simulate a so-called ripple-carry adder since it is fairly straight-forward to implement. The figure below illustrates how we can combine four full-adders to add two 4-bit integers (a and b) together. The result is another 4-bit number (sum) as well as a final overflow flag (c_out on the very left); the initial c_in on the very right is normally set to 0. The suffixes _0 through _3 signify the bits within the 4-bit number: _0 is the least significant bit, _3 the most significant.

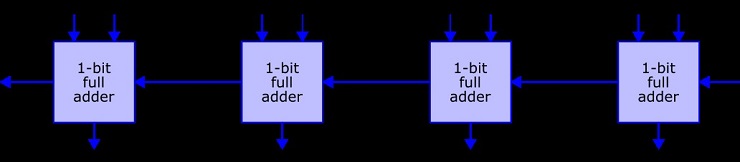
Let a be 11 (1011 in binary), b be 3 (0011 in binary), and c_in be 0. The result of this input would be sum as 14 (1110 in binary) and overflow as false:

The goal of this question is threefold: simulating gates, the (hardware) building blocks of Boolean algebra; simulating basic adders, which use gates to perform addition of binary values, i.e., TRUE and FALSE; and simulating complex adders, which allows us to perform addition on integers. In addition, we will practice the use of modules since the implementation of binary values, gates, and adders are split between multiple libraries.

For your convenience, we have already implemented the binary library. This module contains a struct binary, which stores the binary representation of an integer. It furthermore offers three functions: binary_make for creating a struct binary from an int, binary_print for printing binary and decimal representations of a struct binary (this can be useful for I/O-testing), and binary_to_decimal for converting a binary number back into its decimal representation (this can be useful for assertion-based testing). Please refer to binary.h for more information. Please be aware that strict binary is quite limited in that it can only store non-negative integers up to and including 2^4-1 = 15. Please don't hesitate to also explore the actual implementation in binary.c.

BLACK QUESTIONS (moderate collaboration allowed)

1. [q2a-gates] Implement the module boolean. This module contains the three basic gates, AND, OR, and NOT, and four more complex gates, NAND, NOR, XOR, and XNOR.

You may not include stdbool.h in your solution since the goal of this question is to write your own Boolean library. This means that you cannot use the type bool or the values true and false. Instead, you have to use the type BOOL and the values TRUE and FALSE as defined in boolean.h.

You also may not use any built-in logical operators, i.e., &&, ||, and !. Instead, you should use arithmetic and relational operators (for example, +, *, <, !=, and so on) to achieve the same behavior.

GOLD QUESTIONS (no collaboration allowed)

1. [q2b-adders] Implement the module adders. This module contains two basic adders, a half-adder, and a full-adder as well as a "nibble adder". A nibble is a, somehow colloquial, term for a half-byte or four bits. A "nibble adder" is therefore simply a 4-bit ripple-carry adder; the video above shows how such an adder might work.

[5 BONUS marks]

1. [q2c-arc-adder] Implement the module arc-adder. This module implements a general ripple-carry adder, i.e., an adder that can process binary numbers of arbitrary length.

The struct binary in the binary-module in this question now supports up to 6 bit. Your code, however, should still work for an arbitrary number of fields in struct binary. We will use strict binary with more fields in our private tests.

[0 BONUS marks]

This bonus question is worth 0 marks! Only attempt it if you have some spare time and are curious about integrated circuit design.

1. [q2d-multiplier] Implement the module parallel-multiplier. This module simulates a parallel binary multiplier. Your implementation only has to support binary numbers up to four bits in length as input.

For all four sub-questions above, the Marmoset basic tests ("public" tests) will be the same as in main.

Question 3: Fun with Stacks

[20 marks correctness]

BLACK QUESTION (moderate collaboration allowed)

1. [q3a-stackin-letters] Write a program that reads in characters from input, and prints them in their original order and then in reverse order.

GOLD QUESTION (no collaboration allowed)

1. [q3b-stackin-doubles] Write a program that reads in characters from input, and prints them in their original order, then in reverse order, then in their original order again, and then finally one more time in reverse order.

As you probably have realized by now, compilers tend to be quite particular about the syntax of your source code: the slightest error and the C-compiler will reject your code with a more or less helpful error message. One of the syntax-related errors that occur quite often are mismatching parenthesis ( ), brackets [ ], and braces { } (we will call them "groupers" from here on; there is no proper collective noun, so we just made the term "groupers" up). Since the C99 standard is quite complex, we will simplify our syntax a little bit into our new "CS136"-standard. For us, a C-program is syntactically correct if there is a closing grouper for each opening one. For example, ((a > b) && (!(a < c))) is syntactically correct, ((a > b && (!(a < c))) is not, due to a missing ). In addition, groupers have to be balanced, i.e., the inner grouper has to be closed before an outer grouper. For example, if (a > b[i]) { return 0; } is syntactically correct, if (a > b[i)] ( return {a + 1); } is not. Last, this example highlights some differences between C99 and C136: if [a > b{i}] ( return 0([{10}]); ) has correct CS136-syntax, but is (obviously) not correct C99 code.

1. [q4c-syntax-check] Write a program that reads in a text from the input and returns true if the text adheres to the CS136-syntax, and false otherwise.

For all three sub-questions above, the Marmoset basic tests ("public" tests) will use the simple. expect test files provided.

Question 4: Style

[20 marks style]

BLACK QUESTION (moderate collaboration allowed)

You do not need to do anything for this question. By having this question, we want to let you know that one or more of the questions on this assignment will be hand-marked for coding style and the quality of your tests. We are not stating which question(s) because you should use proper style and testing on all questions.