Algebra Equations, formulae and Identities

to be able to recognise when two equations are equivalent

to be able to generate equivalent equations

to be able to explain why two equations are equivalent

to have strategies to solve equations such as 75 + 2t = 100 2t

to be able to draw a linear graph from an equation given explicitly, such as y = 2x 1, or implicitly, such as x + 2y = 8

to be able to generate the equation of a line through a given point

to be able to solve a pair of simultaneous equations graphically

ALGEBRA 1 Teaching content and approaches

Phase A: Equivalent equations

The aim of this phase is for pupils to recognise and generate equivalent equations so they are not daunted by equations that look difficult. Instead, they generate an equivalent equation that is easier to solve.

Starter or first lesson give pairs of pupils a set of equations to sort into those that they can easily solve and those that are more difficult. Store the results of this sort to refer to later when pupils are asked to consider which equations are equivalent and therefore can be solved more easily than they thought.

‘Clouding the picture’ is a rich activity that engages pairs of pupils in manipulating algebraic equations in a systematic way. It is important to start with equations involving two variables, such as 2x + y = 5, so that pupils work with equivalent equations rather than rushing to a solution. Start the task by asking what is the same and what is different about two equivalent equations such as 2x + y = 5 and 2x + y + 1 = 6. Pairs produce diagrams that illustrate links between equations by organising branches and generalising what is happening along each branch.

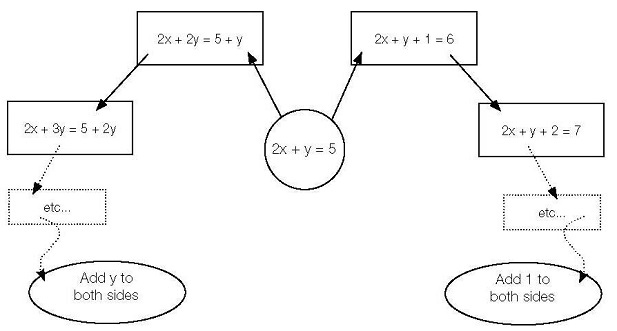
Draw out the purpose of the activity, which is that they can see how to generate equivalent forms that help them to solve an equation. Finally, repeat for an equation in one variable and ask which forms are easy to solve and which are hard. Refer back to the starter task.

Phase B: Linear relationships

Before starting this phase of the unit review substituting into equations and formulae. Pairs to use mini-whiteboards in the starter activity. Ask questions such as, ‘In the equation y = 2x + 1, if x = 3 what is the value of y?’

The rich activity involves classifying cards showing the different ways of representing linear relationships, e.g. a table of values, words, algebraic equation, coordinate graph.

Provide pairs or threes with cards to sort freely, then take feedback. If at least some feedback does not include ‘equivalence’, i.e. cards that show the same linear relationship, then guide the discussion in that direction.

Pupils continue to work on linear relationships, using textbook exercises. Pupils work in pairs, one using the textbook and giving an instruction, such as:

draw a graph of y = 2x 3.

find an equation that could go through the point (0, 3).

The other pupil uses a square grid whiteboard to draw the graph, then both check it with the textbook solution. Both sketch the correct graph in their exercise books, adding:

an equation of the line they have drawn;

several equivalent equations that would also represent the line they have drawn.

Encourage pairs to deal with equations written implicitly, as well as explicitly, and reflect on what caused problems and why. For a few examples, each pair should note what the equation could mean in a real-life application.

Phase C: Simultaneous equations

Build on from phase B by asking each pupil to draw a line going through a given point. Collect the equations of all the lines that are generated and check whether any are equivalent. Sketch two different lines on an omnigraph and ask:

What is special about the point of intersection?

Is this the only point that is on both lines and has exactly the same coordinates?

What does this mean? Can anyone give a real-life interpretation?

Repeat for another pair of equations. Try to input a pair of equivalent equations; ask pupils to predict what will happen and to explain why.

Use textbook exercise to turn this task around given two equations, sketch them and find the approximate coordinates of the point of intersection. Reinforce that all points on a line are solutions to one equation and the point where two linear graphs intersect must be the solution to both equations.

Do not teach the algebraic method of solving equations at this stage as this will be covered in the autumn term of Year 11. Where possible, apply to real-life situations, e.g. comparing mobile phone tariffs.