MATH221 Business Mathematics II
Group Project
Part 1:
For the function
- Find the equations of the two tangent lines at the points x = 0 and x = 1, respectively.
- Find the intersection point of the two tangent lines, if any.
Solution:
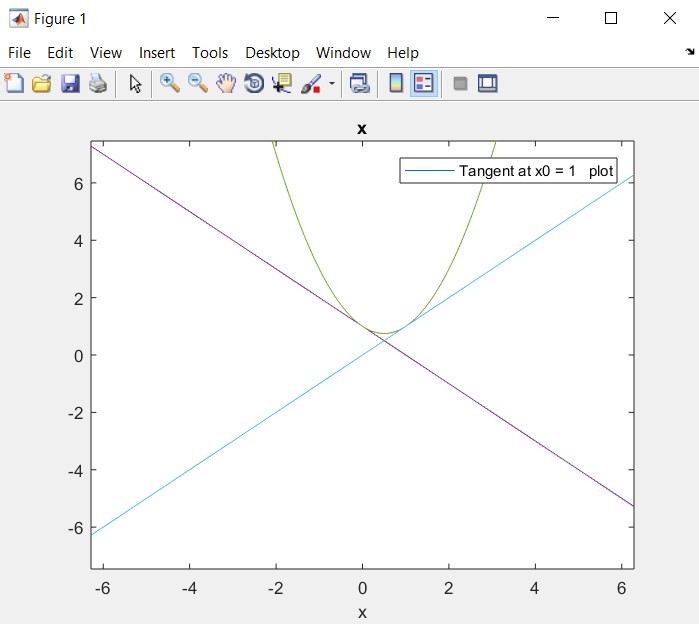
To simulate the function f(x) in MATLAB following program is executed to plot and determine the tangent.


a)
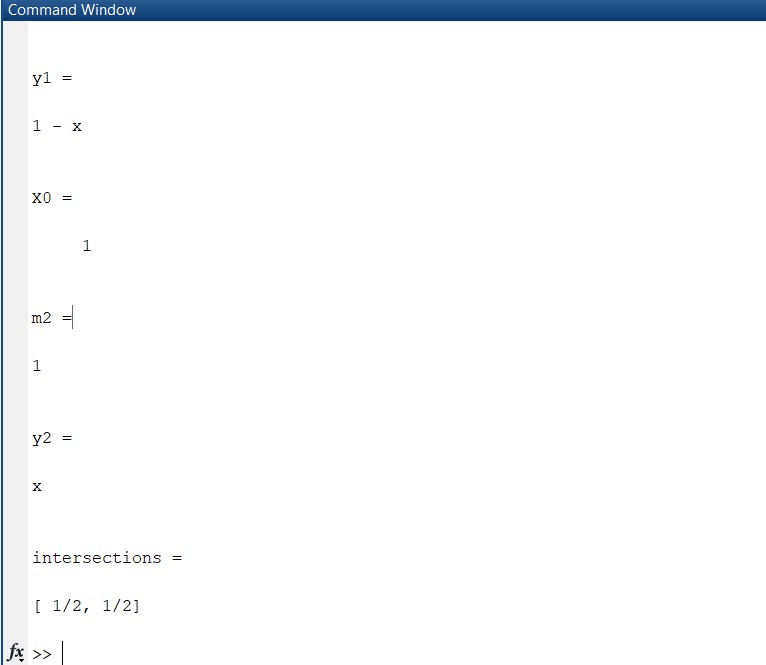
The equation of tangent line is,
y = 1 – x, for x = 0,
y = x, for x = 1
- b) The intersection point of the two tangent lines is ( ½ , ½)
Part 2:
Consider the following demand, supply and total cost functions:
Demand function:
Supply function:
- Determine the price and quantity at the equilibrium.
- Calculate the consumer surplus.
- Calculate the producer surplus.
Solution:
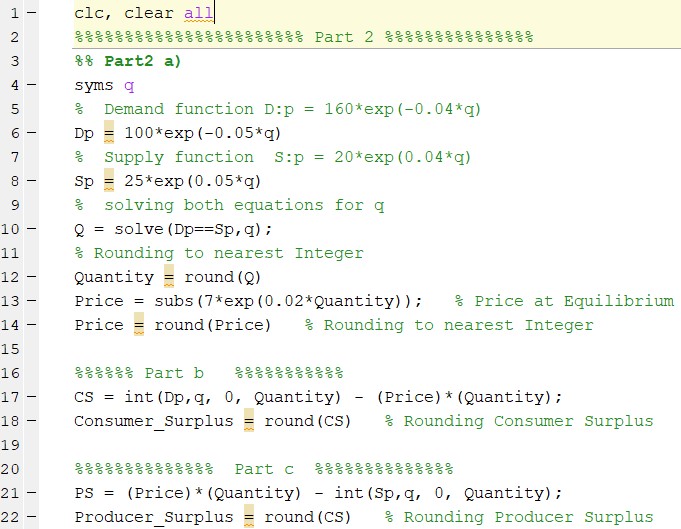
- Determine the price and quantity at the equilibrium.
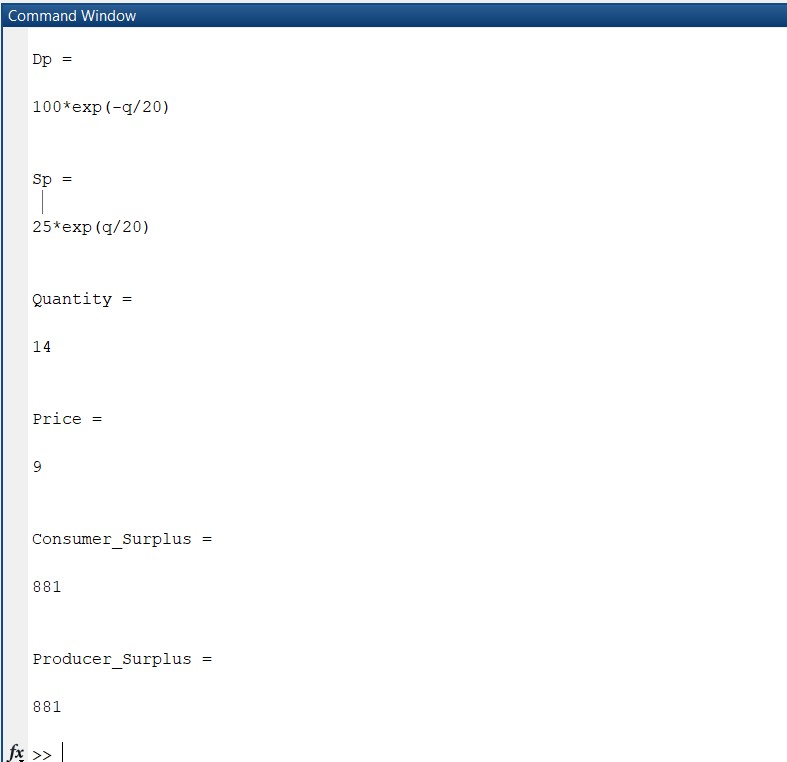
at equilibrium Demand function = Supply function.
Price is 9 units and quantity is 14 units.
- Calculate the consumer surplus.
We have to find the area under demand curve to get Consumer Surplus for this we need to integrate Demand curev w r t Quantity from q = 0 to Equilibrium
Quantity and then subtract area (Price)x(Quantity) at equilibrium
The consumer surplus is 881.
- Calculate the producer surplus.
We have to find the area under demand curve to get Producer Surplus for this we need to integrate Supply curve w r t Quantity from q = 0 to Equilibrium
Quantity and then subtract it from area (Price)x(Quantity) at equilibrium
The Producer surplus is 881.
Part 3
If the function is subject to the constrain
- Use Lagrangian multipliers method to find the critical points of the function .
- Plot the function in the 3-D graph in MATLAB.
- Using Matlab function “fmincon”, find the maximum and minimum of the function .
Solution:

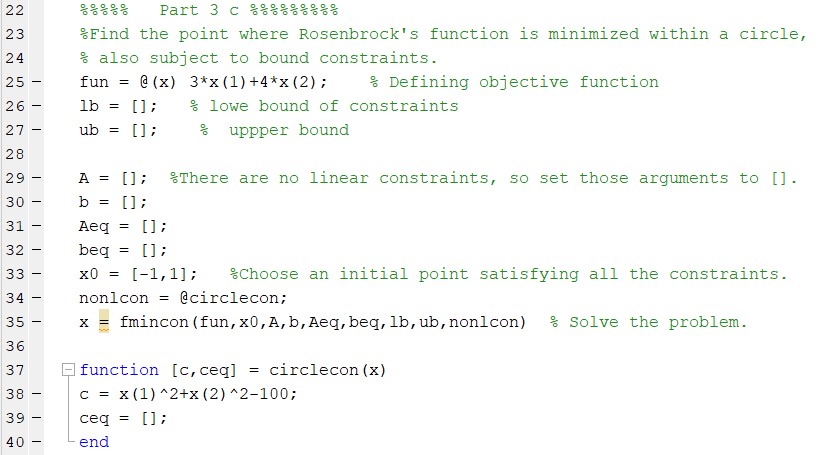
- Use Lagrangian multipliers method to find the critical points of the function .
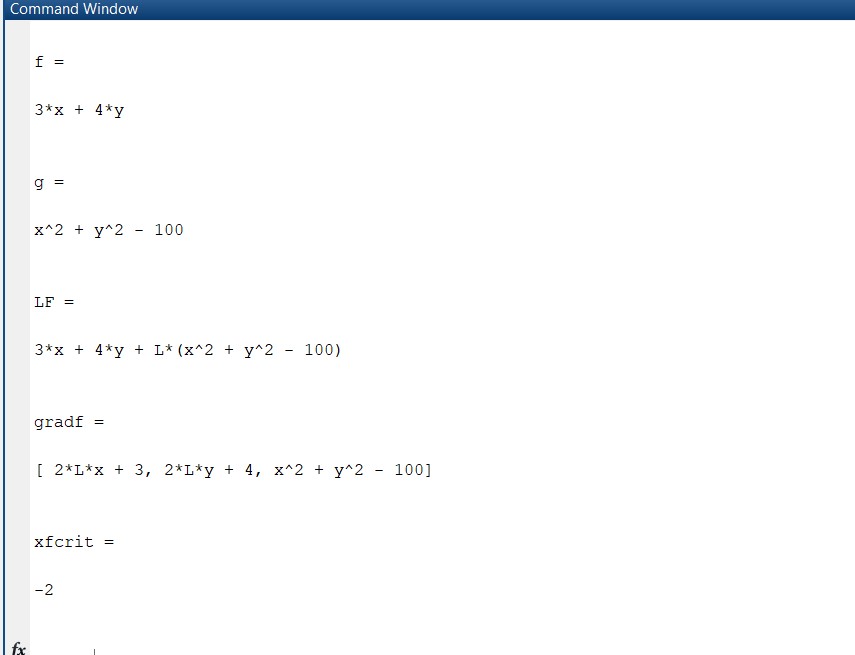
The critical point is -3 for the function.
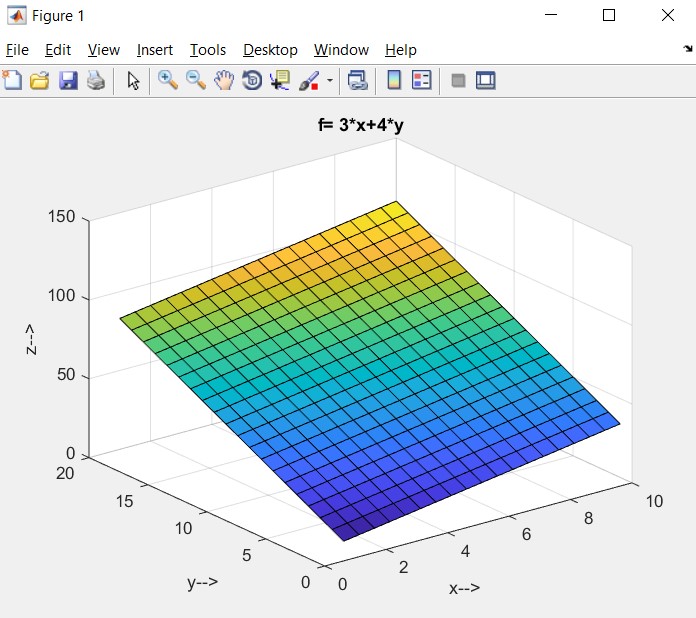
- Plot the function in the 3-D graph in MATLAB.
- Using Matlab function “fmincon”, find the maximum and minimum of the function .’
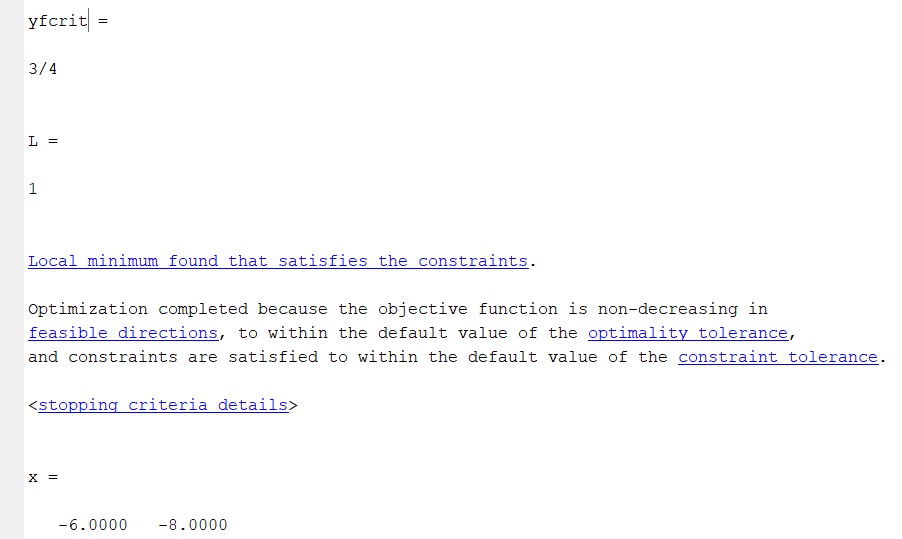
The maximum is -6.0 and minimum is -8.0 of the function.
Part 4
Suppose that a restaurant has certain fixed costs per month of $5000. The fixed costs could be interpreted as rent, insurance etc. The marginal cost function of the restaurant is given by:
dc/dq = [0.8 (0.5q2 - 25q ) + 0.4]
wherec is the total cost in dollars of producing q units of good per week.
- Find the cost of producing units, units and units per week.
- What do you notice? Explain your results.
Solution:
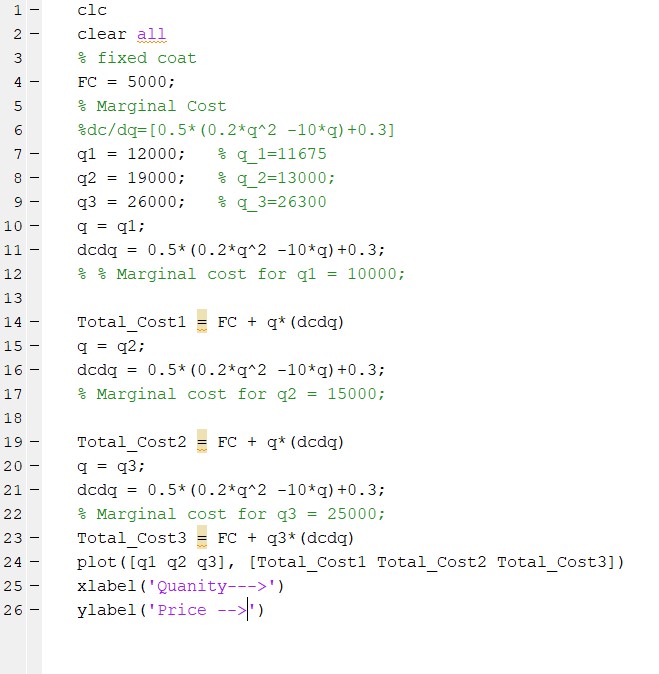
- Find the cost of producing units, units and units per week.
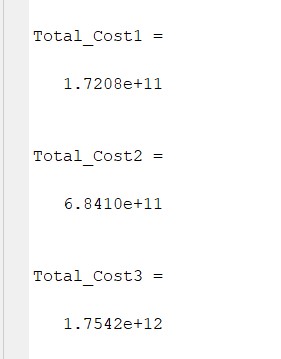
The total cost of producing q1 is 1.7208 x 1011, q2 is 6.8410 x 1011 and q3 is 1.7542 x 1011
- What do you notice? Explain your results.
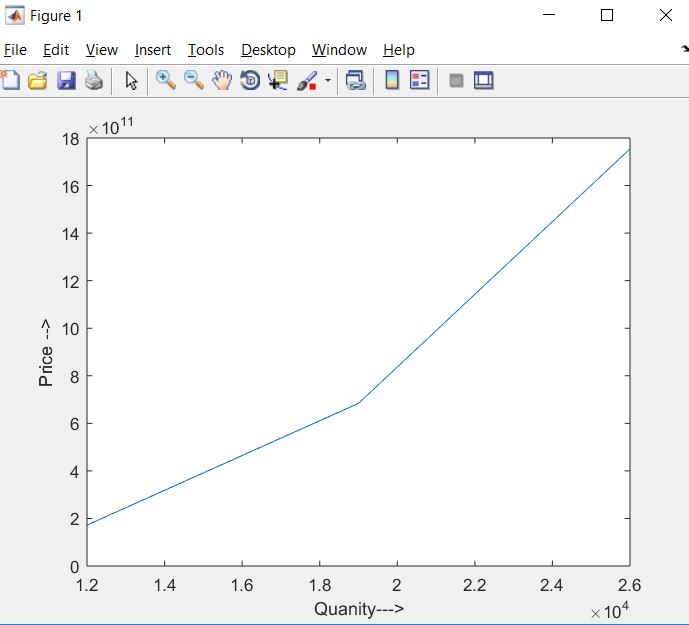
Total cost is increasing with the increase in the quantity. As it is observed from the graph of the function plotted between price and quantity.
|
Group |
Part 1 |
Part 2 |
Part 3 |
Part 4 |
|
2 |
f(x)= x2-x+1 |
D: p=100 e-0.05q S: p= 25 e0.05q | f(x,y)= 4x+3y g(x,y)=x2+y2=100 | dc/dq=[0.8(0.5q^2-25q)+0.4] s q1=12000;q2=19000;q3=26000 |
Buy MATH221 Business Mathematics II Assignment Answers Online
Talk to our expert to get the help with MATH221 Business Mathematics II Assignment to complete your assessment on time and boost your grades now
The main aim/motive of the management assignment help services is to get connect with a greater number of students, and effectively help, and support them in getting completing their assignments the students also get find this a wonderful opportunity where they could effectively learn more about their topics, as the experts also have the best team members with them in which all the members effectively support each other to get complete their diploma assignments. They complete the assessments of the students in an appropriate manner and deliver them back to the students before the due date of the assignment so that the students could timely submit this, and can score higher marks. The experts of the assignment help services at urgenthomework.com are so much skilled, capable, talented, and experienced in their field of programming homework help writing assignments, so, for this, they can effectively write the best economics assignment help services.
Get Online Support for MATH221 Business Mathematics II Assignment Assignment Help Online
Resources
- 24 x 7 Availability.
- Trained and Certified Experts.
- Deadline Guaranteed.
- Plagiarism Free.
- Privacy Guaranteed.
- Free download.
- Online help for all project.
- Homework Help Services
Testimonials
Urgenthomework helped me with finance homework problems and taught math portion of my course as well. Initially, I used a tutor that taught me math course I felt that as if I was not getting the help I needed. With the help of Urgenthomework, I got precisely where I was weak: Sheryl. Read More

