Number Theory Sample Homework

Prime Numbers

Prime Numbers can be described as •“Positive integers p>1 is often called a prime number which has no positive integer divisor other than itself i.e. p and 1. In other words, prime numbers are those positive integers that have only one positive divisor and it must be other than 1 (Eberl and Paulson, 2018).

• This shows that it must be a number that cannot be factorized

• For instance, the only divisor of 117 is 17 due to which 17 is a prime number. On the other hand, 24 has multiple divisors i.e. 1, 2, 3, 4, and 6 etc. (Vinogradov, 2016).
• In number theory, the primary role of a prime number is that every integer which is greater or equal to 2 i.e. n>=2 can be expressed as a prime product (Bachanan, 2018).

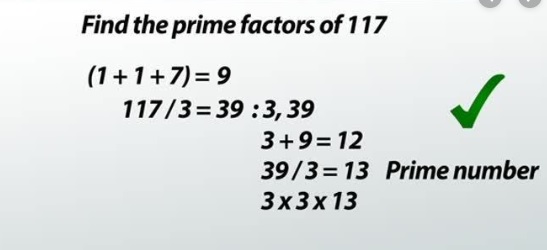
Prime Number Theorem

• Carl Friederichs Gauss was known as a great German mathematician who provide an equivalent of the prime number in 1800. Until 1896, the theorem was not approved by the committee. It was approved after the study of Charles and Jacques-Salomon Hadamard which present the same contribution (Eberl and Paulson, 2018).
• Prime number theorem can be described as the asymptotic distribution of primes that occurs among the random integers i.e zero and some other integers n.
• Approximately 1/ln(n) per cent is the probability that the integer is must be a prime number (Bachanan, 2018).

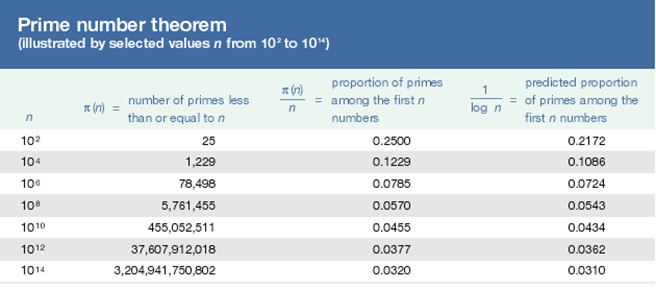
• According to Eberl and Paulson (2018), Distribution of prime number according to the asymptotic law of distribution is that:

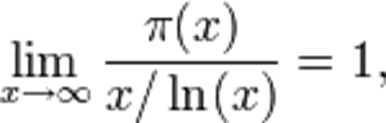
Where as,

• The prime-counting function represented by x which is used to donates the prime number that is equal to or less than x.
• X/Ln (x) is the approximation that is used to produce relative error. This error leads the function up to zero as x approaches to infinity.

Trial Division

• The easiest and simplest method to understand the integer factorization algorithms is the trial division.
• The most important thing about the trial division is that it is used to determine where n is a multiple of any integer i.e. It lies between 2 and sqrt(n) (Mauduit and Rivat, 2015).
• Through excluding even integers such as n>2 from being tested the time can be improved in an algorithm (Eberl and Paulson, 2018).
• The main problem of the trial division is that it is slow and inefficient.
• Another problem is that when the prime number is large then it is harder to find its factors (Mauduit and Rivat, 2015).
• According to the prime number theorem, prime numbers are infinite.

Mersenne Primes

Absolute Prime Number

• An absolute prime number has another name which is a permutable prime number. The main point of the absolute prime number is that it possesses two distinct digits (Vinogradov, 2016) .
• On every rearrangement and permutation, these distinct digits remain prime.
• For instance, an example of permutable is 337 and the reason behind this is that all digits are prime.

References

• Buchanan, D.M., 2018. Analytic Number Theory and the Prime Number Theorem(Doctoral dissertation, Youngstown State University).
• Eberl, M. and Paulson, L.C., 2018. The prime number theorem. Archive of Formal Proofs, 2018.
• Mauduit, C. and Rivat, J., 2015. Prime numbers along Rudin-Shapiro sequences. J. Eur. Math. Soc.(JEMS), 17(10), pp.2595-2642.
• Padmaja, C.J., Bhagavan, V.S. and Srinivas, B., 2016. RSA encryption using three Mersenne primes. Int. J. Chem. Sci, 14, pp.2273-2278.
• Stewart, I. and Tall, D., 2015. Algebraic number theory and Fermat's last theorem. Chapman and Hall/CRC.
• Vinogradov, I.M., 2016. Elements of number theory. Courier Dover Publications.