Vectors Homework Help

Vectors Homework Help and Vectors Definition

A vector is a ray with both magnitude (size) and direction. A vector is different from a scalar in that a scalar has only magnitude. For example, speed is a scalar quantity, but velocity is a vector, because it gives both speed and direction. Vectors are used to show directed quantities, and can be thought of as the motion necessary to get from one point to another. Vectors are typically written as a, or

.In two-dimensional Cartesian space, a vector has the form . A unit vector is a vector with a magnitude of 1, and is written as . Any vector can be made into a unit vector in the form , where represents the vector's magnitude.

Vectors are numbers that have both magnitude and direction. A car has a velocity of 30 m/s in the south direction is a vector. There is a magnitude describing the value and a direction describing the motion. Vectors are used to describe 2 and 3-dimensional motion.

A Vector is a geometric object that has both magnitude and direction. A Scalar on the other hand just has magnitude.

Vectors are a wonderful tool in Vectors and Maths. They have a few different components.
A vector has both a magnitude (which is usually shown through the length of the vector) and a direction (where it's pointing). Velocity, for example, is a vector. Velocity, unlike speed, has a magnitude and a direction.

The direction of a Vector can be broken up into components across your axis in both 2-dimensional and 3-dimensional space.
For instance, if a velocity vector is in 2-dimension and pointing entirely horizontal in the positive direction, it's x component would be its magnitude, and its y component would be 0. If it was at some angle between 0 and 90 degrees, it would have a positive component of both x and y that

Vectors examples
speed is a scalar: I am driving at 10 miles per hour. You know you are moving at a speed but you do not know which direction you are moving.
velocity is a vector: for example, I am driving at 10 miles per hour in the north-west direction. This is an example of a vector as we know how fast we are going and in which direction we are going.
Mathematically,
the modulus of a vector, gives you a scalar which has the same magnitude as the vector.
Also, a 2d dimensional vector(x i + y j ) means that the vector as a magnitude x in the 'i' direction and a magnitude 'y' in the j direction. The total or scalar magnitude of the vector is given as √(x² + y²).

Properties of Vectors

Mathematical objects that have both the magnitude and direction are termed as “Vectors”, which is represented like an arrow. The algebraic representation of vectors is nothing but to perform easy computations. These calculations include addition and scalar multiplication of vectors. For any vectors

, and scalar a and b , the below listed properties of vector addition and scalar multiplication holds true.

1. Commutative property of addition:

2. Associative property of addition:

3. Distributive property over vector addition:

, where α ∈ R

4. Additive identity:

5. Additive inverse:

6. Distributive property over scalar addition:

, where α , β ∈ R

7. Associative property for scalar:

, where α , β ∈ R

8. Multiplicative (scalar) identity

:

Examples of Vectors

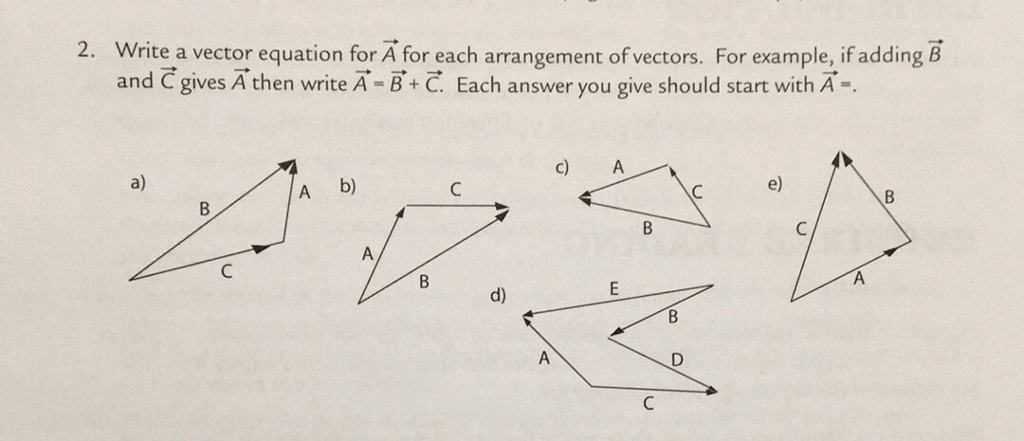
Write a vector equation for A for each arrangement of vectors. For example, if adding B and c gives A then write A -B+ C. Each answer you give should start with A- 2. C) A A b) e) d)"

(a)

          Example 3
      

A = 1.01 i + 4.75 j

B = 2.79 i + 3.77 j

So, A + B = (1.01 + 2.79) i + (4.75 + 3.77) j

A + B = 3.80 i + 8.52 j Thus, magnitude of (A+B)

= √(3.80² + 8.52²) = 9.329

Thus, R = 9.329

Angle = atan(8.52/3.80) = 65.962 deg

          Example 4
      

given vectors are (25,12,21) and (-2,2,6)

If two vectors are (x₁,x₂,x₃) and (y₁,y₂,y₃) then the distance between two vectors is given by formula

Distance = √ [(x₁ - y₁)² + (x₂ - y₂)² + (x₃ - y₃)²]

So, Distance = √ [(25-(-2)) ² + (12-2)² + (21-6)²]

= √ (729+100+225)

= √ (1054)

          Example 4: Vector addition using the component method
      

vector A = -Acos45 i + A sin 45 j

= -424.26i + 424.26 j

vector B = Bj= 500j

vector C = C cos45 i- Csin 45j

C= 282.84i - 282.84j

resultant = vector A+vector B+vector C

= (- 424.26+282.84 ) i +(424.26 + 500 -282.84 ) j

= -141.42 i + 641.42 j

magnitude of resultant = √[(-141.42)²+(641.42)²]

= 656.83 m