Geometry Triangle Assignment

1. Find the measures of the following to the nearest tenth of a degree.

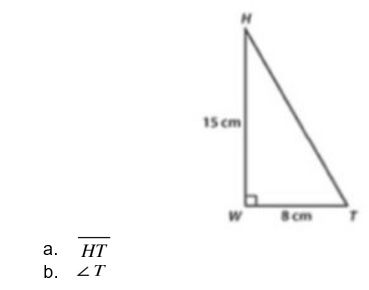
Solution

1. HT is the hypotenuse of a right angled triangle HWT thus we use Pythagoras theorem stating a² + b² = c² where c is the hypotenuse side thus Ht² = hw² +wt²

Ht² =15² + 8², HT² = 289, HT= √ (289), HT =17

1. Angle T we use cosine where cosine of angle T is adjacent side to this angle t divided by hypotenuse. Thus cos inverse of this value gives us value of <T

COS (T) = 8/17, <T = COS^-1 (8/17), <T cos-1(0.4706) = 61.9 ⁰

<T = 61.9 ⁰

2. What is the area of the given triangle?

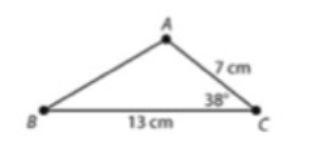
Solution

To calculate the area of the above triangle we will use the formula,

Area = ½ *a*b * sin (c) ,where a and b are any two given sides of the triangle and c is the angle between the two sides thus

Area = ½ *7*13* sin (38), 1/2*7cm*13cm*sin (38) = 28.0126 cm²

3. If X and Y are complementary angles sinX=15/17, and cosX=8/17, find each of the following :

1. tan X =

1. sin Y =

1. cos Y =

1. tsn Y =

Solution

First we put the given information into a diagram

We know Sin x = opposite side /hypotenuse side, cos x = adjacent side /hypotenuse

Thus this is a triangle with opposite side =15, adjacent side = 8 and hypotenuse =17

Also it’s a right angled triangle since 8² = 15² =17²=289

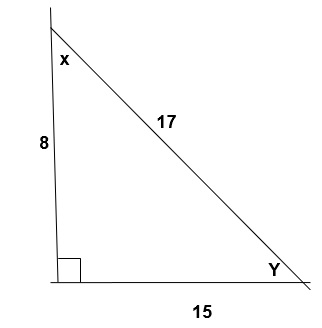
1. Tan x =opposite/ adjacent = 15/8 =1.875
2. Sin y = opposite/hypotenuse = 8/17 = 0.4706
3. Cos y= adjacent/ hypotenuse = 15/17 = 0.8824
4. Tan y = opposite/hypotenuse =8/15 = 0.5333

Buy Geometry Triangle Assignment Answers Online

Talk to our expert to get the help with Geometry Triangle Assignment to complete your assessment on time and boost your grades now

The main aim/motive of the management assignment help services is to get connect with a greater number of students, and effectively help, and support them in getting completing their assignments the students also get find this a wonderful opportunity where they could effectively learn more about their topics, as the experts also have the best team members with them in which all the members effectively support each other to get complete their diploma assignments. They complete the assessments of the students in an appropriate manner and deliver them back to the students before the due date of the assignment so that the students could timely submit this, and can score higher marks. The experts of the assignment help services at urgenthomework.com are so much skilled, capable, talented, and experienced in their field of programming homework help writing assignments, so, for this, they can effectively write the best economics assignment help services.

Get Online Support for Geometry Triangle Assignment Help Online