Math subjective test 2
Provide solution to the following questions:
- Evaluate the following: ∫xsin3xdx
This question requires integration by parts
Let u=x and dv/dx =sin (3x)
du=x dx=1
But
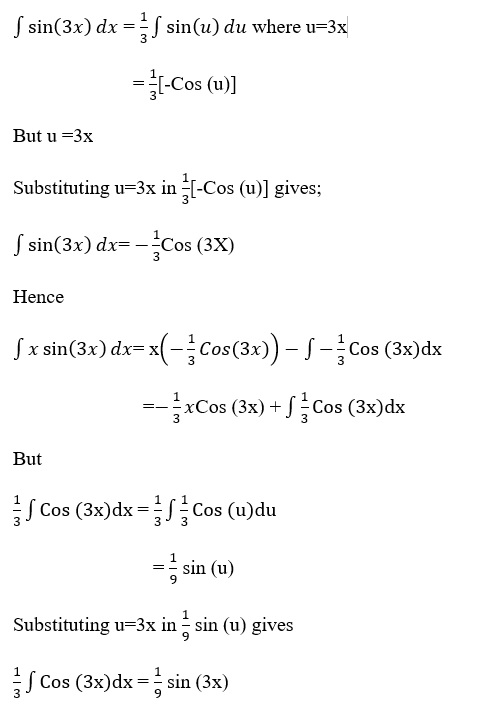

- The line y = mx + 1 is a tangent to the curve y2= 4x .Find the value of m.
Substitute y=mx+1 in =4x
= 4x
Expanding = 4x
+1+2mx-4x=0
+x(2m-4)+1=0
The tangent touches the curve at one point hence the roots are equal. Therefore, discriminant =0
-4((1) = 0
+16-16m-=0
16-16m=0
16=16m
M=1
- Solve the following differentialequation:(x2 − y2) dx + 2 xy dy = 0.
Te integrating factor of the equation is

- Solve system of linear equations, using matrix method.
x − y +2z =7
3x +4y −5z =−5
2x − y + 3z = 12

Hence
X=2
Y=1
Z= 3
Reference
Chirgwin, B., & Plumpton, C. (2016). A course of mathematics for engineers and scientists. Elkins Park: Pergamon Press/Elsevier Science.
Buy Math subjective test 2 Answers Online
Talk to our expert to get the help with Math subjective test 2 to complete your assessment on time and boost your grades now
The main aim/motive of the management assignment help services is to get connect with a greater number of students, and effectively help, and support them in getting completing their assignments the students also get find this a wonderful opportunity where they could effectively learn more about their topics, as the experts also have the best team members with them in which all the members effectively support each other to get complete their diploma assignments. They complete the assessments of the students in an appropriate manner and deliver them back to the students before the due date of the assignment so that the students could timely submit this, and can score higher marks. The experts of the assignment help services at urgenthomework.com are so much skilled, capable, talented, and experienced in their field of programming homework help writing assignments, so, for this, they can effectively write the best economics assignment help services.

