MATLAB control instrumentation
SECTION A: Instrumentation
Part A1: Sensor Selection
The last 4 digits of student id is 2684
Therefore,

The most appropriate sensor is the differential pressure sensor with the range of 0-100mBar as described by the choices above.
Part A2: Transient Response
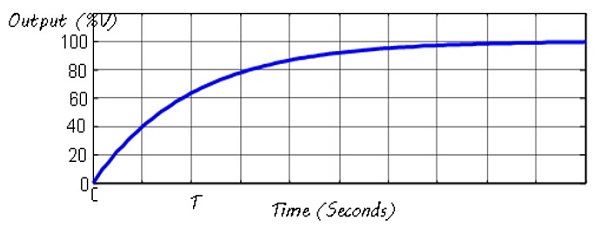
After switching the pump “on”, the step response takes T=82 s to reach 63.2% of its steady state value as shown in the figure. This indicates that the time constant of the pump is τ=82 seconds.
The rise time of the system is related to the time constant approximately by:
Tr=2.197 τ
Tr=2.197×82=180.154 s
As the pump is gradually switched on from “off” to “fully on”, the output response goes from transient state to a steady state value of 100 for large values of t. The step response, however, has no overshoot and as can be seen, the system is overdamped.
To calculate the bandwidth, we assume an oscilloscope that follows the following rule:
Bandwidth ×Rise time=0.35 Bandwidth,BW=0.35/180.154=0.00194 dB 20 logBW=0.00194 logBW=0.00194/20=0.000097 BW=100.000097=1 rad/s
Part A3: Filter Design
Using an RC filter design
Let:
C=10uF
Corner frequency is at two octaves above the bandwidth of the system at unity gain, K=1
Therefore:

SECTION B: Control
Part B1
Modelling
G(s)=Y(s)/U(s) =A/(s2+As+A.B)
The last 4 digits of student id is 2684
Therefore,
'wxyz^'=2681 A=0.9(26/99)+0.5=0.74 B=2(81/99)+1=2.64 A=0.74,B=2.64
The underdamped second order system is given by:
G(s)=0.74/(s2+0.74s+0.74(2.64))
=0.74/(s2+0.74s+1.9536)
Generally, the second-order transfer function takes the form of:
G(s)=(w02)/s2+2ζwo s+w20
Where w0 is the natural frequency, ζ is the damping ratio.
Therefore, by comparison of the 2 equations

Plotting in MATLAB
Part B2: Control
Part (i)
Finding the closed loop system transfer function
Forward path/Open loop transfer function
Y(s)/E(s) =KI/s (G(s))
=(0.74 KI)/(s(s2+0.74s+1.9536))
Closed loop transfer function

clear
clc
s=tf("s");
G=0.74/(s2+0.74*s+1.9536);
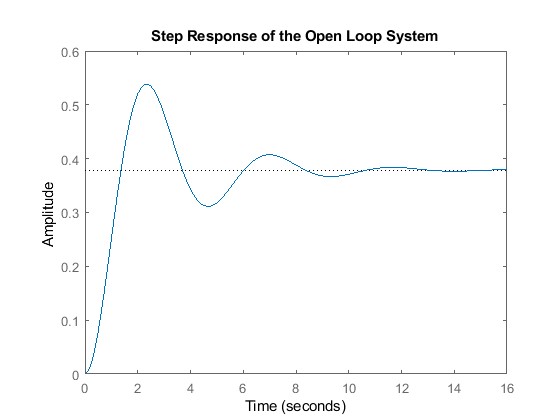
figure (1)
step(G)
title("Step Response of the Open Loop System")
Part (ii)
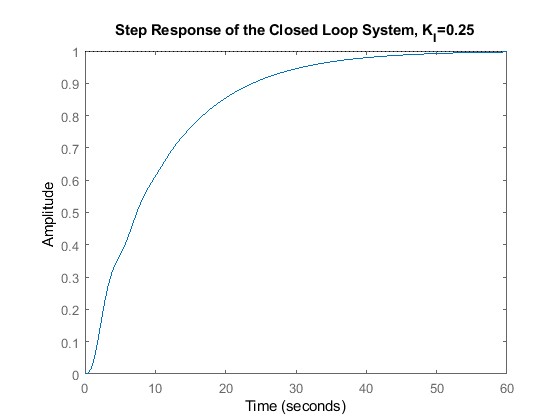
Choosing a KI of 0.25 which is in the range of , the step input response is obtained using MATLAB.
%Let Ki=0.25 since for stability 0< Ki <1.9536
Integral_Controller=0.25/s;
G1=Integral_Controller*G;
T=feedback(G1,1);
StableOrNot=isstable(T)
figure(2)
step(T)
title("Step Response of the Closed Loop System, K_I=0.25")
StableOrNot =
logical
1
Buy MATLAB control instrumentation Assignment Answers Online
Talk to our expert to get the help with MATLAB control instrumentation Assignment to complete your assessment on time and boost your grades now
The main aim/motive of the management assignment help services is to get connect with a greater number of students, and effectively help, and support them in getting completing their assignments the students also get find this a wonderful opportunity where they could effectively learn more about their topics, as the experts also have the best team members with them in which all the members effectively support each other to get complete their diploma assignments. They complete the assessments of the students in an appropriate manner and deliver them back to the students before the due date of the assignment so that the students could timely submit this, and can score higher marks. The experts of the assignment help services at urgenthomework.com are so much skilled, capable, talented, and experienced in their field of programming homework help writing assignments, so, for this, they can effectively write the best economics assignment help services.

