Periodic Functions in Real Life Situations
Periodic Functions
Periodic functions are encountered in very many aspects of our day to day lives. These areas include heartbeats in both human beings and animals, moon orbiting the earth, rotation of the earth, and oscillations of the watch clock. I will now consider another example in our day to day lives where trigonometric functions are very applicable. According to Ashour (2000) the sine and cosine functions can be used to represent the changes in temperature data all over the year. An equation that can be expended to epitomize these data is of the form: y = A cos Ø (x - C) + D, where A,B,C,D, are constants, y represents the temperature in °C and x is the months of the year from January to December.
Procedure
Generate an archetypal of the data to foretell the times during the year that a location would be amiable to visit. This possibly will be when the mean monthly temperature is above 14°C.
Month Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
°C 17.8 17.9 16.6 14.4 12.0 10.2 9.5 9.9 11.3 12.9 14.5 16.4
z
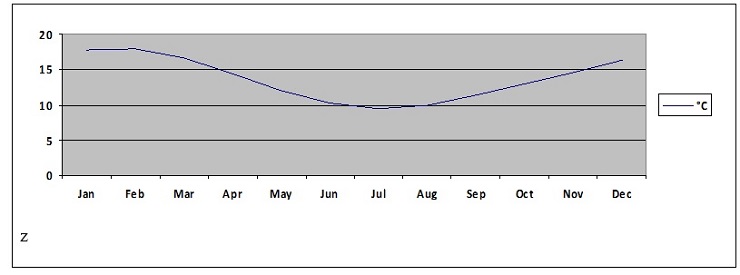
Above is a table of mean monthly temperatures at a small town x in Afghanistan from 2000-2009
Epitomize the above information on a Graph
Come up with trigonometric equation using the cosine function that best suits this situation.
Redraft the equation using the sine function.
Below is a table of mean monthly temperatures for town x for the year 2009.
Month Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
°C 17.1 17.6 15.7 15.2 13.3 11.0 10.7 10.3 12.0 13.7 13.1 17.8
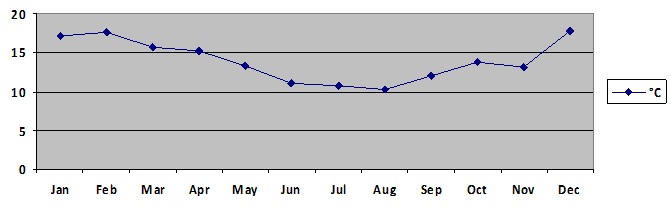
Graph this data and note down a trigonometric equation to model this data.
Solve the trigonometric equation derived resulting from the above and find when the mean temperature will be over 14°C in town x.
To represent a given real life circumstances, using trigonometry, the standard for the enduring mean is y = 4.2cos ((x - 1)π/6) + 13.7
Substitute January to December with 1 to 12.
In another discretion, form: y = 4.2sin((x + 1)π/6) + 13.7
A = amplitude = (ymax - ymin)/2
B = 2π/12
C = units turned to the right
D = ymin + amplitude = units turned up
y = 3.75cos ((x - 2)π/6) + 14.05 or
y = 3.75cos ((x - 1)π/6) + 14.05
Replace January to December with 1 to 12.
The long-term average reduces the impact of one-off, very extreme events. The climate model does not fit this data as well because of random climate variability. To find when the temperature will exceed 14°C, substitute 14 for y in the equation.
4.2cos ((x - 1)π/6) + 13.7 = 14
4.2cos ((x - 1)π/6) = 0.3
cos ((x - 1)π/6) = 0.07143
(x - 1)π/6 = 1.4993
x - 1 = 2.8635
x = 3.8635
The general solution is x = 2nπ ± 3.8635 giving 3.86 or 10.15
i.e. the temperature will be above 14°C from the end of April to early October.
References
Ashour, A. A. (2000). Mathematics for 21stCentury: Proceedings of the International Conference, Cairo: World Scientific.
Buy Periodic Functions in Real Life Situations Answers Online
Talk to our expert to get the help with Periodic Functions in Real Life Situations to complete your assessment on time and boost your grades now
The main aim/motive of the management assignment help services is to get connect with a greater number of students, and effectively help, and support them in getting completing their assignments the students also get find this a wonderful opportunity where they could effectively learn more about their topics, as the experts also have the best team members with them in which all the members effectively support each other to get complete their diploma assignments. They complete the assessments of the students in an appropriate manner and deliver them back to the students before the due date of the assignment so that the students could timely submit this, and can score higher marks. The experts of the assignment help services at urgenthomework.com are so much skilled, capable, talented, and experienced in their field of programming homework help writing assignments, so, for this, they can effectively write the best economics assignment help services.

