Probability Assignment
41) (a) A Venn diagram
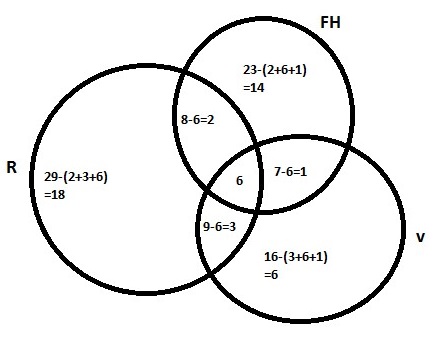
b) P(RuF) = P(R)+P(F)-P(R-F)
=29/50+23/50-8/50
=44/50
=0.88
c) 14+18+6=38
P(only one sport)
=38/50
= 0.76
d) P(Volleyball/Rugby)
=P(VuR)/P(R)
=9/29
=0.31
e) P(Field Hockey/Not Rugby)=15/21
=5/7
=0.714
35) (a) P(A’) and P(B’)
=7/100x13/100
=91/10000
(b) P(A) and P(B)
=93/100x87/100
=8091/10000
(c) At least one of the test detects steroid = 1-None shows presence of steroid
= 1-91/10000
=9909/10000
6) a) We have to fill 4 spaces. We are left with 8 numbers to choose from (1,2,3,4,5,6,8,9)
4P4*7
7*5 ways – 5P48*7.
To eliminate zero, we fix zero in the first and rearrange the remaining number in the last four spaces. Hence, 4P4*7 such cases,
The total codes = 5P4*8*7)-4P4*7
=280-28
=252 codes
- b) 3 as the third and 5 as the fifth=5!/(n-2)!
=5x4x3x2x1/(5-2)!
=120/6
=20 Codes
- c) To begin with an even number, The 1st letter can be arranged in 4! Different forms starting with the four even numbers, that is 2,4,6,8
The 2nd,3rd, 4th and 5th can be arranged in 4! Ways. Hence, number of arrangement = 4!x4!
=576codes.
- d) Begin and end with even number.
1st – 4!
5th – 4!
2nd, 4th and 5th can be arranged into 3! ways.
Hence, The total codes=4!x4!x3!
=576x6
23) Let 5 be the 1st digit. The other four digits can have either of the other 9 choices, as we have excluded 8. This gives 9^4 numbers.
Let 5 be the 2nd digit. The first digit can have either of 7 choices, excluding 5, 8 and 0. The other three digits can have any of the 9 choices. This gives 7 * 9^3 numbers.
Let 5 be the 3rd digit. The first digit can have either of 7 choices, excluding 5, 8 and 0. The 2nd digit can have 8 choices excluding 5 and 8. The other two digits can have any of the 9 choices. This gives 7 * 8 *9^2 numbers.
Let 5 be the 4th digit. The first digit can have either of 7 choices, excluding 5, 8 and 0. The 2nd and 3rd digits can have any of 8 choices. This gives 7 * 8^2*9 numbers.
Let 5 be the 5th digit. The first digit can have either of 7 choices, excluding 5, 8 and 0. The 2nd, 3rd and 4th digits can have any of 8 choices. This gives 7 * 8^3 numbers.
Hence, the total possible numbers;
= 9^4 + 7*9^3 + 7*8*9^2 + 7*8^2*9 + 7*8^3= 23816
Buy Probability Assignment Answers Online
Talk to our expert to get the help with Probability Assignment to complete your assessment on time and boost your grades now
The main aim/motive of the management assignment help services is to get connect with a greater number of students, and effectively help, and support them in getting completing their assignments the students also get find this a wonderful opportunity where they could effectively learn more about their topics, as the experts also have the best team members with them in which all the members effectively support each other to get complete their diploma assignments. They complete the assessments of the students in an appropriate manner and deliver them back to the students before the due date of the assignment so that the students could timely submit this, and can score higher marks. The experts of the assignment help services at urgenthomework.com are so much skilled, capable, talented, and experienced in their field of programming homework help writing assignments, so, for this, they can effectively write the best economics assignment help services.

