Thermodynamics Homework Help

Hire Thermodynamics Homework Help Professionals to Boost the Grades

Thermodynamics is the part of material science that manages the connections among the heat and different types of energy. Specifically, it depicts how thermal energy is changed over to and from different types of energy and how it influences matter.

Heat energy can be moved to start with one body then onto the next or between a body and the earth by three distinct methods: conduction, convection, and radiation. Conduction is the exchange of heat energy through a strong material. Conduction between bodies happens when they are in direct contact, and particles move their energies over the interface.

The four laws of thermodynamics for Thermodynamics Assignment Help Online

The fundamental principles of thermodynamics were initially communicated in three laws. The issue, however, was that the initial three laws had just been built up and were notable. The new law the "Zeroth Law." In brief, these laws are:

The Zeroth Law states that if two bodies are in thermal equilibrium with some third body, then they are also in equilibrium with each other. This establishes temperature as a fundamental and measurable property of matter.

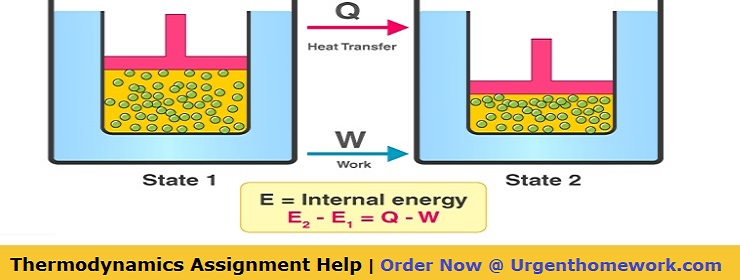
The First Law states that the total increase in the energy of a system is equal to the increase in thermal energy plus the work done on the system. This states that heat is a form of energy and is therefore subject to the principle of conservation.

The Second Law states that heat energy cannot be transferred from a body at a lower temperature to a body at a higher temperature without the addition of energy. This is why it costs money to run an air conditioner.

The Third Law states that the entropy of a pure crystal at absolute zero is zero. As explained above, entropy is sometimes called "waste energy," i.e., the energy that is unable to do work, and since there is no heat energy whatsoever at absolute zero, there can be no waste energy

The Zeroth Law: It expresses that on the off chance that two bodies are in thermal balance with some third body, at that point they also in equilibrium with each other. This sets up the temperature as a key and quantifiable property of the issue.

The First Law: It expresses that the total increase in the energy of a framework is equivalent to the expansion of thermal energy plus the work done on the framework.

i.e Change in Internal Energy = Change in Thermal Energy + Work done

The Second Law: It states that heat energy can't be moved from a body at a lower temperature to a body at a higher temperature without the expansion of energy. This is the reason it costs cash to run a climate control system.

The Third Law: It expresses that the entropy of an unadulterated precious stone at outright zero will be zero. As clarified above, entropy is in some cases called "squander energy," i.e., energy that can't accomplish work, and since there is no warmth energy at all at supreme zero, there can be no waste vitality

Sample of Thermodynamics Homework Help Solved

a) The Generator

What are the compositions of the two phases present in the lower reservoir of the generator? Be as specific as possible. How can you tell?

b) The Bubble Pump

Why does the bubble pump itself operate at 100 °C and how can you tell? Hint: It’s not the initially-obvious answer.

c) The Condenser/Absorber

What is the operating temperature of the condenser/absorber? What are the compositions of the two liquid phases present at the bottom of the Condenser/Absorber? Be as specific as possible. How can you tell?

d) The Evaporator

What is the minimum possible operating temperature of the evaporator? How can you tell? What are the compositions of the two phases present in the evaporator if the evaporator is operating at this minimum temperature? Be as specific as possible. How can you tell?

e) That long tube...

Why is it critical for the tube in the above prototype photo that runs from the top of the generator’s lower reservoir to the top of the evaporator to be angled upwards? What condition should be met by this component of the device?

Question 2: Explaining key phenomena by chemical potential/equilibrium

a) The Generator

Why, in terms of chemical potential, does heating the ammonia/water(l) mixture enrich the vapor in ammonia and the liquid in the water? Use appropriate equation(s) to discuss this qualitatively.

b) The Condenser/Absorber

Why, in terms of equilibrium, does the falling film of water absorb the gaseous ammonia? Why does the butane condense (particularly since the operating temperature here is higher than it is in the evaporator)? Why do the two liquids form separate phases (discuss this point from the perspective of “regular solutions,” discussed in the textbook, and explain what must be true about the relative entropic and enthalpic contributions)?

c) The Evaporator

Using an appropriate expression for chemical potential, demonstrate that bubbling ammonia (g) through butane (l) at an overall pressure of 4 bar and a temperature above 265 K causes evaporation of the butane. Hint: Explain the process from the perspective of an ammonia bubble that enters the butane (l) environment.

Question 3: Ammonia-water equilibrium

a) Ideal Solution Approximation

i) Generate a plot of the vapor pressure of pure water and pure ammonia as a function of temperature over the temperature range that is relevant to the Einstein refrigerator.

ii) Generate a plot of the vapor pressures of the two components and the total vapor pressure as a function of mole fraction of ammonia assuming the mixture is an ideal solution (put this plot in a

Manipulate wrapper so that you can modify the temperature at which you are looking at this). Mathematica notes: Manipulates work much faster without built-in units.

iii) Generate a plot of the total vapor pressure as a function of mole fraction of ammonia in both the liquid phase and the gas phase (that is, the mole fraction of ammonia in the liquid phase is the x-axis of one graph, the mole fraction of ammonia in the gas phase is the x-axis of the second graph, both plotted on the same plot). Use the same type of Manipulate wrapper as you did for part (ii).

iv) The most useful version of this phase diagram has temperature vs. mole fraction at the specific operating pressure rather than pressure vs. mole fraction at a specific temperature. Unfortunately, solving the expressions you have already found for temperature is quite difficult (make sure you save before trying anything!). Nonetheless, I m going to walk you through doing it. Here is an approach that works:

First, set up a list of mole fractions running from 0 to 1 every 0.01. You will in the next few steps be finding the boiling point for these mole fractions each for the vapor mole fraction and the solution mole fraction.

In part (ii) you found an expression for the total vapor pressure at a particular temperature and solution phase mole fraction. You want to know at what temperature this vapor pressure equals the operating

temperature of the Einstein refrigerator. Unfortunately, Solve and NSolve don’t work. But FindRoot does. FindRootexpression, {var, var₀} finds a value for variable “var” where “expression” equals zero, and it starts its search at var = var₀. So you can solve an equation using FindRoot by simply taking the left-hand side of the equation minus the right-hand side, and using FindRoot. Use this approach to find the temperatures at which the total pressure equals the vapor pressure using the expression from part (ii) for all of the mole fractions you set up as a list in the previous step. This becomes the first line in your phase diagram.

Just like the last step, find the temperatures that have vapor pressures that equal the operating pressure of the Einstein refrigerator, using the expression you found in part (iii) when using the vapor-phase mole fraction as the x-axis. This becomes the second line in your phase diagram.

You now should have some densely-spaced data points for two curves for your phase diagram. Plot them on the same plot using ListLinePlot.

b) Interpretation

i) The graphs you generated in part (a) (i) through the part (a) (iii) should beat you over the head with one significant take-home message. What is it?

ii) The final graph you generated in part (a) should look similar to the first graph for reference above. Identify any noteworthy differences between these two graphs and discuss how those differences result from the ideal solution approximation. Be specific.

Question 4: Some strange hypotheticals

a) Semi-permeable membrane

An enterprising engineer wants to improve the efficiency of the water/ammonia separation in the generator by covering the inlet to the bubble pump with a semi-permeable membrane that allows water to pass but blocks the passage of ammonia (assume such a membrane exists). How would such a change modify the operation of the refrigerator? Be quantitative in your answer, but assume ideal solution behavior where appropriate.

b) Oops!

In constructing an Einstein refrigerator, a careless graduate student used tap water instead of deionized water. Qualitatively predict the effects of the ionic contaminants on each relevant physical process in the system, and draw a conclusion about the effect this would have on the overall functioning of the refrigerator.

Topics