Binary Search Trees Homework Help
A binary search tree labels every node in a binary tree with a single key such that for any node x, as well as nodes within the left subtree of x have keys <= x and all nodes in the right subtree of x have key's >= x
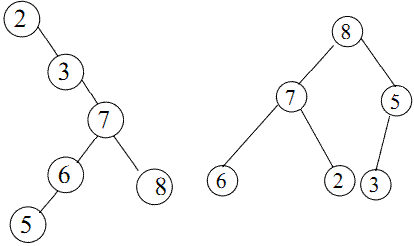
- Left : A binary search tree.
- Right : A heap but not a binary search tree.
The search tree labeling enables us to find where any key is. Start at the root- if that is not the one we want, search either left or right depending upon whether what we want is <= or >= then root.

Binary search trees store collections associated with items that may be purchased, for example integers. Binary search trees support the following standard operations.
- search(x) : determines is an item x included in the tree (and if so returns the item).
- insert(x) : adds item x to the collection stored in the tree, if it is not already there.
- delete(x) : removes item x from the collection stored in the
Data structures supporting these operations are called Dictionaries. A simple implementation is to store the items in sorted order in an array. Search(x) is simply a binary search. However, insert(x) and delete(x) are inefficient as, in general, they may require many items to be shifted.

