+1-617-874-1011 (US)Minimum Spanning Tree(MST)
- Let G = (V, E) be a simple, connected, undirected graph that is not edge-weighted.
- A spanning tree of G is a free tree (i.e., a tree with no root) with | V | - 1 edges that connects all the vertices of the graph.
- Thus a minimum spanning tree for G is a graph, T = (V’, E’) with the following properties:
V’ = V
T is connected
T is acyclic.
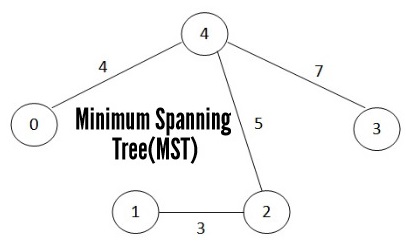
- A spanning tree is called a tree because every acyclic undirected graph can be viewed as a general, unordered tree. Because the edges are undirected, any vertex may be chosen to serve as the root of the tree.
Following are some of the areas in Minimum Spanning Tree in which we provide assignment and homework help:
Resources
24 x 7 Availability.
Trained and Certified Experts.
Deadline Guaranteed.
Plagiarism Free.
Privacy Guaranteed.
Free download.
Online help for all project.
Testimonial
Urgenthomework helped me with finance homework problems and taught math portion of my course as well. Initially, I used a tutor that taught me math course I felt that as if I was not getting the help I needed. With the help of Urgenthomework, I got precisely where I was weak:
