Complex Numbers Homework Help
Math - Complex Numbers
When mathematicians talk about {"real"} numbers, they mean any positive or negative number (decimal, fraction, irrational, etc.). So, for example, and 1 and -200.15 and pi are all real numbers. These numbers all have the property that their square is always positive. As a result, positive numbers have real numbers as square roots.
It seems a little unsatisfying to say that positive numbers, like 1 have a square root (two, actually!) but -1 doesn't have any. So, mathematicians decided to just {"imagine"} a number that was the square root of -1. They called these numbers imaginary, and defined the square root of -1 as i, the imaginary unit. Using i, we can generate the square roots of all the negative numbers: for example, the square root of -16 is sqrt (16*-1) = 4i.
These imaginary numbers are wholly different from the real numbers--there's no combination of imaginary numbers you can add together to make a real number. As a result, we can extend the number line, which all the real numbers lie on, into a second dimension, the imaginary numbers. We can draw this on graph paper, with the real numbers along one axis (like the x axis) and the imaginary numbers on the other axis (like the y axis). This two-dimensional plane of numbers is called the complex plane, and a point in this plane consists of some real component and some imaginary component: this is called a complex number. For example, 3 - 2i or 7pi + .5i are complex numbers.
Complex numbers sound, well, complicated, but they end up being a surprisingly convenient way to describe certain properties of waves and other physical phenomena.
A Complex number is of the form a +ib, where a and b are real numbers with a as real part and ib as imaginary part. All four basic mathematical operations are possible to perform with the complex numbers.
Addition of complex numbers:
First combine (group) the real parts and imaginary parts, and then add the real parts and imaginary parts separately. Finally, solution is obtained and named it as sum. For instance, if
u=a +ib and v=c+id are two complex numbers, then their sum is,
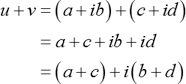
Subtraction of complex numbers:
First group the real parts and imaginary parts separately, and then perform the subtraction operation. Finally, solution is obtained, which is named as difference. For instance, the difference of two complex numbers u=a +ib and v=c+id is obtained below:
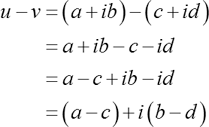
Multiplication of complex numbers:
Expand the brackets like multiplying two binomials with i 2= –1 by using the order (FOIL) given below:
1. Multiply the First terms
2. Multiply the Outside terms
3. Multiply the Inside terms
4. Multiply the Last terms
Suppose u=a +ib and v=c+id are two complex numbers, then their product is,
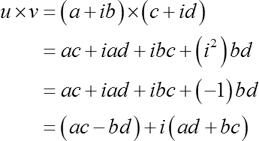
Division of complex numbers:
First, obtain the conjugate of denominator. Then, multiply the numerator and denominator by the conjugate by using multiplication of complex numbers (FOIL).
Suppose u=a +ib and v=c+id are two complex numbers, then their quotient is obtained as follows:
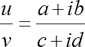
The conjugate of the denominator is c –id. Then, the quotient is,
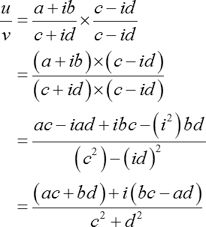
Math Tutorials
- Math - Polynomials
- Math - Series and Sequences
- Math - Dividing Polynomials
- Math - Factoring Polynomials
- Math - Solving Quadratics
- Math - Solving Inequalities
- Math - Solving Equations
- Math - Complex Numbers
- Math - Matrix
- Math - Inverse Functions
- Math - Graphing Quadratic Functions
- Math - Graphing Polynomial Functions
- Math - Functions
- Math - Exponentials and Logarithms
- Math - Cramer's Rule
- Math - Absolute Value & Inequalities

