Matrix Homework Help

Math - Matrix

Matrices are a way of organizing data similar to a table, but without a grid, basically. Matrices can be added to, subtracted from, multiplied by, and divided by each other, as well as any number. If a number is in the first row and the first column, when adding, subtracting, multiplying or dividing its matrix by another, add (etc.) it to the number in the corresponding place in the 2^nd matrix. While duplicating, increase the primary line by the main segment. This means to multiply, if your first matrix has 2 rows and 3 columns, your second must have 3 rows and 2 columns. You then multiply matching numbers in the 1st matrix's 1st row and the 2^nd matrix's 1^st column and add them up to get what goes in the 1^st spot (row 1 column 1) of the new product matrix. You then go through both rows for each column to produce 4 products in the product matrix. To divide a matrix, you rather duplicate by the backwards of a framework,

In another way a matrix is a rectangular arrangement of numbers in rows and columns. The dimension of the matrix is given by, If there are m rows and n columns, then the matrix is mxn matrix. Matrices are usually written in the parentheses or square brackets. A capital letter is always used to designate matrices.

A general form of the matrix A of dimension is given by:

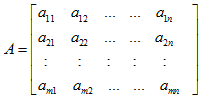
The various kinds of grid are recorded beneath:

1. Line vector lattice - A framework with a solitary line is known as column vector network.

2. Segment vector grid - A network with a solitary section is known as segment vector framework.

3. Square grid - A lattice with an equivalent number of lines and segments is known as a square framework.

4. Interminable grid - A lattice with an endless or uncountable number of lines or sections is known as a vast framework.

5. Void grid - A lattice with no line or sections is known as an unfilled network.

6. Slanting framework - A grid with all passages other the primary corner to corner is zero is known as an askew lattice.

7. Character framework - A grid with every one of the passages on the primary corner to corner as one and the rest of the sections as zero is called a personality network.

Tasks on lattices are given underneath:

1. Option of frameworks - The entirety of two grids is gotten by including the relating passages of two lattices.

2. Scalar Multiplication - Scalar increase is the duplication of a network by a fixed number.

3. Framework increase - Matrix duplication is performed by duplicating the sections of lines with the comparing passages of the segments and after that including the items.

4. Transposition - The transpose of the framework is acquired by exchanging the lines and sections.

Frameworks are generally utilized in numerous applications in everyday life. It is for the most part utilized in the fields of material science, quantum mechanics, building and complex mechanics.