Series and Sequences Homework Help

Series and Sequences

An arrangement is an arranged rundown of numbers and the whole of the provisions of a grouping is an arrangement. In a math arrangement, each term is equivalent to the past term, in addition to (or short) a steady. The steady is known as the regular distinction (d). The recipe for finding any term of a number juggling succession is

a_n = a+(n-1)d

where a is the primary term of the sequence, d is the regular distinction, and n is the quantity of the term to discover. To discover the entirety of a specific number of terms of a math arrangement use

a_n = a+(n-1)d

where Sn is the entirety of n terms, a is the primary term, and an is the nth term. A number of juggling grouping charts as focuses along a line.

Infinite Sequences and Series is a significant topic in a second-year college level integral Calculus course, as well as in the AP Calculus BC course. Many students struggle with this concept because it is much more abstract than other concepts in the Calculus sequence. Infinite series are useful for solving various types of differential equations, and in particular, the power series is very useful for approximating functions. Computer applications and scientific calculators use said approximations to evaluate different functions.

An infinite sequence is essentially just an infinite list of numbers that follow a certain pattern. Typically, a sequence is defined by some formula in terms of a variable n, and each nth term is found by plugging in the specific value of n into the equation. In general, we are concerned with the convergence or divergence of the sequence. A sequence converges, if the nth term of the sequence is approaching a finite number as n approaches infinity. A sequence diverges if the nth term of the sequence is either approaching infinity, or not approaching some finite number.

An infinite series is just the sum of an infinite sequence, so if you add up all terms of some infinite sequence, you are left with an infinite series. Infinite series are written in summation notation. Like a sequence, the series is typically written in terms of n, and we are generally concerned with the convergence or divergence of the sequence. A series converges absolutely if the sum of the series is approaching a finite number as n approaches infinity. A series diverges if the sum of the series is approaching infinity, or not approaching some finite number. A series is said to converge conditionally if it converges but does not converge absolutely. Typically, series that converge conditionally are series whose terms alternate between negative and positive.

There are multiple tests that Calculus students will learn in order to find the convergence/divergence of an infinite sequence or series, and different tests can work on the same sequence/series.

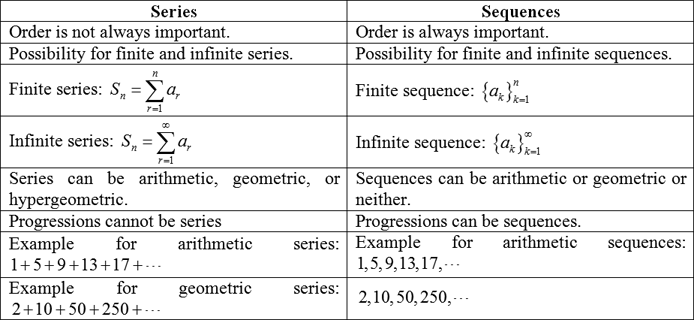
Series is the sum of the finite or infinite ordered set of terms while sequence is the collection of terms in any definite order. The comparison between the series and sequences are given below: