Dividing Polynomials Homework Help
Math- Dividing Polynomials
Dividing polynomials is one important way to be able to analyze complex expressions. If you understand how to divide polynomials, you can solve more complex problems. Dividing polynomials is interesting because it seems complex but is actually very simple to do. You take the first polynomial and leave it alone, then you take the polynomial you are dividing by and instead of putting it on the denominator and trying to solve, you flip it (1/polynomial) and multiply that expression by the first polynomial
You should know the division of polynomials in another way the Division of polynomials is a process that is much like dividing numbers.
Given two polynomials
f and g,
we ask if there is a third polynomial h
such that f=gh.
This isn't always the case, just like division of whole numbers isn't always whole.
{`
Example, if we take 7 and 3,
we have that 7=2x3+1,
`}
where 1 is the remainder of the operation. Division with natural numbers really involves the following given two numbers a and b,
there exists a number c and a number r (called the remainder),
such that r<c and a=bc+r.
This is also true in polynomials: given two polynomials f and g, we can always find two polynomials h and r such that the degree of r is less than the degree of h, and f=gh+r.
The method for finding h and r is very simple and is analogous to dividing whole numbers.
Dividing polynomials is just like long division with numbers, except you are using polynomials instead
{`
for example,
an expression with x's in it such as x^2 +2x-7
`}
You set it up the same way as normal long division.
{`
For example, let's say you're asked to divide x^2+2x-7 by x-2.
When you set up the problem, x^2+2x-7 is the numerator,
and x-2 is the denominator (and the divisor).
Write out the problem as a normal long division, with x-2 on the left, and
x^2+2x-7 on the right.
`}
Work out the problem, and you get your reminder at the bottom, and the quotient at the top.
When you write out your answer, make sure you write it as: quotient + reminder/divisor.
Example
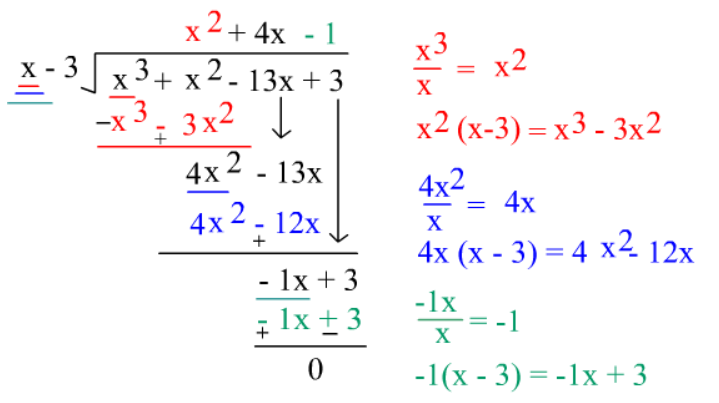
Math Tutorials
- Math - Polynomials
- Math - Series and Sequences
- Math - Dividing Polynomials
- Math - Factoring Polynomials
- Math - Solving Quadratics
- Math - Solving Inequalities
- Math - Solving Equations
- Math - Complex Numbers
- Math - Matrix
- Math - Inverse Functions
- Math - Graphing Quadratic Functions
- Math - Graphing Polynomial Functions
- Math - Functions
- Math - Exponentials and Logarithms
- Math - Cramer's Rule
- Math - Absolute Value & Inequalities

