Polynomials Homework Help

Previous Next

Polynomials

A mathematical expression contains constants, variables and non-negative integer exponents, that can be combined by using the basic mathematical expressions like addition, subtraction and multiplication but not division by a variable is called polynomial. In Greek, “Poly” means ‘many’ and in Latin “nomial” means ‘terms’. Thus, it is defined as an expression with many terms.

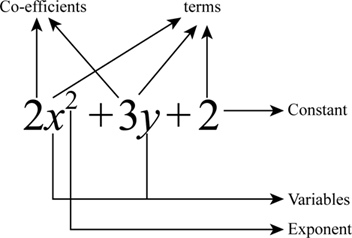
Note that, a term includes one or more variables raised to the non-negative integer power and multiplied by a constant co-efficient. The term includes only a constant is called constant term. Moreover, it is not possible to have infinite number of terms in a polynomial.

Polynomial function:

If there is only one variable involved in a polynomial, then it is named as a polynomial function. The general form of a polynomial function is as follows:

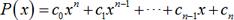
Where c0, c1,…cn-1,cn is a constants in R and n is a non-negative integer.

Note that, c0xn+c1xn-1+…+cn-1x+cn is a one-variable polynomial.

Examples:

1. Consider 2x2+3y+2. Here the number of terms is 3. Variables are x,y whose highest degree, 2. It is a polynomial.

2. Consider –4x2+5y–3+2. Here, the number of terms is 3. Variables are x,y in which y has a negative exponent. It is not a polynomial.

3. Consider
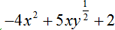
. Here, the number of terms is 3. Variables are x,y in which y has a fractional exponent. It is not a polynomial.

4. Consider
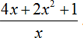
. Here, the number of terms is 3. Variables are x,y with one variable is a division of another variable. It is not a polynomial.

Types of polynomial: