Solving Quadratics Homework Help
Example of Solving Quadratics
Solving Quadratics The quadratic formula is a formula created to solve for quadratic equations. It takes the three numbers, the numerical coefficients, to use the quadratic equation. Once the numbers are plugged into the equation, the answer is simplified to find the variable.
Sometimes a quadratic equation, an equation where
x2
is the highest coefficient
and
the lowest is
x0,
cannot be solved using factoring.
When this happens, another way to solve the equation is the quadratic formula.
The quadratic formula is:
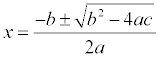
when the equation is in the form ax2+bx+c=0.
To solve, you would then plug a, b, and c into the equation and solve for x. You should be careful and remember the plus-minus and remember the equation must be equal to zero!
Because the quadratic function's graph is in the shape of a parabola, it can have 0, 1, or 2 real roots. This is why a plus-minus is included in the formula. (b^2-4ac) is known as the discriminant. When the discriminant is positive, there are two real roots. When it is negative, there are no real roots. And when it is 0, there is one real root. The discriminant can be used to understand if real roots exist for the function and if solving with the quadratic formula is the best method.
Formula
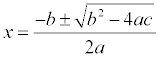
A classic quadratic equation is an equation of the form Ax2 + Bx + C.
{`
Example A: x2 + 2x + 1 = 0
Example B: x2 - x - 2 = 0.
`}
It isn't always easy to solve for x in this case, but there are tricks. The best way is to factor the equation. In case A we can split it up into (x+1) (x+1) =0. Do you see how this works out?
This can be rewritten as (x+1) 2 = 0. We can then square root both sides: √[ (x+1) 2] = √(0) and then
x+1=0
Now that's an equation we know how to solve. x = -1.
In case A there was only one possible value for x, but in general there are two possibilities. Notice how we can rewrite B as (x-2) (x+1) =0. If I asked you when this is zero, you'd say, 'well if x is positive two then the (x-2) term is zero and zero times (x+1) is also zero. Therefore, positive two must be one possibility. Also, if x=-1 then (x+1) =0 so x=-1 is the second.
Example 1 of Solving Quadratic Equation
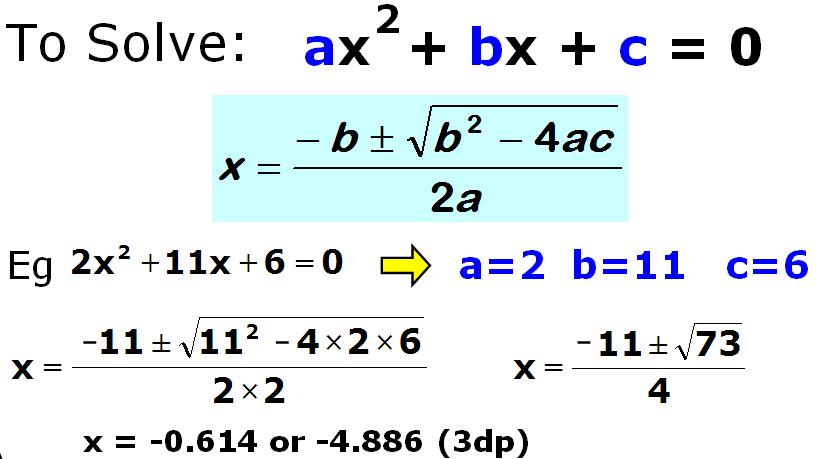
Example 2 of Solving Quadratic Equation
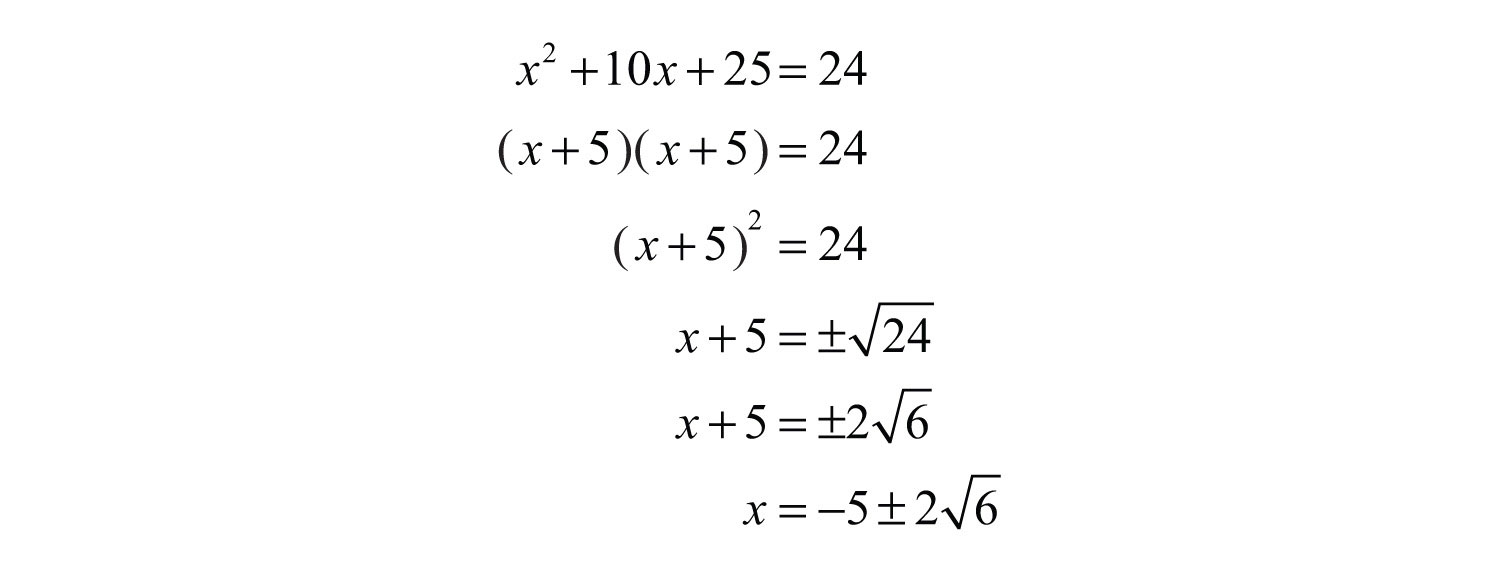
Math Tutorials
- Math - Polynomials
- Math - Series and Sequences
- Math - Dividing Polynomials
- Math - Factoring Polynomials
- Math - Solving Quadratics
- Math - Solving Inequalities
- Math - Solving Equations
- Math - Complex Numbers
- Math - Matrix
- Math - Inverse Functions
- Math - Graphing Quadratic Functions
- Math - Graphing Polynomial Functions
- Math - Functions
- Math - Exponentials and Logarithms
- Math - Cramer's Rule
- Math - Absolute Value & Inequalities

