Natural Number and Induction Homework Help

1. Show all steps in calculating that 2.(1+3)=8 including justification of each step. Do not use any laws of arithmetic. Only use the definitions of addition and multiplication, together with abbreviations.

2. Prove that for all natural numbers n,

1+2+4+8+...+2ⁿ+1=2ⁿ⁺¹.

(8 points)

3. Prove by induction on k that for every natural number k, there are natural numbers m and n, so that

2.k=(m+n).(m+n+1)+2.n.

(10 points)

4. The Fibonacci function is defined by the following recursion.

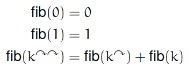
1. Construct a table of the first 10 values of fib(n).
2. Show that for every natural number n,

fib(2n+2)+fib(n)²=fib(n+2)²

and

fib(2n+1)+fib(n)²=fib(n+1)²

In these problem, we consider lists consisting only of natural numbers.

(10 points)

5.

1. We want to define the sum of such a list to mean the obvious thing: Σ([2,3,4])=9. Write a formal recursive definition of Σ(K).
2. Using your definition, prove that for any two lists of natural numbers, Σ(K+L)=Σ(K)+Σ(L).

Sets and Functions

Note: A function f: {'X->Y'} is onto if it is the case that for every b∈Y there is at least one a∈X so that f(a)=b. A function is one-to-one if it is that case that for every b∈Y, there is at most one a∈X so that f(a)=b.

6. Consider the sets {'A={0,1,2,3}'}and {'B={a,b,c}'}.

1. Write out the set B X A using correct notation.
2. Draw a picture of a function from A to B that is not a bijection (not a matching).
3. Is there a bijection between A and B. Explain your answer.
4. How many functions are there from B to A? Explain your answer.
5. How many onto functions are there from B to A.

(8 points)

7.

1. Given two sets C and D for which C X D is equal to D X C.
2. Show that for any two sets A and B, it is the case that there is a bijection from A X B to B X A.

(6 points)

8. Suppose you are given following functions: {'f:N->N,g:N->N and N->N'} defined by

f(m)=m₂

g(m)=m+1

h(m)=2.m

1. Using composition only (that is, by writing expressions like g o g o h), define new functions that calculate the following

{'m->m'}⁸+4

{'m->2m'}²+3

{'m->m'}⁴+4m₂+4

{'m->4m'}²+4m+1

2. Is it possible to define {'m ->m'}₃ using composition and these three functions ? Explain why or why not.

(8 points)

9. We write A ∼ B to mean that A and B are the same size (have the same cardinality). Write a clear and rigorous definition of what A ∼ B means in terms of functions. Do not give examples. Just write a mathematical definition

(6 points)

10.

1. For sets A and{' B = {0,1}'}, define a one-to-one function {'F:A->B'}_A.
2. Show that F is not also onto.
3. Show that three is no onto function from A to B_A.

(12 points)

11. We say that a set is countable if there is a one-to-one function {'f:A->N'}. We say that a set is denumerable if there is an onto function {'g:N->A'}.

1. Show that every denumerable set is countable.
2. Show that every non-empty countable set is denumerable.

(10 points)

Math Tutorials

Math - Polynomials

• Math - Series and Sequences
• Math - Dividing Polynomials
• Math - Factoring Polynomials
• Math - Solving Quadratics
• Math - Solving Inequalities
• Math - Solving Equations
• Math - Complex Numbers
• Math - Matrix
• Math - Inverse Functions
• Math - Graphing Quadratic Functions
• Math - Graphing Polynomial Functions
• Math - Functions
• Math - Exponentials and Logarithms
• Math - Cramer's Rule
• Math - Absolute Value & Inequalities

Math University Question

• Natural Number and Induction Homework